面板数据进行熵值法

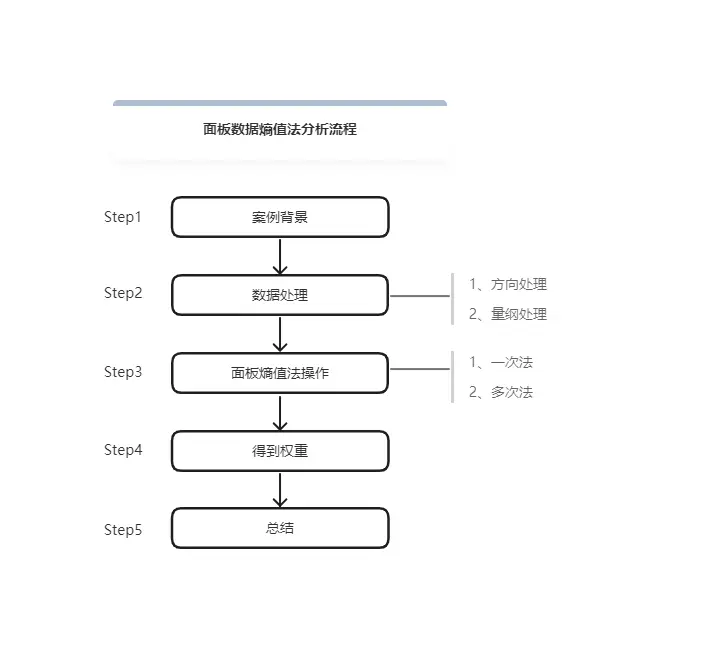
面板数据熵值法分析流程如下：

一、案例背景

当前有9家公司连续5年（2018-2022年）的财务指标数据，想要通过这份数据，确定各个财务指标的权重。熵值法根据指标离散程度确定赋权大小，客观公正准确度高。本次收集的指标数据不多，选择熵值法确定指标权重具有很强的操作性，运算过程简单易操作。

数据为9家公司连续5年的5个财务指标的数据，因为同时包含时间序列数据和截面数据，所以属于面板数据。应该有9*5=45行数据，5个财务指标各占一列，同时公司编号和年份各占一列，最后应该为45行*7列数据，最终应该将数据整理为如下格式：

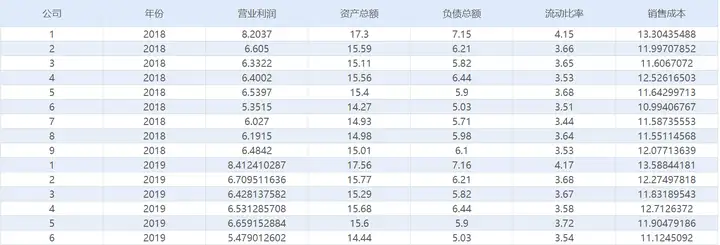
数据虚构，仅做教学演示

二、数据处理

使用熵值法进行分析，需要对数据进行处理，包括数据方向处理和数据量纲处理。

（1）方向处理

本次分析的5个指标分别为营业利润、资产总额、负债总额、流动比率、销售成本。可以看出，这5个指标既有正向指标（越大越好的指标，如利润），又有逆向指标（越小越好的指标，如成本）。熵值法的运算规则中，正向指标越大越好，逆向指标越小越好，所以需要对数据进行方向处理。

将正向指标“营业利润”、“资产总额”、“流动比率”使用SPSSAU进行正向化处理；将逆向指标“负债总额”、“销售成本”使用SPSSAU进行逆向化处理。

SPSSAU【生成变量】->正向化/逆向化->确认处理，操作如下图：

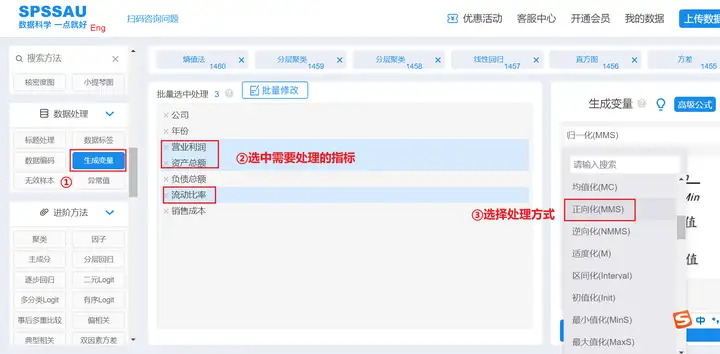
同理，将其他两个指标进行逆向化处理即可。

（2）量纲处理

熵值法消除数据方向的影响后，还需要消除由于数据单位不同造成的影响，即进行量纲处理，SPSSAU提供十几种量纲处理方法，这里推荐使用数据归一化进行处理。

本案例因为上述分析中已经进行了正向/逆向此两种处理，而正向/逆向化处理可同时解决方向和量纲问题，所以不需要再次进行归一化处理。数据处理完成之后，接下来进行面板熵值法操作说明。

三、面板熵值法操作

熵值法是根据熵值进行权重确定的。“熵”原本是热力学的概念，后来被引入到信息论中，用于客观确定权重。熵值原理是通过指标的离散程度判断权重大小，离散程度越大说明不确定因素越多，对评价结果影响越大，权重越大。

从熵值的计算原理上看，并不会考虑是否为面板数据，面板数据与普通数据完全一致，直接放入分析即可。

从分析角度来看，针对面板数据，可以从两个角度进行熵值法分析，说明如下表：

接下来分别使用两种方法进行面板数据熵值法操作说明。

（1）一次法

在SPSSAU系统中，综合评价【熵值法】->将处理后的数据全部拖拽到分析框中->非负平移->开始分析

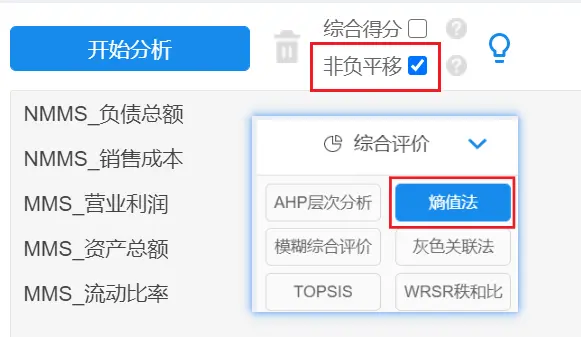
此时得到权重即为不区分是否面板数据，直接一次进行熵值法计算得到的指标权重。

补充非负平移：经过正向化/逆向化/标准化处理的数据，指标数据范围可以取到0，但是计算熵权时会进行取对数计算，出现0会导致计算无意义，所以需要对整体数据进行非负平移。SPSSAU非负平移功能是指，如果某列（某指标）数据出现小于等于0，则让该列数据同时加上一个“平移值”【该值为某列数据最小值的绝对值+0.01】，以便让数据全部都大于0，从而满足算法要求。

（2）多次法

分别筛选出2018-2022年的数据，进行5次熵值法，然后将得到的5次权重值进行取平均值的操作。

SPSSAU筛选操作如下：

筛选年份后，与一次法操作相同，分别进行5次熵值法，得到权重值，然后取平均值。

四、得到权重

（1）一次法权重计算结果

“一次法”进行面板数据熵值法得到权重结果如下：

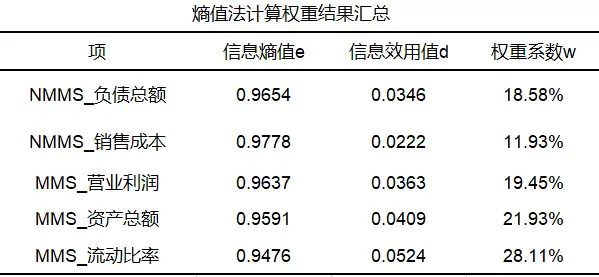
使用熵值法对NMMS_负债总额等总共5项进行权重计算，从上表可以看出5个指标的权重值分别是18.58%、11.93%、19.45%、21/93%、28.11%。

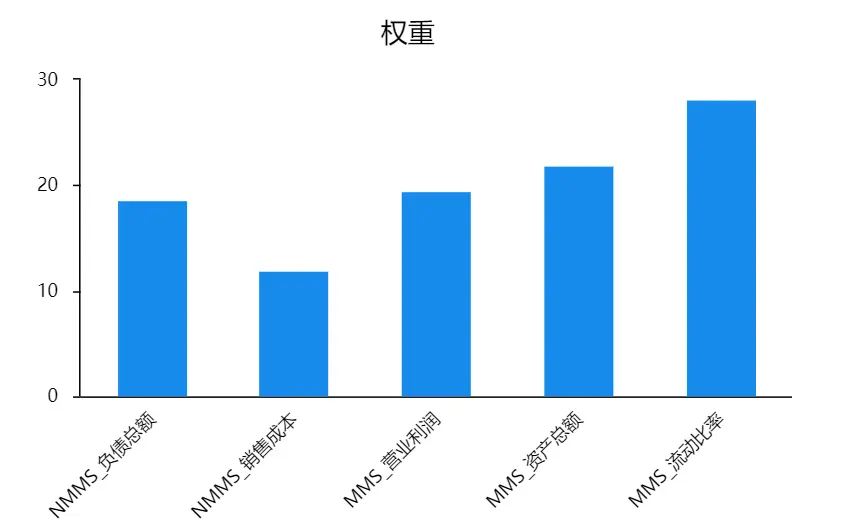
SPSSAU输出权重可视化结果如下图：

（2）多次法权重计算结果

“多次法”进行面板数据熵值法，得到权重汇总结果如下表：

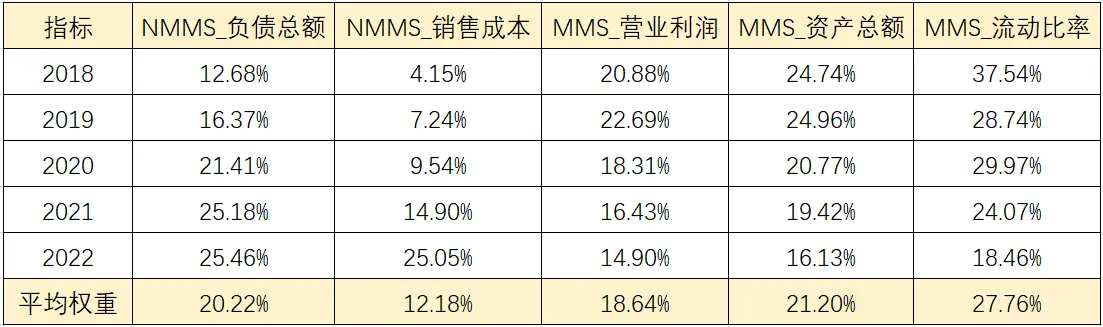
“多次法”进行熵值法，得到5个指标的权重值分别为37.54%、28.74%、29.97%、24.07%、18.46%、27.76%。

两种方法进行面板数据熵值法得到权重值对比见下表，可以看出两种方法计算面板数据的熵值法，得到的指标权重值接近。

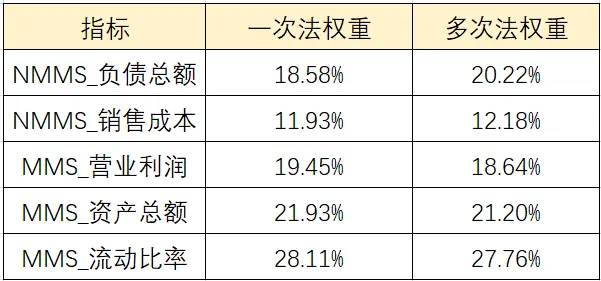
提示：“多次法”进行面板数据熵值法分析，从原理上可行，此种做法是出于分析考虑，考虑了不同年份时数据的波动差异性。

五、总结

面板数据进行熵值法，与普通数据进行熵值法类似。首先需要统一数据方向，对正向指标进行正向化处理、逆向指标进行逆向化出理。如果数据单位不一致，需要消除量纲的影响，进行数据标准化处理。但是数据经量纲处理后，很可能出现负值，熵值法计算过程中包括取对数的操作，所以需要对数据进行非负平移，以确保分析结果能顺利得出。

面板数据进行熵值法有两种方法可以选择，分别是“一次法”和“多次法”。一次法不考虑是否面板数据，与普通数据一样做一次分析即可；多次法按年份分析，分别求出每一年指标的权重，然后取平均值。两种方法进行面板数据熵值法得到的指标权重值接近，多次法考虑了不同年份数据的波动差异性，两种方法研究人员可以自行选择来进行面板数据熵值法分析。