回归分析有多少种?
在进行自变量X与因变量Y的影响关系研究时,大家第一反应都大概知道需要进行回归分析,但是回归分析的方法有很多种,常用的回归分析方法有哪些?各种回归分析方法之间的区别是什么?应该怎样选择最合适的回归分析方法呢?
今天一文将回归分析方法相关知识进行说明。
1、回归分析方法
回归分析简单来讲就是用于分析自变量X与因变量Y之间的影响关系的方法。回归分析主要基于自变量X的值预测因变量Y的值,通过构造回归模型,帮助理解自变量如何影响因变量,以及各个自变量对因变量的影响程度。
SPSSAU中回归分析方法可分为以下二十种:
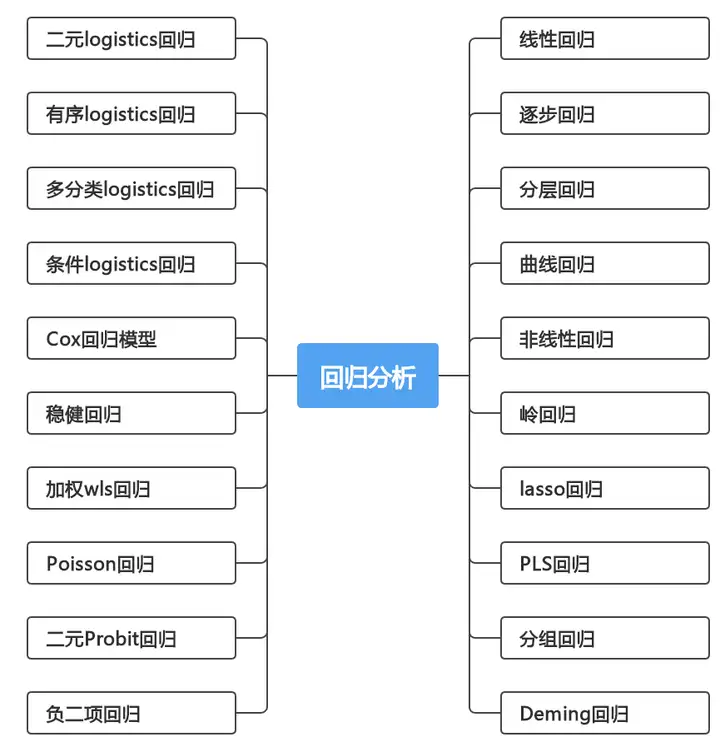
为什么会有如此多的回归分析方法?
在研究X对于Y的影响时,会区分出很多种情况,比如因变量Y的数据类型,可能是定类数据也可能是定量数据;Y的个数有多个或者1个。同时每种回归分析还有很多前提条件,如果不满足则有对应的其它回归方法进行解决。这也就解释了为什么会有如此多的回归分析方法。
那么面对如此多种类回归分析方法,该如何快速选择最合适的方法进行回归分析呢?
2、回归模型选择
论文写作用中回归模型的选择,一般需要结合自变量和因变量的个数以及数据类型进行判断。
(1)数据类型
数据分为两类:定类数据和定量数据
简单进行区分:看数字大小是否具有比较意义
定量数据:数字大小具有比较意义
例如:GDP、身高、体重、工资、量表题选项(1,2,3,4,5)等等
定类数据:数字大小仅代表分类,不具有比较意义
例如:性别(1和0分别代表男和女,不具有比较意义)、学历、职位等
(2)回归分析方法初步判断
回归分析方法初步判断方法如下:
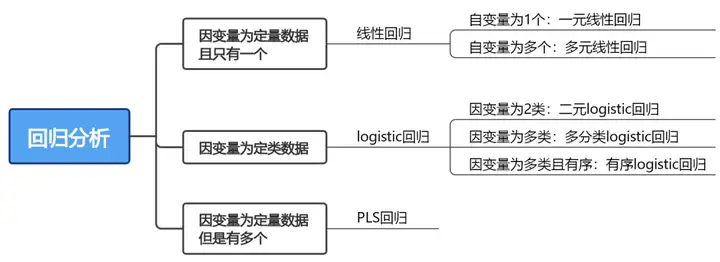
第一步:首先判断因变量类型
当因变量为定量数据且只有1个时,一般使用线性回归进行分析;
当因变量为定量数据且有多个时,可以使用PLS回归进行分析;
当因变量为定类数据时,一般常用logistic回归进行分析。
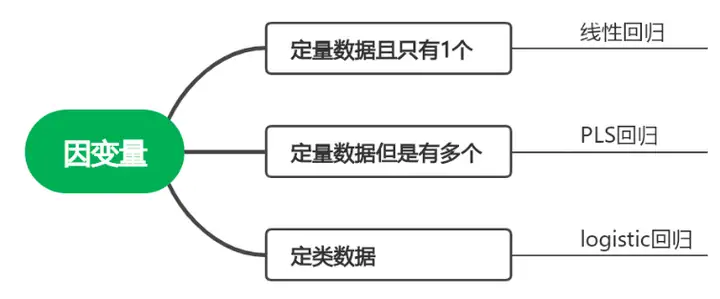
第二步:若判定为线性回归,看自变量个数
自变量为1个时,选择一元线性回归分析;
自变量为多个时,选择多元线性回归分析。
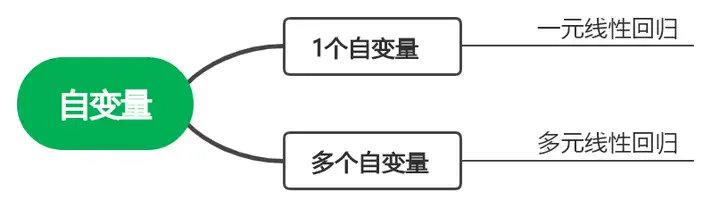
第三步:若判定为logistic回归,看因变量
因变量为2类,比如男&女、苹果&安卓、阳性&阴性,选择二元logistic回归分析;
因变量为多类,比如学科数学、语文、英语、物理,选择多分类logistic回归分析;
因变量为多类且有序,比如不满意、一般、满意,选择有序logistic回归分析。

以上为比较常见的回归分析方法选择的一般步骤,其中提到的回归方法都是在实际研究中使用频率较高的。
(3)深入分析线性回归模型
线性回归模型是当前使用最为成熟,研究最多的回归分析方法之一。线性回归模型会有很多假定,或者需要满足的条件,如果不满足这些假定或者条件可能会导致模型使用出错,分析结果存在偏差等问题出现,那么此时就有对应的其它回归模型出来解决这些问题,因而跟着线性回归后面又出来很多其他回归分析方法,如下图:
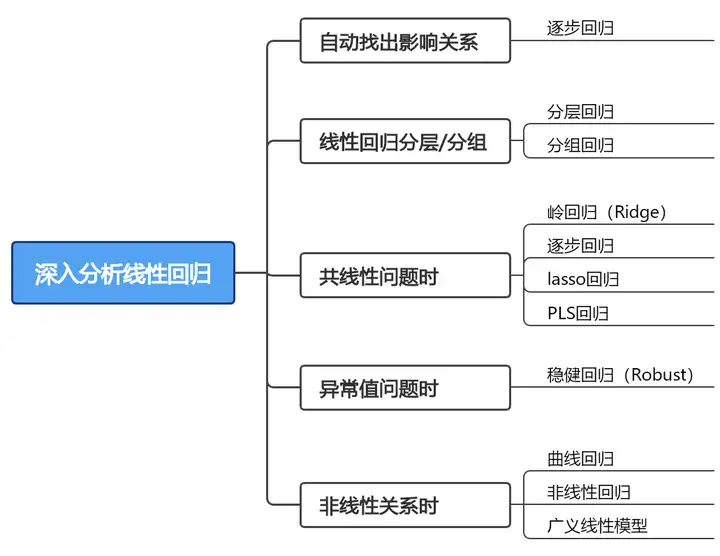
1、自动找出影响关系
多元线性回归研究多个自变量X对因变量Y的影响,当希望让模型自动找出对Y有意义的X时,此时可以使用逐步回归进行分析。逐步回归分析可以查看下方帮助手册说明:
2、线性回归分组/分层
在进行中介作用或者调节作用分析时,可能会用到分层回归或者分组回归。分层回归可以得出:分层a到分层b(b=a+1)时R方变化和F值变化,便于观察加入新的X时回归模型的变化信息等。分组回归的实质目的在于查看不同组别时,X对于Y的影响差异。
3、共线性问题时
在进行线性回归时,如果出现共线性问题时,可以使用岭回归、逐步回归进行分析。lasso回归和PLS回归也可以在一定程度上解决共线性问题,但是用较少,通常岭回归使用比较广泛。
4、异常值问题时
当数据中存在异常值时,通常需要将异常值剔除后再进行回归分析,但是当不能将异常值剔除,需要将异常值考虑在模型中时,此时可以使用稳健回归(Robust回归)进行分析。稳健回归会对不同点的残差给予不同权重,异常点的残差值会比较大,因为其对应的权重会很小,最终拟合出的结果也更加稳健可靠。
5、非线性关系时
线性回归模型使用的前提条件是X与Y之间存在线性关系(可在分析前通过散点图查看),但是有时二者并不是线性关系,此时可以选择使用曲线回归、非线性回归、广义线性回归三类回归分析进行研究。
- 曲线回归:
曲线回归在关系形式上是非线性关系,但可通过各类转换变成线性关系,最终建立回归模型。比如建立二次曲线拟合,最终模型表达式为:y = β0+β1*x+β2*x2 ;SPSSAU当前提供7类曲线拟合模型,详情请查看下方帮助手册说明。
- 非线性回归
如果数学模型为非线性模型,需要使用非线性回归进行分析。比如人口学增长模型Logistic(S模型),其模式公式为:y = b1 / (1 + exp(b2 + b3 * x)),此数学表达式并非线性表达式,因此不能使用SPSSAU的线性回归进行拟合。
SPSSAU当前提供约50类非线性函数表达式,涵盖绝大多数非线性函数表达式。
- 广义线性模型
广义线性模型是对一般线性模型的扩展。将因变量分布由正态分布推广到指数一族分布,应用范围更广了。常见的广义线性模型有Possion回归、负二项回归、logistic回归、Probit回归等。
3、回归分析操作和分析
以多元线性回归分析为例,使用SPSSAU进行操作和分析演示。
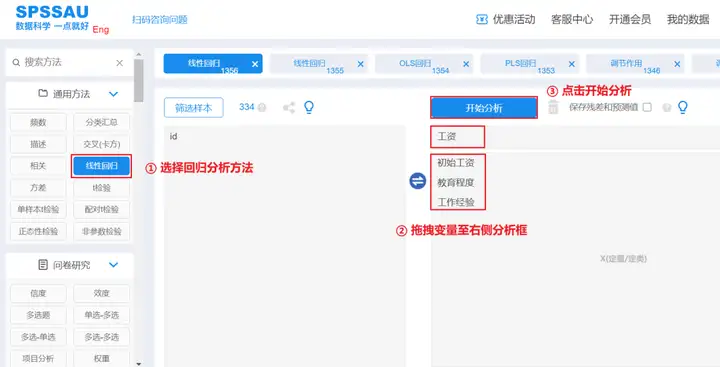
(1)操作
选择分析方法->拖拽数据至右侧分析框->点击开始分析
(2)分析
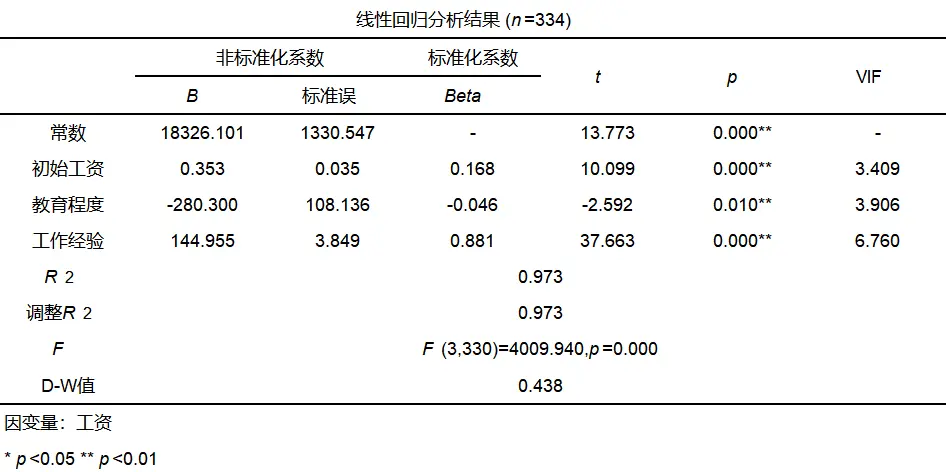
SPSSAU输出结果线性回归分析结果如下:
多元线性回归模型分析一般可分为以下几步:
① 对模型基本情况进行分析
模型总体显著性—F检验:用于判定是否X中至少有一个对Y产生影响,如果呈现出显著性,则说明所有X中至少一个会对Y产生影响关系。
从上表来看,F检验对应p值=0.000<0.01,说明呈现出显著性,即模型构建是有意义的,至少有1个X会对Y产生影响关系。
模型拟合情况—R方:R方的值介于0~1之间,代表模型的拟合程度,一般认为越大越好。R方为0.3,则说明所有X可以解释Y30%的变化原因。
从上表来看,R方为0.973,说明所有X可以解释Y97.3%的变换原因,模型拟合较好。
模型共线性问题—VIF值:共线性是指在线性回归分析时,出现的自变量之间彼此相关的现象。一般VIF值大于10(严格大于5),则认为存在严重的共线性。
从上表来看,VIF值均小于10,可以认为不存在共线性问题。
② 分析自变量X的显著性
自变量X的显著性通过t检验进行判断,如果X对应t检验的p值小于0.05说明具有显著性,即该自变量会对因变量产生显著影响。
从上表来看,“初始工资”、“教育程度”、“工作经验”对应t检验的p值均小于0.05,说明这3个自变量均会对因变量“工资”产生显著影响。
③ 判断自变量对因变量的影响大小和影响方向
自变量对因变量影响大小的比较是通过标准化回归系数进行比较的。标准化回归系数的绝对值越大,说明该自变量对因变量的影响越大;回归系数的正负代表影响方向。
从上表来看,“初始工资”、“教育程度”、“工作经验”的标准化回归系数分别是:0.168、-0.046、0.881;所以工作经验对工资的影响最大,其次是初始工资,影响最小的是教育程度,且初始工资与工作经验对工资的影响是显著正向的,而教育程度对工资的影响是显著负向的。
④ 回归模型公式
构建回归模型使用非标准化回归系数,它是方程中不同自变量对应的原始回归系数,反映了在其他自变量不变的情况下,该自变量每变化一个单位对因变量作用的大小。通过非标准化回归系数构建的回归方程,才可以对因变量进行预测。
从上表来看,回归模型公式为:工资=18326.101 + 0.353*初始工资-280.300*教育程度 + 144.955*工作经验。




