二元logistic回归分析
二元logistic回归分析流程如下图:
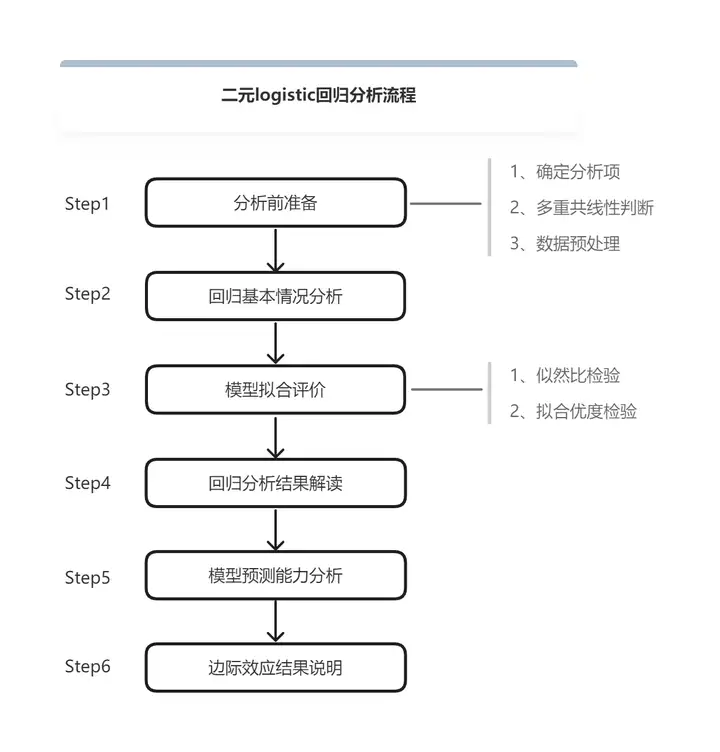
一、分析前准备
二元logistic回归分析适用于研究因变量为二分类变量的数据,二分类变量即为那些结局只有两种可能性的变量。比如因变量表示为“是”或“否”、“同意”或“不同意”、“发生”或“不发生”这类形式。
当前有一份数据,想要分析在银行贷款的客户其“是否违约”的影响因素,当前掌握的可能影响因素有年龄、工资、教育水平、负债率、信用卡负债、工作年限、居住时长。
在进行二元logistic回归分析之前,需要进行一些准备工作,来提高分析结果的准确性。准备工作包括进行分析项即自变量的确定、多重共线性判断、以及变量处理三方面,接下来将逐一进行说明。
- 确定分析项
因为影响因素比较多,并不能确定单个影响因素是否会对“是否违约”这一因变量产生影响,为了筛选确实对因变量有影响的自变量进行分析,可以在进行二元logistic回归分析之前就单个因素的影响情况进行分析(非必要步骤)。根据影响因素类型不同,可以分别进行方差分析(t检验)、卡方检验进行分析。
1.1 连续变量方差分析
对于年龄、工资、负债率、信用卡负债、工作年限、居住时长这类影响因素,都是连续型变量,研究此类变量与“是否违约”的关系情况可以使用方差分析进行分析。
使用SPSSAU进行方差分析得到分析结果如下:
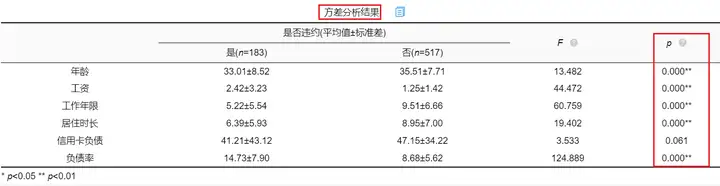
从方差分析结果来看,违约客户与未违约客户的信用卡负债情况并没有呈现出显著性差异(p=0.061>0.05),其余变量都呈现显著性差异。所以,可以将信用卡负债率这一影响因素在后续分析中剔除(如果担心遗漏重要变量,也可以将显著性水平放宽至0.1)。
- 分类变量卡方检验
对于教育水平这一分类变量,研究其与“是否违约”的关系情况可以使用卡方检验。
使用SPSSAU进行卡方检验得到分析结果如下:

从卡方检验结果来看,不同教育水平的客户其“是否违约”情况呈现出显著性差异(p=0.。022<0.05),对该变量予以保留。
确定好分析项之后,需要考虑回归分析的多重共线性问题。
2.多重共线性判断
对于因变量为二分类变量的模型的多重共线性判断,也可以使用线性回归方法进行简单查看。使用SPSSAU进行线性回归分析结果如下:

从上表可以看出,VIF值均小于5,说明模型并不存在共线性问题。如果存在共线性问题可使用岭回归或者逐步回归进行解决。接下来进行下一步分析,进行二元logistic回归分析前的数据预处理。
3.数据预处理
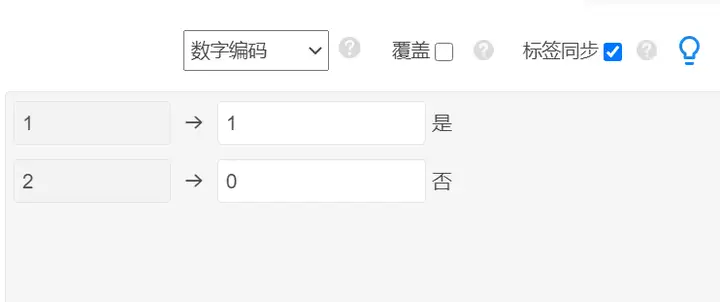
3.1 因变量0-1编码
二元logistic回归分析要求因变量必须用数字0、1进行编码,即“是”用1表示,“否”用0表示。可以使用SPSSAU数据编码进行操作,因为原始数据使用数字1表示“是”,数字2表示“否”,现在需要重新编码为数字1表示“是”,数字0表示“否”,见下图:
3.2 分类自变量哑变量处理
二元logistic回归分析中自变量既可以是定量数据也可以是分类数据,如果是分类数据需要进行哑变量处理,在分析时将生成的哑变量少放一项,作为参考项。由于“教育水平”为分类数据,所以需要进行哑变量处理,生成的哑变量如下图:

在进行分析时,对于教育水平5个哑变量,需要保留一项作为对照项,不放进分析框中。比如将“教育水平_大专”作为对照项,则不将该哑变量放入分析框中,将剩下的四类教育水平放进分析框中。
分析前准备到此就结束了,接下来进行二元logistic回归分析的主体部分,使用SPSSAU进行二元logistic回归分析。
二、回归基本情况分析
二元logistic回归分析得到的第一个表格为二元logit回归分析基本汇总,见下表:

上表对于分析数据的基本情况进行了说明;包括因变量“是否违约”的数据分析和最终分析有效样本量的数据情况。可以看出,总共有850个样本参加分析,但模型分析时共剔除掉缺失数据为150个,参加分析的样本有效率为:82.4%(如果缺失数据过多,或者Y值分布非常不均匀,可能会导致模型质量较差)。
回归基本情况分析可以对数据有一个整体的感知,一般来讲并没有非常大的意义。接下来,进行模型拟合评价。
三、模型拟合评价
二元logistic回归分析的模型拟合情况判断可以分为两类,分别是似然比检验和Hosmer-Lemeshow拟合度检验两种。
- 似然比检验
似然比检验用于对整体模型的有效性进行检验,SPSSAU输出的二元logistic回归模型似然比检验结果如下图:

从上图可以看出,似然比检验的p值小于0.05,说明模型是有效的,反之说明模型无效。AIC值和BIC值是回归分析中选择模型的两条重要准则,这两个值都是越小越好的。在进行多次对比选择模型时,可以结合这两个值的变化,说明模型构建的优化情况。其余值为中间计算过程值,无其他意义。
- 拟合优度检验
当模型的总体有效后,接下来具体分析哪些自变量会对因变量产生显著影响。

Hosmer-Lemeshow拟合度检验用于判断模型拟合优度。p值大于0.05则说明通过HL检验,反之则说明模型没有通过HL检验,模型拟合优度差。从上表可知:检验对应的 p值大于0.05,说明本次模型通过HL检验,模型拟合优度较好。
四、回归分析结果解读
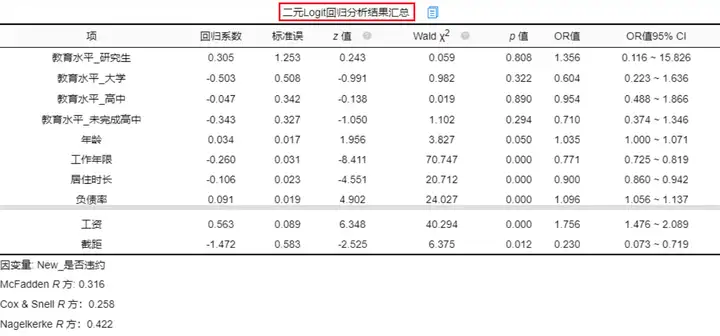
二元logistic回归分析结果如下图:
1.R方值分析
表格下方会提供此3个R方值,此3个R方均为伪R方值,其值越大越好,但其无法非常有效的表达模型的拟合程度,意义相对交小,而且多数情况此3个指标值均会特别小,一般而言,伪R方值一般达到0.2以上就表示具有较好的拟合优度,但是如果在实际应用中是侧重影响因素分析,则可以不需要太注重这个指标,只要分析系数的显著性即可。
2.模型公式
从上表可知:模型公式为:ln(p/1-p)=-1.472 + 0.305*教育水平_研究生-0.503*教育水平_大学-0.047*教育水平_高中-0.343*教育水平_未完成高中 + 0.034*年龄-0.260*工作年限-0.106*居住时长 + 0.091*负债率 + 0.563*工资
(其中p代表New_是否违约为1 的概率,1-p代表New_是否违约为0的概率)。
3.X对Y影响情况分析
查看9个自变量对应的p值,可以得到,4种教育水平、年龄并不会对“是否违约”产生显著影响关系(p值均大于0.05);工作年限、居住时长、负债率和工资会对“是否违约”产生产生显著影响。其中,工作年限和居住时长会对违约情况产生显著负向影响,即工作年限和居住时长越长,越可能出现违约情况。而负债率和工资会对违约情况产生显著的正向影响,即负债率越高、工资越高,越不会出现违约情况。
4.OR值说明
OR值(odds ratio)又称比值比、优势比。
上图Logistic回归分析结果输出的OR值,工作年限会对“是否违约”产生显著的负向影响关系,优势比(OR值)为0.771,意味着工作年限增加一个单位时,“是否违约”的变化(减少)幅度为0.771倍;工资会对“是否违约”产生显著的正向影响关系。优势比(OR值)为1.756,意味着工资增加一个单位时,“是否违约”的变化(增加)幅度为1.756倍。
回归分析结果可以参考SPSSAU的智能分析结果进行说明。

回归分析除了研究自变量对因变量的影响情况,还可以实现预测。接下来,进行模型预测能力分析。
五、模型预测能力分析
SPSSAU会输出模型预测准确率,见下图:

通过模型预测准确率去判断模型拟合质量,从上表可知:研究模型的整体预测准确率为81.71%,模型拟合情况可以接受。当真实值为0(不违约)时,预测准确率为92.46%;另外当真实值为1(违约)时,预测准确率为51.37%。
实际研究中,我们更关注预测“违约=1”的准确率,所以本次分析中预测准确率是很低的。如果实际研究中,数据预测准确率很低,比如低于85%,此时可以考虑删除部分X,或者多次进行二元logistic回归分析进行对比结果,选出最优的模型结果。
代入数据进行预测:比如想要预测年龄为35岁、教育水平为未完成高中、工资为3万、工作年限为2年、居住时长为2年、负债率为0.6的用户是否违约情况,操作如下图:

预测得到该用户违约的概率是0.596,说明该用户未来违约的概率较高。
SPSSAU还会在分析时同时输出边际效应情况,
六、边际效应结果说明
“边际效应指的是在其他一切条件不变的情况下,一种要素的供给量持续增加,达到一定程度之后,它所产生的作用将会下降,即可变因素的边际效应会发生递减。”
如果自变量对应的边际效应检验值的p值小于0.05,说明该变量有着显著的边际效应;反之则说明该变量没有显著的边际效应。如果边际效应值显著且大于0,则意味着该变量的增加会带来正向效应变化,如果边际效应值显著且小于0,则意味着自变量的增加时带来负向效应变化。
SPSSAU输出均值处的边际效应值及对应的检验及95%置信区间值等,见下图:

从上图可以看出,工资、负债率的增加会带来显著的正向效应变化,而工作年限和居住时长的增加会带来显著的负向效应变化。
二元logistic回归分析的的流程到此为止就全部结束了,在使用该方法时一定要注意,因变量的数据类型是二分类变量,并且进行0-1编码;同时分类自变量需要进行虚拟哑变量设置,在分析时留一项作为对照项,否则无法进行分析。




