量纲化处理汇总
在实际研究中，不同的变量单位不同，数值差异极大。例如100g和1m等。 因此有时需要对数据进行去量纲，所谓的去量纲就是‘去掉’单位对数值的影响。但是量纲化有很多种方式，但具体应该使用哪一种方式，并没有固定的标准，而应该结合数据情况或者研究算法，选择最适合的量纲化处理方式，SPSSAU共提供12种量纲化处理方法，下面进行说明。
一、利用SPSSAU进行量纲化操作
量纲化处理应该如何操作？以SPSSAU为例，量纲化处理在SPSSAU的数据处理板块，具体位置在SPSSAU【数据处理】→【生成变量】处；
二、量纲化处理分类
量纲化有很多种处理方式，其中常见的处理为12种，SPSSAU均有提供，可以将12种方法分为两大类，一类为‘有实际意义的量纲处理’另一类为‘数理化的量纲处理’。接下来对两类量纲化处理分别进行说明。
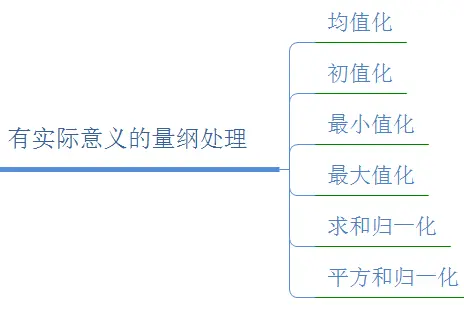
1.有实际意义的量纲处理
有实际意义的量纲处理包括均值化、初值化、最小值化、最大值化、求和归一化和平方和归一化。接下来一一进行描述。
（1）均值化：
均值化在综合评价时有可能使用，比如进行灰色关联法研究时就常用此种处理方式；其计算公式是以平均值作为单位，全部数据均去除以平均值。但是并不是所有数据都能进行均值化处理，一般需要数据均大于0。
那么如何判断自己的数据是否大于0？如果数据过少可以直接通过观察进行判断，但是如果数据量很大，不好观察，可以通用SPSSAU中【通用方法】的【描述】进行观察。
（2）初值化
什么是初值化？使用序列数据中的初始值作为除数，消除不同变量之间的量级或单位差异。其计算公式为X / 该列第1个不为空的数据,以第一个不为空的数据作为参考，其余全部除以该值，例如：
一般来说，初值化这种处理方式适用于有着一种趋势或规律性的数据，而且数据正常情况下都是全部大于0，因为出现负数，通常会失去其特定意义。
（3）最小值化
最小值化，其目的是让最小值作为参照标准，所有的数据全部除以最小值；此种处理方式时一般都是要求数据全部大于0，否则可能就不适合用此种量纲方式。
（4）最大值化
最大值化，其目的是让最大值作为参照标准，所有的数据全部除以最大值；此种处理方式时一般都是要求数据全部大于0，否则可能就不适合用此种量纲方式。
（5）求和归一化
求和归一化，其目的是让‘求和值’作为参照标准，所有的数据全部除以求和值，得到的数据相当于为求和的占比。
主成分计算综合得分以及Topsis法应用比较多。一般要求数据都大于0。
（6）平方和归一化
平方和归一化所有数据全部除以平方和值。
Topsis法应用比较多。一般要求数据都大于0。
补充说明：使用‘有实际意义的量纲处理’即均值化，初值化，最小值化，最大值化，求和归一化，平方和归一化。一般都输需要数据大于0，否则很可能会失去其意义。
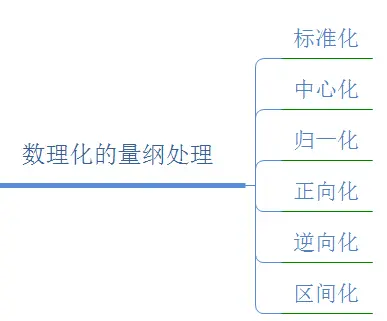
2.数理化的量纲处理
（1）标准化
标准化是一种最为常见的量纲化处理方式。其计算公式为：（X-Mean）/ Std。让数据的平均值变成0，标准差变为1（标准化后，虽然数据满足了正态分布的某些特征，比如均值为0，方差为1，但是数据分布同原数据分布），因为标准化处理针对量纲引起的差异去除的更为彻底一般对于距离计算中，使用此方法效果更好。比如聚类分析时，其内部算法原理在于距离大小来衡量数据间的聚集关系，因此进行标准化处理。
SPSSAU系统中对于聚类分析、主成分以及因子分析默认使用标准化处理。
（2）中心化
针对数据进行了压缩大小处理，让数据的平均值为0。其计算公式为：X - Mean。一般社会学等使用的比较多。
（3）归一化
归一化的目的是让数据压缩在【0，1】范围内，其中也包括0和1；其计算公式为（X - Min）/ (Max - Min)。归一化几乎适用于所有场景，但是如果最大最小值不稳定，其归一化结果也不稳定，可能会导致后续使用归一化数据分析的效果也不稳定。
（4）正向化
在实际研究中有的指标是越大越好，此时为正向指标，需要正向化，对正向指标保持正向且量纲化。并且也将数据压缩在【0，1】。
（5）逆向化
在实际研究中有的指标是越小越好，此时为逆向指标，需要对逆向指标正向且量纲化。便于进行方向的统一，并且也将数据压缩在【0,1】之间。
（6）区间化
区间化的目的是让数据压缩在【a，b】范围内，a和b是自己希望的区间值，如果a=0,b=1，那么其实就是一种特殊情况即归一化；其计算公式为a + (b - a) * (X - Min)/(Max - Min)。
三、实际问题处理
上述已经了解到12种量纲化处理的方式以及量纲化处理的分类，接下来说明量纲化处理如何和实际相联系，解决实际问题？（由于处理方法过多，所以这里以正逆向化处理为说明）
比如这样一些指标GDP增长率、就业率、失业率共3个指标；明显的，GDP增长率、就业率是数字越大越好，而失业率是数字越小越好。所以在分析时可以考虑将GDP增长率、就业率进行正向化处理，将失业率进行逆向化处理。从而便于进行方向的统一。当然还要结合分析方法具体分析。
