灰色预测模型案例分析
在实际生活中，常常要根据现有的经验或者数据做出预测。比如，预测账号粉丝量，年度销售额等等。研究时间序列的主要目的之一就是进行预测。本篇案例讲述用灰色预测模型如何预测啤酒产量。
一、方法说明
灰色预测模型可针对数量非常少，数据完整性和可靠性较低的数据序列进行有效预测，其利用微分方程来充分挖掘数据的本质，建模所需信息少，精度较高，运算简便，易于检验，也不用考虑分布规律或变化趋势等。
二、优缺点
优点：不需要很多数据，就能解决历史数据少、序列的完整性及可靠性低的问题，能利用微分方程来充分挖掘系统的本质，精度高，运算简便，易于检验。
缺点：只适用于中短期预测以及指数增长的预测。
三、案例背景
图中是某工厂1996~2007共12年的啤酒总产量，希望由以往数据预测出往后二期啤酒产量。部分数据如下：
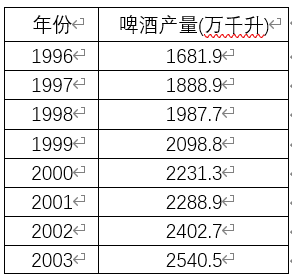
添加图片注释，不超过 140 字（可选）
四、操作
将指标项放入分析框中，点击开始分析。
添加图片注释，不超过 140 字（可选）
默认是进行12期预测，具体预测期数也可以自己填写。
五、结果解释
该案例的使用SPSSAU进行分析，对结果的解释也从4个方面进行，首先说明GM(1,1)模型级比值表格、然后说明后验差比检验结果接着查看模型拟合和预测最后分析模型残差检验。
1.GM(1,1)模型级比值表格
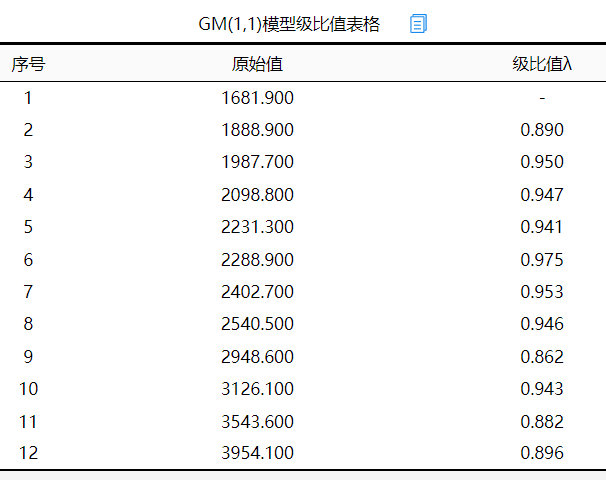
添加图片注释，不超过 140 字（可选）
首先计算级比值，如果在区间[0.857, 1.166]内，
补充说明：区间由【exp(-2/n+1),exp(2/n+1)】计算（n为样本量）。
则说明可用GM(1,1)模型；如果在区间外，可尝试平移变换，也就是给每个数据都加上任意常数c，看是否在区间内；求解后再减去c；
从上表可知，针对啤酒产量(万千升)进行GM(1,1)模型构建，首先进行级比值检验，用于判断数据序列进行模型构建的适用性。级比值为上一期数据/当期数据。结果显示：级比检验值均在标准范围区间[0.857, 1.166]内，意味着本数据适合进行GM(1,1)模型构建 。
2. 后验差比检验
添加图片注释，不超过 140 字（可选）
后验差比C值用于模型精度等级检验，该值越小越好，一般C值小于0.35则模型精度等级好，C值小于0.5说明模型精度合格，C值小于0.65说明模型精度基本合格，如果C值大于0.65，则说明模型精度等级不合格。
从上表可知，后验差比C值0.0321 <0.35，意味着模型精度等级非常好。
3. 模型拟合和预测
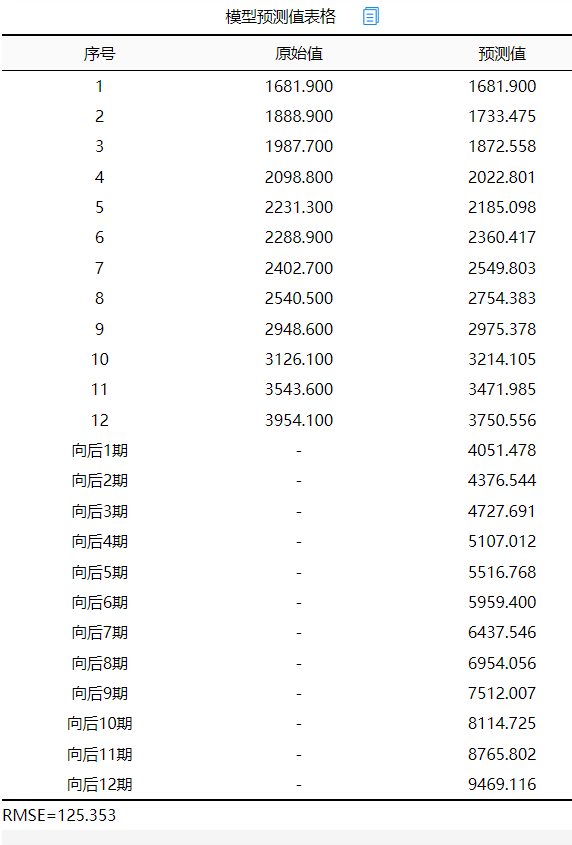
添加图片注释，不超过 140 字（可选）
上表格展示出模型的拟合值，以及向后12期的拟合数据情况，当然也可通过图形直观查看如下图，下图明显可以看出，往后时会一直上升，这是GM(1,1)模型的特征，其仅适用于中短期预测，因此向后1期和向后2期的数据具有价值，更多的预测数据需要特别谨慎对待。
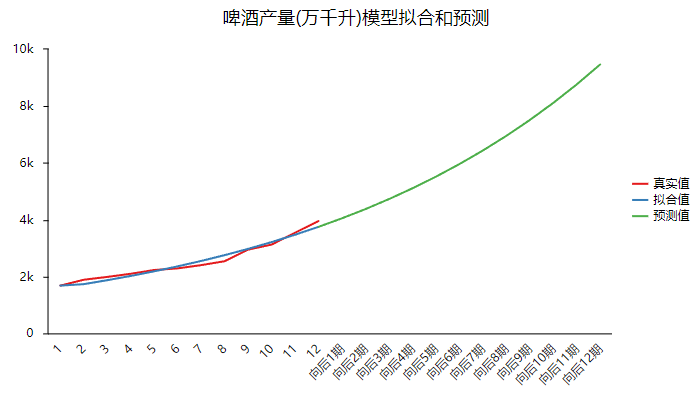
添加图片注释，不超过 140 字（可选）
4.模型残差检验
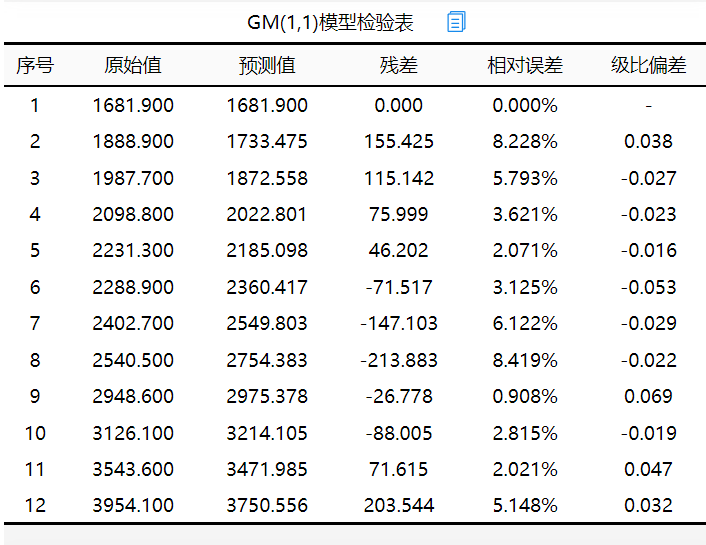
添加图片注释，不超过 140 字（可选）
模型残差检验，主要是查看相对误差值和级比偏差值，相对误差值越小越好，该值小于0.2说明达到要求，小于0.1说明达到较高要求，级比偏差值越小越好，该值小于0.2说明达到要求，小于0.1说明达到较高要求。验证模型效果情况：从上表可知，模型构建后可对相对误差和级比偏差值进行分析，模型相对误差值最大值0.084<0.1，意味着模型拟合效果达到较高要求。针对级比偏差值，最大值为0.069，该值小于0.1说明达到较高要求。
六、总结
灰色预测模型适用于中短期预测，所以向后1期和向后2期的数据具有价值，更多的预测数据需要特别谨慎对待。案例对1996~2007共12年的啤酒总产量数据进行灰色预测法分析，从后验差比检验发现意味着模型精度等级比较好，并且根据数据预测向后12期的数据。对模型进行残差检验时结果也表明模型达到要求，分析结束。
