格兰杰因果检验如何分析？
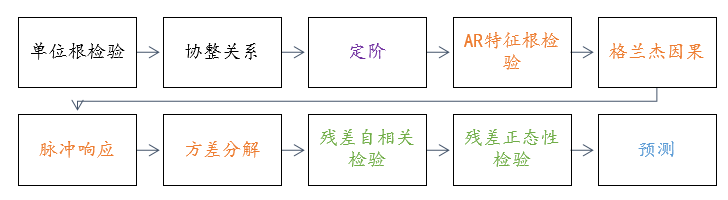
在宏观计量经济研究中，通常会使用VAR模型研究多个时间经济变量之间的数量关系情况，VAR模型时可分析各计量变量之间的影响关系及影响方差解释情况，那么该影响关系是否具有意义，此时就需要使用格兰杰检验进行研究，通常情况下格兰杰检验与VAR模型一并使用。更多关于VAR模型的构建步骤，可参考下述或SPSSAU提供的VAR模型方法帮助说明。
1 背景
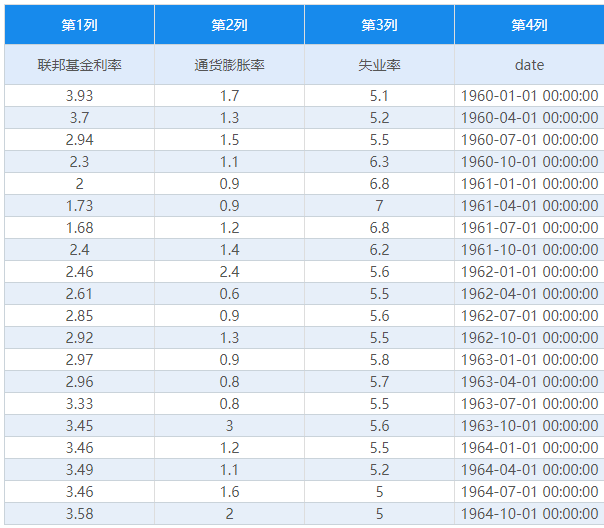
当前有一项美国宏观联邦基金利率、通货膨胀率和失业率的数据，数据日期从1960年第1季度到2012年第1季度，单位为季度，共计209个数据。现针对该3个宏观计量研究进行VAR模型构建（可参考SPSSAU中VAR模型的手册），并且使用格兰杰检验研究其‘困果关系’情况（并且VAR模型时发现1阶差分数据平稳，因此格兰杰因果检验时也使用1阶差分后数据）。部分原始数据如下图所示：
2 理论
格兰杰困果检验在原理上检验某变量是否会受到其他变量的滞后项影响，如果有这种影响关系，则称作具有granger因果关系，反之则说明没有granger因果关系。VAR模型研究计量变量之间的相关作用关系情况，因而通常需要应用格兰杰进行检验，检验各计量变量之间是否真实存在着滞后影响（因果）关系。严格的讲，格兰杰检验并不是研究困果关系，而是研究时序上的影响关系情况，但通常的认知理解即为‘因果’关系。
特别提示：
- 构建VAR模型时，如果变量均平稳无单位根，那么直接构建VAR模型即可，并不需要进行协整关系检验；当然此时也直接使用平稳数据进行格兰杰检验即可；
- 如果数据非平稳有单位根，那此进行格兰杰检验的时候，建议是以差分后的数据进行格兰杰因果检验。
3 操作
本例子数据时在前期构建VAR模型时发现1阶差分平稳，因此进行格兰杰因果检验也先对数据一阶差分，然后再进行格兰杰因果检验，1阶差分的设置在SPSSAU数据处理->生成变量中，如下图所示：
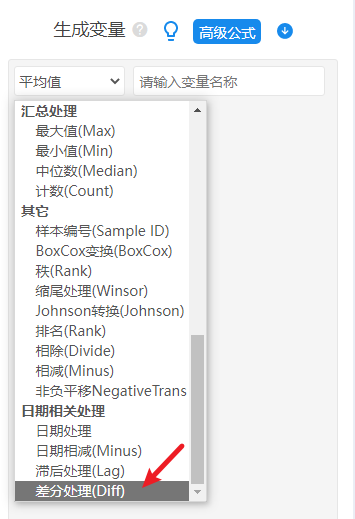
分别针对3个研究变量进行1阶差分，得到3个新标题如下：
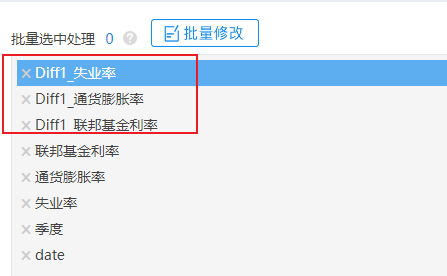
接着使用新的3个差分1阶变量进行格兰杰检验，关于格兰杰检验的操作截图如下：
关于‘滞后阶数’参数，系统默认是2阶，其意义在于：A变量影响到B变量，A变量不会马上影响到B变量，可能会隔几期才会产生影响。那么此处2阶即指A变量滞后2期会对B产生影响关系。至于此参数（滞后阶数）的设置，通常有两种做法。分别是VAR模型滞后阶数，与主观判断法，分别如下说明：
- VAR模型滞后阶数：结合VAR模型构建时设置的滞后阶数，直接同步应用到格兰杰检验中即可；
- 主观判断法：从经济意义上，多数的滞后影响均会在比如滞后1期，滞后2期就产生影响，因而通常默认设置为滞后2期等，此种设置通常需要结合自身专业知识主观综合判断。
4 SPSSAU输出结果
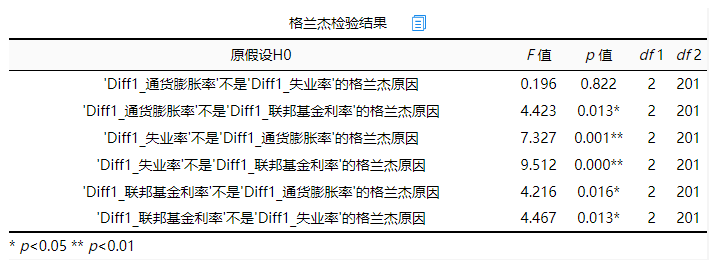
关于格兰杰granger时，SPSSAU输出一个表格，如下：
5文字分析
如果放入分析项数量为3，那么两两组合，一共就会有6个检验。本案例研究联邦基金利率、通货膨胀率和失业率这3项的格兰杰检验关系，因而共有6项。
上表格中提供F检验结果，原假设H0指并没有动态时序上的困果关系，那么如果拒绝原假设（p值<0.05）则说明具有格兰杰因果关系；反之如果接受原假设（p值>0.05），此时说明没有通过格兰杰因果检验。
从上表格可以看到：通货膨胀率与失业率之间并没有格兰杰因果关系（p值>0.05）；通货膨胀率与联邦基金利率之间有着格兰杰困果关系（p值<0.05）。与此同时，失业率分别与通货膨胀率、联邦基金利率之间也有着格兰杰因果关系；而且联邦基金利率分别与失业率、通货膨胀率之间也有着格兰杰困果关系。
除通货膨胀率与失业率之间没有呈现出显著性，另外5个检验均呈现出困果关系，那么综合来看VAR模型的构建有意义，在VAR模型时进行脉冲响应分析、方差分解分析等均有意义。如果没有呈现出困果关系，那么可考虑更换滞后阶数（通常越小越好）来进行对比分析使用等。
6 剖析
涉及以下几个关键点，分别如下：
- 关于滞后阶数这个参数的设置，通常有两种做法。分别是VAR模型滞后阶数，与主观判断法，分别如下说明：VAR模型滞后阶数：结合VAR模型构建时设置的滞后阶数，直接同步应用到格兰杰检验中即可；主观判断法：从经济意义上，多数的滞后影响均会在比如滞后1期，滞后2期就产生影响，因而通常默认设置为滞后2期等，此种设置通常需要结合自身专业知识主观综合判断。
- 格兰杰检验时，有个别没有呈现出显著性（即没有通过格兰杰检验）。理论上希望全部检验均呈现出显著性才可以，但实际研究中，会出现个别检验并没有通过格兰杰检验，但多数均通过格兰杰检验，此时建议研究者综合判断，综合认为检验结果通过可以进行VAR模型分析。但如果多数格兰杰检验均没有通过，此时建议以没有通过格兰杰检验作为结论。
7疑难解惑
- 格兰杰检验的前提条件是什么？
格兰杰检验的前提上一般要求数据平稳，因而如果VAR模型时研究变量不平稳（但同阶单整），那么此时进行格兰杰检验时，建议以差分项进行格兰杰检验，而非原始变量数据。 - 如果同阶单整时，是否可以不进行格兰杰检验？
VAR模型时，如果原始序列平稳此时不需要进行协整检验，直接进行VAR模型分析即可，并且可进行格兰杰因果检验。如果出现原始序列不平稳且满足同阶单整（且通过协整检验），此时是否进行格兰杰检验并没有固定要求，此时如果要进行格兰杰检验，通常应该以差分后的序列数据进行，而非原始不平稳序列数据。
