手把手教你用SPSSAU做K均值聚类分析
1.案例数据探索
案例采用著名的鸢尾花iris数据集,按鸢尾花的三个类别(刚毛,变色,佛吉尼亚),每一类50株,共测得150株鸢尾花的花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性数据。
1.1 浏览数据与变量
数据上传SPSSAU后,在 “我的数据”中查看浏览一下原始数据,前10行数据如下:
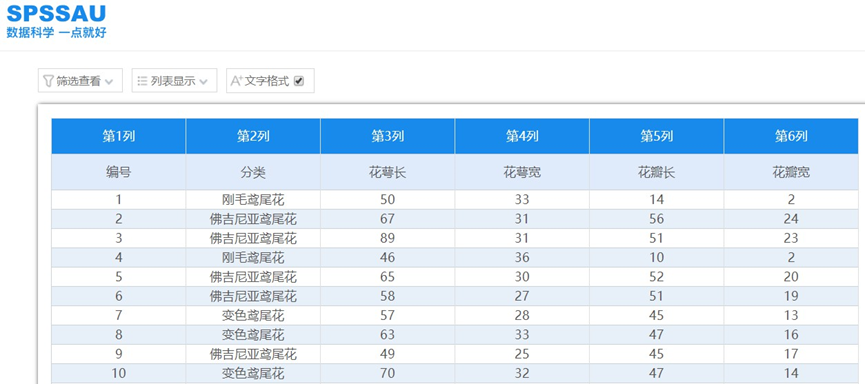
图1 “我的数据”查看浏览数据集
花瓣、花萼长宽为连续型变量,已知的鸢尾花分类数据是类别型变量。
1.2 箱线图观察数据分布
现在我们用已知的鸢尾花分类变量作为组别,来分别看一下不同类型鸢尾花群体在花瓣、花萼长宽属性上的分布情况。数据分布的探查,我们考虑用SPSSAU绘制箱线图或提琴图。
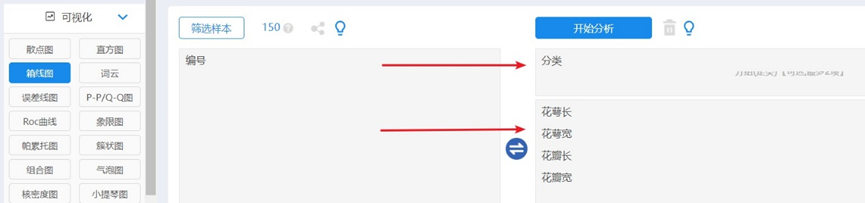
图2 箱线图绘制操作
在“可视化”栏目下选择箱线图,花瓣、花萼长宽4个变量拖拽【定量分析项】框,分类变量拖至【分组】框,点“开始分析”按钮。SPSSAU会给出每个定量指标的分组箱线图,也会给出整合后的“簇状”箱线图,4个属性的数据均在0-100内变化,所以放在同一个坐标系下仍具有可读性且信息量丰富。

图3 SPSSAU箱线图
如上图所示,刚毛鸢尾花在花瓣宽、花瓣长两个属性数据的分布上与另外两个类别差异较为明显,具体表现为刚毛鸢尾花在花瓣长、宽数据上是都是最小的,刚毛鸢尾花的花瓣面积小这个特征较明显。此外,佛吉尼亚鸢尾花似乎有更长的花萼和花瓣。
2.K均值聚类详解
2.1 分析目的与方法选择
换一个角度看待这组数据,假设这150株鸢尾花是你刚刚采集到的数据,而且你并不知道每一株花是三种中的哪一个类型,现在我们希望采取某种分类的统计学方法,来对这150株花进行分类预测。
K均值聚类是一个不错的选择,它适合样本量较大的数据集,依据连续型数据对个案进行聚类过程。在开始聚类之前,K均值算法希望我们能提供一个K值,即聚类的类的个数。对于鸢尾花数据来说,我们已知它有刚毛、变色、佛吉尼亚三个类型,因此K均值的聚类个数K值是明确的。
2.2 SPSSAU聚类操作
在“进阶方法”栏目下,选择“聚类”,花瓣、花萼长宽这4个连续型变量拖拽至【定量分析项】框内,作为K均值聚类的依据。鸢尾花已知有3个类型,因此K值=3,SPSSAU聚类个数默认即为3类,默认即可。
对于聚类过程,不同指标单位量纲有区别,因此建议做标准化处理,默认勾选【标准化】。同时,我们希望聚类结束后,能将聚类的类变量作为结果保存下来,因此默认勾选【保存类别】。
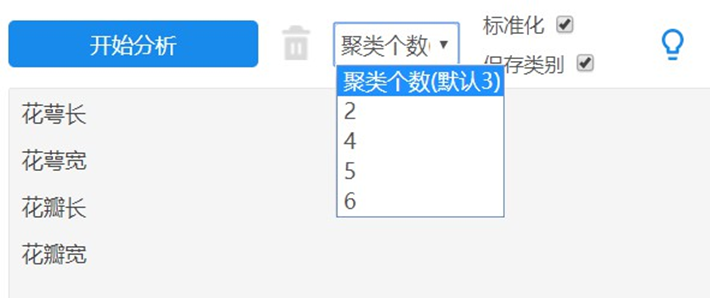
图4 聚类分析操作
如上操作,可见SPSSAU做K均值聚类整个参数选项的设定过程极为简要明了,只需要有一点统计基础即可操作。
2.3 K均值聚类通俗理解
关于K均值聚类的K值,并不一定必须已知,我们可以采取遍历的形式,譬如说在3-6类之间进行遍历,即依次选择聚为3类、4类、5类、6类,然后对聚类结果进行比较,选择最佳结果即可。就聚类分析而言,通常情况下,建议用户设置聚类数量介于2~6个之间,不宜过多。
指定K值后,算法会从数据集中随机化选择一个个案的数据作为初始聚类中心,即K个类的中心点坐标。随后计算其他个案所代表的点与初始聚类中心点的距离,并按距离远近进行分配,每完成一次分配,聚类中心都将重新计算,因此聚类中心处于变化中,这个过程不断重复,直到聚类中心点不再变化为止,此时距离数据产生的误差平方和SSE应为最小。
K均值的聚类过程,全部会有SPSSAU计算完成。我们了解基础后,直接来读取它输出的结果即可。
3.K均值聚类结果解读
3.1 类的规模
首先来看聚类后各类的规模,本例即看三类中各类群体包含的鸢尾花株数。
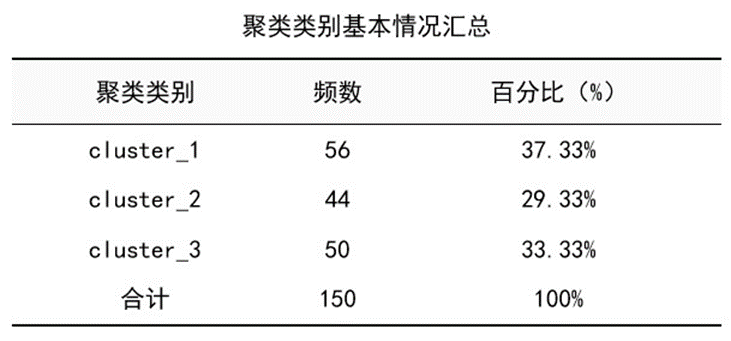
图5 类规模三线表
如上表所示,cluster1包含56株、cluster2包含44株、cluster3包含50株,个案比例依次为37.3%、29.3%和33.3%。
该数据集已知每类含同类鸢尾花50株,现在K均值聚类结果仅有cluster3含50株,其他两类的规模与50株有微小差异,初步看聚类的准确率还是不错的。
SPSSAU还为类规模表配置了一个饼图进行可视化展示,如下:
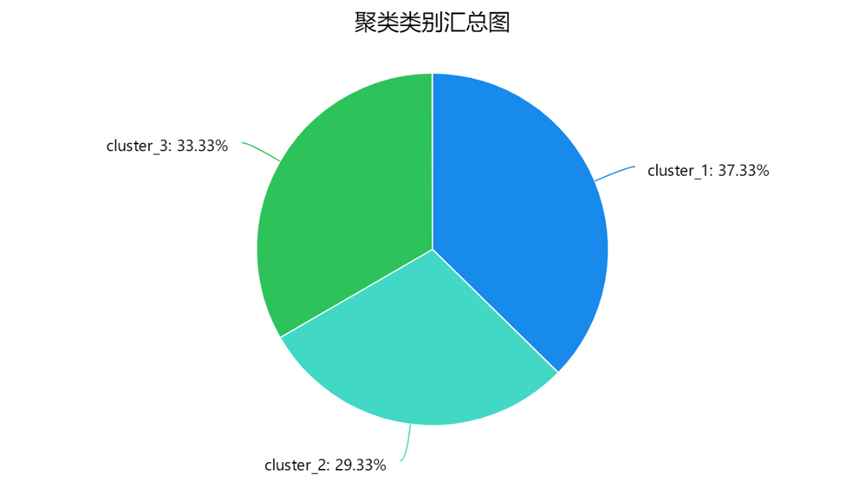
图6 SPSSAU饼图
3.2 聚类中心与SSE
前面我们通俗介绍了K均值的聚类过程,提到初始聚类中心,在迭代过程中最后会成为最终聚类中心点,这个结果SPSSAU也为大家提供了。见下表。
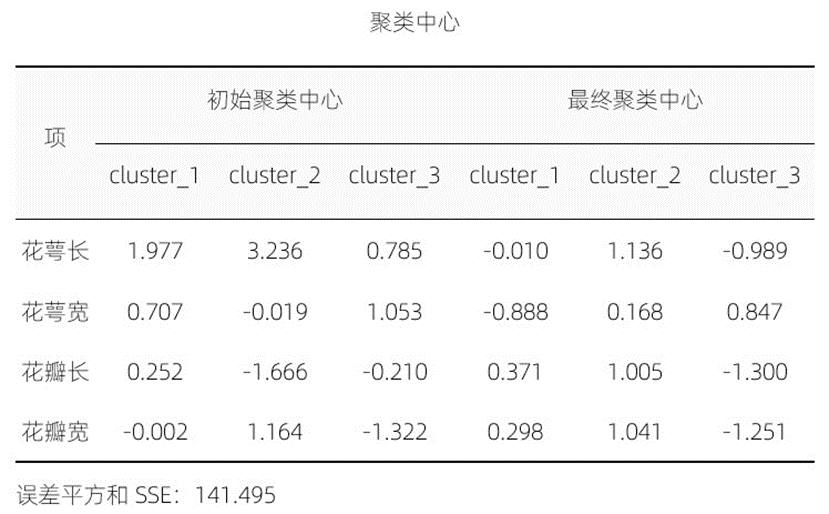
图7 初始聚类中心与最终聚类中心
表格中的属性数据是标准化后的数据,如果我们想使用最终聚类中心的话,需要转换为原始数据。对我们来说,比较重要的是该表下方备注的误差平方和SSE值,如果我们采取的是遍历聚类结果的方案,那么方案之间孰优孰劣,可以比较SSE的大小,更小的SSE表明聚类效果更佳。
3.3 类的特征与命名
现在我们思考一个问题,前面用于聚类的4个属性,即花瓣、花萼长宽数据,对于当前的K均值聚类结果来说,3个不同类之间花瓣、花萼长宽是否存在差异呢?或者说,各类在4个属性上有何特征?如果给每个类起个名字,我们的依据是什么?
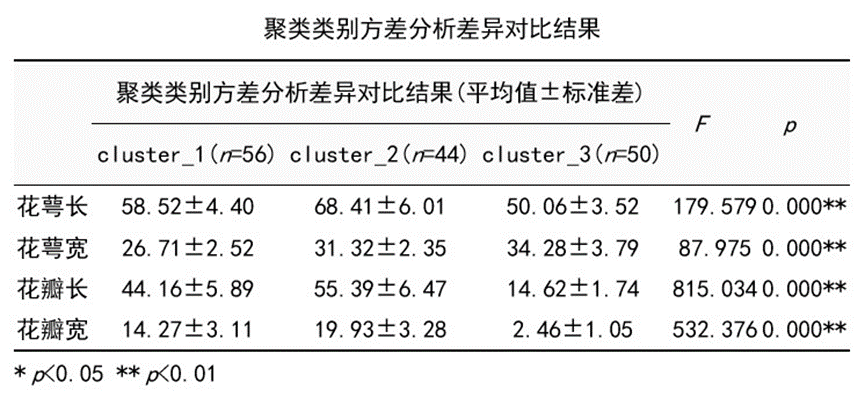
图8 聚类结果方差分析三线表
为了探索出各个类别的具体特征,因而使用方差分析去研究各个类别群体的差异性,最终可结合各个类别特征进行类别命名。
上表即方差分析表,由此可知:聚类类别群体对于所有参与聚类的指标变量均呈现出显著性(p<0.05),意味着聚类分析得到的3类群体,他们在研究项上的特征具有明显的差异性,具体差异性可通过平均值进行对比,并且最终结合实际情况,对聚类类别进行命名处理。
根据方差分析表中各类在4个属性上的均值表现,结合前面我们用箱线图对已知三种鸢尾花特征的探查,初步命名cluster3为刚毛鸢尾花类,cluster2为佛吉尼亚鸢尾花类,而cluster1为变色鸢尾花类。
SPSSAU生成的这个方差分析表格,界面是极其友好的,直接就是一个三线表外观,并且用均值±标准差的形式展示数据状况,并配方差分析F统计量、P值,而且还用*符号做标记。
该表基本符合学术要求,如果我们是写学术科研论文,那么此表稍作编辑即可放入论文中。
3.4 聚类结果的可视化展示
字不如表,表不如图,有没有可能用某种可视化图形来展示聚类结果呢?不着急,我们继续来解读SPSSAU输出的结果。
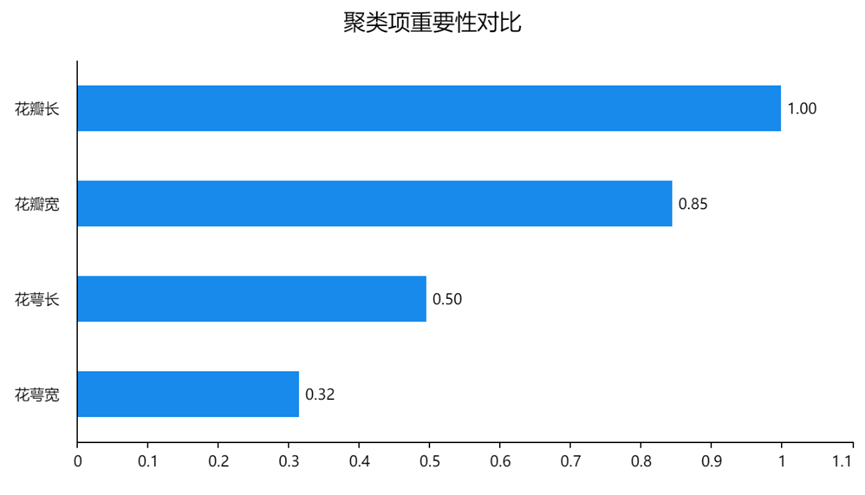
图9 聚类指标变量重要性排序
上方条形图,对参与聚类的4个属性变量,根据对聚类结果的贡献进行重要性排序。花瓣长、花瓣宽依次排名第一、第二。我们将花瓣长、花瓣宽选为最重要的两个聚类变量,接下来尝试结合SPSSAU另存出的聚类结果变量绘制散点图,以观察K均值的聚类结果。

图10 浏览查看聚类结果变量
我们再次打开数据集,此时SPSSAU已经将刚才K均值聚类的类变量保存到鸢尾花数据集中,大家看第一个变量“cluster kmeans”,它就是K均值的聚类结果。
现在,在“可视化”栏目下选择“散点图”,将刚才第一重要的花瓣长拖拽至【定量X】框内,将花瓣宽拖拽至【定量Y】框内,即将花瓣长、宽变量分别做为散点图的X轴、Y轴数据,然后将K均值的结果“cluster kmeans”变量拖拽至【颜色区分】框内,点“开始分析”命令绘制散点图。
图11 散点图操作
来看结果。
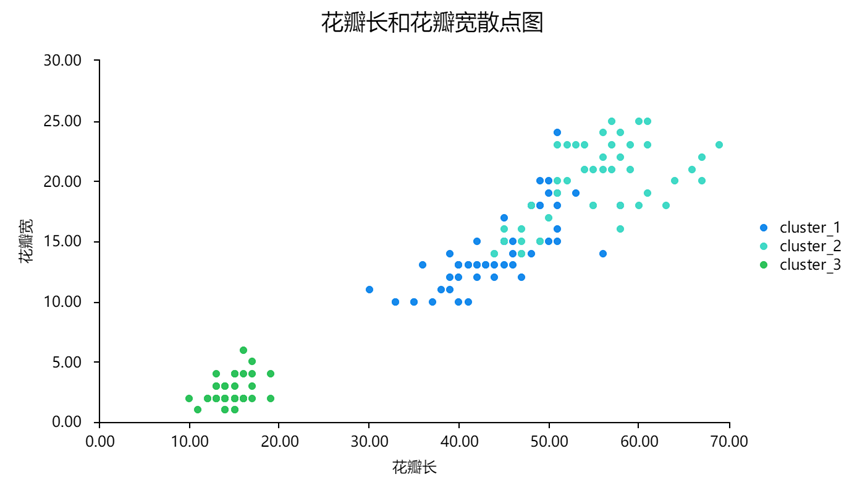
图12 SPSSAU散点图
以上操作,相当于我们以花瓣的大小来观察聚类结果。最终散点图如上图所示,花瓣最小的是cluster3即刚毛鸢尾花,花瓣相对较大的是cluster2即佛吉尼亚鸢尾花,花瓣居中的则是cluster1变色鸢尾花。
显然,刚毛鸢尾花特征最为明显(花瓣长宽最小),它的类中心和其他两个类的类中心距离足够远。而佛吉尼亚和变色鸢尾花的类中心点较近,一小部分株花无法明确划分区别,两类在花瓣特征上有微小重叠区域,佛吉尼亚鸢尾花的平均花瓣尺寸比变色鸢尾花更大一些。
总体看,基于花瓣、花萼长宽数据用K均值聚类方法可以对鸢尾花进行分类,尤其是对刚毛鸢尾花的判定准确度极高,对两外两类的分类预测存在较小的误差。
4.K均值聚类总结
K均值聚类要求参与聚类的指标变量为连续型数据,用于对样本进行分类处理。聚类个数K值,我们可以根据行业知识、经验来自行给定,也可以遍历多个聚类方案进行优选探究,一般建议聚类个数2~6个,不宜过多。
实践中,参与聚类的指标变量可能既有连续数据,也会包括分类数据。我们看到在SPSSAU的“聚类”功能下,允许同时存在连续项和分类项。此处大家应注意区分一下,如果说聚类指标变量中包括定类项,那么SPSSAU默认会进行K-prototype聚类算法(而不是kmeans算法)。
提炼信息以概括类的特征,对类进行命名,这项工作极为重要。算法给的聚类结果,如果没有独立、明确的类特征,那么其结果没有实际指导意义。
SPSSAU实现K均值聚类,操作简便,三线表直接可用,统计图形美观,结果丰富。必要时,可纳入分类变量作为聚类依据,实现K-prototype聚类算法,方法灵活,优势明显。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号