线性回归案例+分析
一、案例说明
调查不同人群对于创业方面的想法,其中认为也许影响“创业可能性”分为“科技发展”,“社会资源”和“教育水平”共3个维度,其三个维度下的分析项都是量表题,以及创业可能性也是由量表题构成,案例数据中还包括基本个体特征比如性别、年龄等,数据样本为200个。此案例主要分析目的是研究科技发展、社会资源以及教育水平对于创业可能性的影响。
二、数据处理
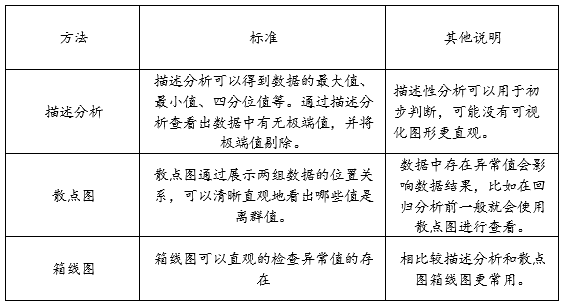
在数据分析之前,首先需要进行数据查看,案例是问卷数据所以对于数据进行查看是否有异常值,常见的方法包括利用SPSSAU描述分析看数据是否正常,散点图以及箱线图。
异常值的判断标准如下:

检验数据是否有异常值的方法:
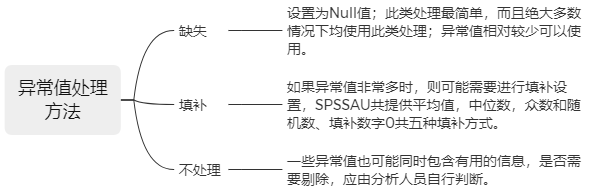
异常值处理方法:
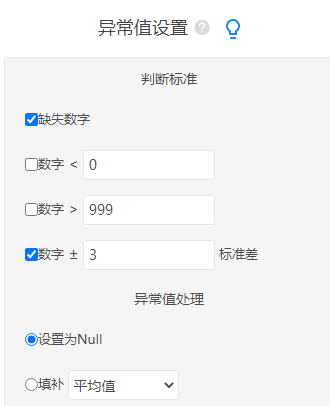
此案例对于异常值参照的标准为大于±3个标准差
使用描述分析进行查看发现没有异常值。

除了对异常值处理外,还需要对变量进行处理,由于问卷中多个量表表示一个问题所以将量表合成一个维度进行分析:
例如“我意识到科技发展对于创业的好处”、“我认为科技发展使得创业更加容易”、“我认为网络创业在中国会成为一种趋势”以及“将来我可能会以科技行业作为创业起点”,四个量表题可以表示“科技发展”利用SPSSAU数据处理中的生成变量就可以完成,如图所示:

“我认为社会关系对于创业是非常重要”、“拥有好的社会关系可以帮助创业人成就一番事业” 以及“没有好的社会关系会影响创业活动的成功”,三个量表题可以表示“社会资源”如图所示:

其它变量也是如此。处理变量后需要进行分析前的基本关系查看,比如散点图、相关性分析等,观察因变量与自变量之间是否具有线性特点、是否相关。以下一一说明。
三、基本关系查看
1.散点图
利用SPSSAU“可视化”→“散点图”做数据的散点图,观察因变量与自变量之间是否具有线性特点。

从上图中可以看出,创业可能性和教育水平、社会资源以及科技发展均存在线性关系,其中Y轴为因变量创业可能性,X轴为自变量。接下来查看数据的相关性。
2.相关性分析
相关分析是研究有没有关系,回归分析是研究影响关系。明显地,相关分析是基础,然后再进行回归分析。首先需要知道有没有相关关系;有了相关关系,才可能有回归影响关系;如果没有相关关系,是不应该有回归影响关系的。

从上表可知,利用相关分析去研究创业可能性和社会资源, 教育水平, 科技发展共3项之间的相关关系,使用Pearson相关系数去表示相关关系的强弱情况。具体分析可知:
创业可能性与教育水平共1项之间全部均呈现出显著性,相关系数值分别是0.232,全部均大于0,意味着创业可能性与教育水平共1项之间有着正相关关系。同时,创业可能性与社会资源, 科技发展共2项之间并不会呈现出显著性,相关系数值接近于0,说明创业可能性与社会资源, 科技发展共2项之间并没有相关关系。相关与回归并没有百分之百的联系,从模型完整性来讲,对于不相关的变量也可以纳入模型进行分析但是如果没有相关关系,是不应该有回归影响关系的。
四、线性回归结果
基本关系查看后,我们切入正题利用SPSSAU通用方法的线性回归进行回归分析,接下来对回归结果进行说明,其中包括模型效果以及模型结果两大部分。具体如下:
另外,模型中包括性别、年龄控制变量,控制变量指可能干扰模型的项,比如年龄,学历等基础信息。从软件角度来看,并没有“控制变量”这样的名词。“控制变量”就是自变量,所以直接放入“自变量X”框中就好。 另外,控制变量一般是定类数据,理论上控制变量需要作“虚拟(哑)变量”设置,但实际研究中很少这样做而是直接放入模型中,可能原因是“控制变量”并非核心研究项,所以不用考虑太过复杂。
1.模型效果
(1)F检验

从上表可以看出,离差平方和为162.149,残差平方和为152.062,而回归平方和为10.086。回归方程的显著性检验中,统计量F=2.574,对应的p值小于0.05,被解释变量的线性关系是显著的,可以建立模型。建立模型后,需要查看模型拟合优度是否可以,其中就可以查看R方与调整R方值。
(2)拟合优度

从上表可知,将社会资源, 教育水平, 科技发展作为自变量,而将创业可能性作为因变量进行线性回归分析,从上表可以看出,模型R方值为0.062,调整R方为0.038,其中R方是决定系数,模型拟合指标。反应Y的波动有多少比例能被X的波动描述。调整R方也是模型拟合指标。当x个数较多是调整R²比R²更为准确。意味着社会资源, 教育水平, 科技发展可以解释创业可能性的6.2%变化原因。可见,模型拟合优度一般,说明被解释变量可以被模型解释的部分较少。接下来查看变量是否具有多重共线性。
补充说明:
R平方值表示模型拟合能力的大小,比如0.3表示自变量X对于因变量Y有30%的解释能力。这个值介于0~1之间,越大越好。但实际研究中并没有固定的标准,有的专业0.1甚至0.05这样都可以,但有的专业却常常出现0.8以上。一般情况下只需要报告此值即可,不用过多关注其大小,原因在于多数时候我们更在乎X对于Y是否有影响关系即可。
(3)多重共线性
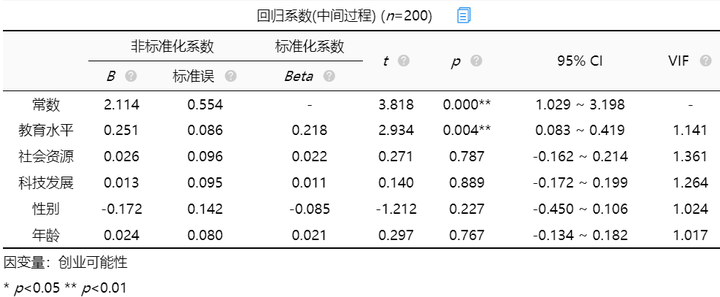
VIF值用于检测共线性问题,一般VIF值小于10即说明没有共线性(严格的标准是5),有时候会以容差值作为标准,容差值=1/VIF,所以容差值大于0.1则说明没有共线性(严格是大于0.2),VIF和容差值有逻辑对应关系,因此二选一即可,一般描述VIF值。在【线性回归】分析时,SPSSAU会智能判断共线性问题并且提供解决建议。 结果中可以看出,变量的VIF值均小于5,所以此案例不存在多重共线性的问题。
但是如果存在多重共线问题,建议三种解决方法一是使用逐步回归分析(让模型自动剔除掉共线性过高项);二是使用岭回归分析(使用数学方法解决共线性问题),三是进行相关分析,手工移出相关性非常高的分析项(通过主观分析解决),然后再做线性回归分析。
下面进行说明模型的自相关性。
(4)自相关性
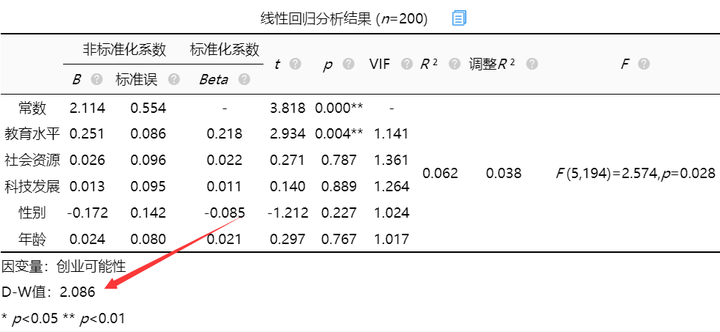
D-W值为2.086在数字2附近,因而说明模型不存在自相关性,样本数据之间并没有关联关系,模型较好(一般D-W值在时间序列模型中比较常见,一般模型不需要过度关注)。
D-W值也称Durbin-Watson值,一般对于时间序列分析才会考虑DW值:
(1)当残差与自变量互为独立时,DW≈2;
(2)当相邻两点的残差为正相关时,DW<2;
(3)当相邻两点的残差为负相关时,DW>2;
2.模型结果
回归的中间过程包括F检验、拟合优度、多重共线性以及自相关性,这些都是在分析前需要进行观测与分析的,接下来将从模型公式、分析结果、影响关系大小以及其它方面进行对模型结果的阐述。
(1)模型公式

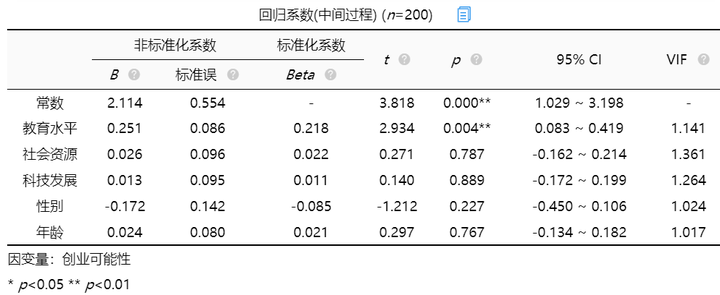
从上表可知,将教育水平,社会资源,科技发展,性别,年龄作为自变量,而将创业可能性作为因变量进行线性回归分析,从上表可以看出,模型公式为:创业可能性=2.114 + 0.251*教育水平 + 0.026*社会资源 + 0.013*科技发展-0.172*性别 + 0.024*年龄。
(2)分析结果

最终分析可知:教育水平的回归系数值为0.251(t=2.934,p=0.004<0.01),意味着教育水平会对创业可能性产生显著的正向影响关系。社会资源的回归系数值为0.026(t=0.271,p=0.787>0.05),意味着社会资源并不会对创业可能性产生影响关系。科技发展的回归系数值为0.013(t=0.140,p=0.889>0.05),意味着科技发展并不会对创业可能性产生影响关系。
性别的回归系数值为-0.172(t=-1.212,p=0.227>0.05),意味着性别并不会对创业可能性产生影响关系。年龄的回归系数值为0.024(t=0.297,p=0.767>0.05),意味着年龄并不会对创业可能性产生影响关系。
总结分析可知:教育水平会对创业可能性产生显著的正向影响关系。但是社会资源, 科技发展, 性别, 年龄并不会对创业可能性产生影响关系。
(3)影响关系大小
如果说自变量X已经对因变量Y产生显著影响(P< 0.05),还想对比影响大小,建议可使用标准化系数值的大小对比影响大小,Beta值大于0时正向影响,该值越大说明影响越大。Beta值小于0时负向影响,该值越小说明影响越大。上图所示,回归方程的常数项约为2.114,教育水平,社会资源,科技发展,性别,年龄的标准化系数分别为0.218、0.022、0.011、-0.085、0.021。可以看出模型中教育水平对创业可能性影响较大。
(4)其它
除此之外,SPSSAU还提供了线性回归分析结果-简化格式以及coefPlot。
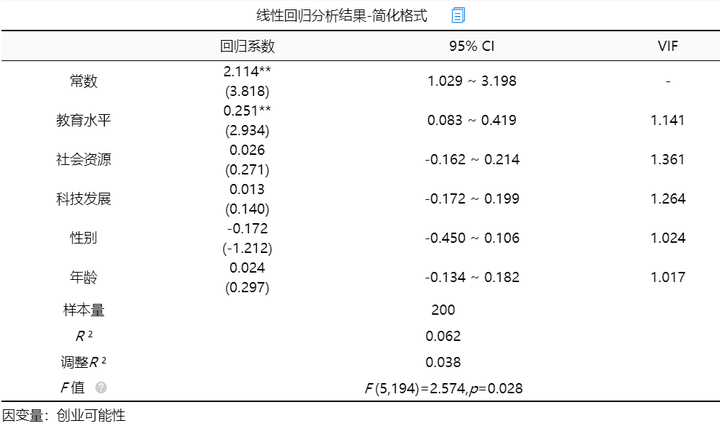

coefPlot展示具体的回归系数值和对应的置信区间,可直观查看数据的显著性情况,如果说置信区间包括数字0则说明该项不显著,如果置信区间不包括数字0则说明该项呈现出显著性。所以上图中只有教育水平不包括0,呈现显著性。接下来对分析后的模型进行稳健性检验。
五、稳健性检验
稳健性检验是指模型的稳定性,使用多种形式时模型均稳定,应该显著的项还是显著,不显著的依旧不显著。一般情况下建议在线性回归时考虑加入控制变量,和不加入控制变量两种情况下对比模型的稳定性,当然也可以使用多种研究方法比如线性回归,逐步回归,分层回归等,多种方法测试同一个变量的显著性情况是否有着变化,如果无论如何均稳定或者极个别在变化,均说明模型具有稳健性。方法说明如下:
本次分析选择第一个分析方法,对于放置控制变量与不放置控制变量进行分析对比:
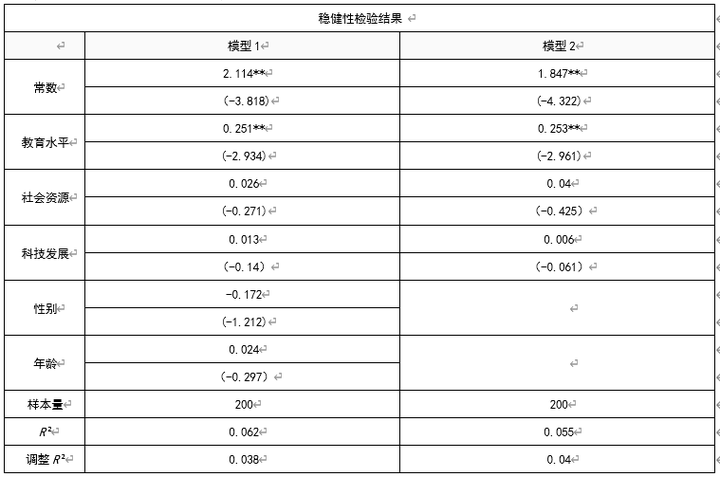
教育水平会对创业可能性产生显著的正向影响关系。但是社会资源, 科技发展并不会对创业可能性产生影响关系。总结可知,前后对比发现自变量显著性未发生改变模型具有稳健性。
六、总结
研究科技发展、社会资源以及教育水平对于创业可能性的影响。首先对数据进行处理其中包括异常值以及量表题合成一个维度,接下来对于基本关系进行查看,包括线性关系以及相关关系,在分析时模型加入了控制变量,从两个大方面进行分析包括模型效果以及模型结果,发现教育水平会对创业可能性产生显著的正向影响关系。但是社会资源, 科技发展, 性别, 年龄并不会对创业可能性产生影响关系。进行稳健性检验使用是否加入控制变量的方法,发现模型具有稳健性。分析结束。
更多干货请登录SPSSAU官方网站查看。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号