主成分有什么用？如何进行呢？
一、研究背景
主成分分析用于对数据信息进行浓缩，比如总共有20个指标值，是否可以将此20项浓缩成4个概括性指标。除此之外，主成分分析可用于权重计算和综合竞争力研究。即主成分分共有三个实际应用场景：
二、数据格式
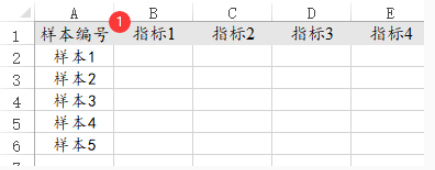
主成分分析时，一列标识1个指标，一行为1个样本；如果为面板数据，比如100家公司每家公司10年，那么就会有100*10=1000个样本，可能需要单独两列分别是公司名和年份来标识面板格式而已，但主成分分析并不区分是否面板数据，只针对指标进行分析即可，另一般分析样本量需要超出分析项（指标）的5倍，类似数据格式如下图：
三、SPSSAU操作
1.上传数据
登录账号后进入SPSSAU页面，点击右上角“上传数据”，将处理好的数据进行“点击上传文件”上传即可。
2.拖拽分析项
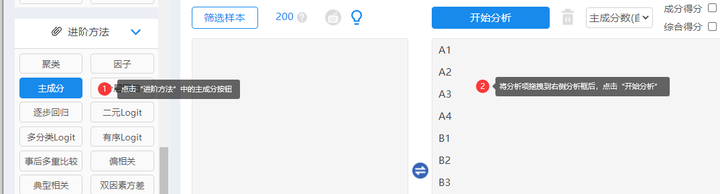
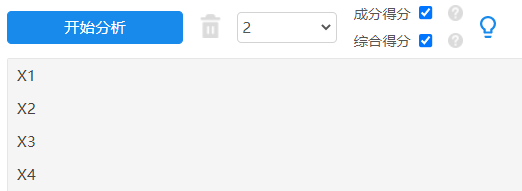
可以勾选“成分得分”以及“综合得分”点击开始分析后，左侧分析框就会出现，成分得分与综合得分：
四、SPSSAU分析
背景：当前有一份数据,共涉及9个指标，希望将此9个指标使用主成分分析进行降维，并计算综合得分。
1.KMO 和 Bartlett 的检验
使用主成分分析进行信息浓缩研究，首先分析研究数据是否适合进行主成分分析，从上表可以看出：KMO为0.913，大于0.6，满足主成分分析的前提要求，意味着数据可用于主成分分析研究。以及数据通过Bartlett 球形度检验(p<0.05)，说明研究数据适合进行主成分分析。
2.方差解释率表格
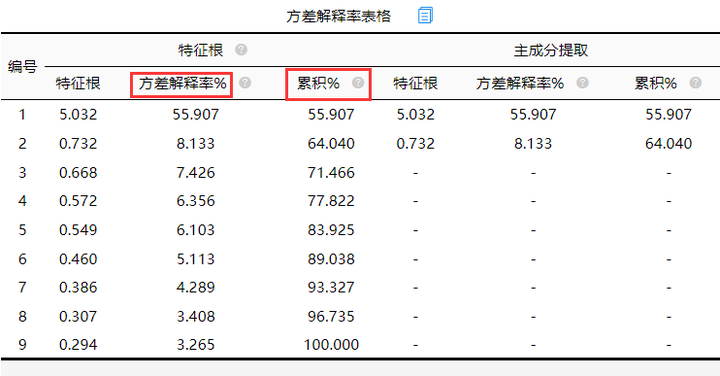
上表格针对主成分提取情况，以及主成分提取信息量情况进行分析，从上表可知：主成分分析一共提取出2个主成分，此2个主成分方差解释率分别是55.907%,8.133%，累积方差解释率为64.040%另外，本次分析共提取出2个主成分，它们对应的加权后方差解释率即权重依次为：55.907/64.040=87.30%；8.133/64.040=12.70%；
3.载荷系数表格
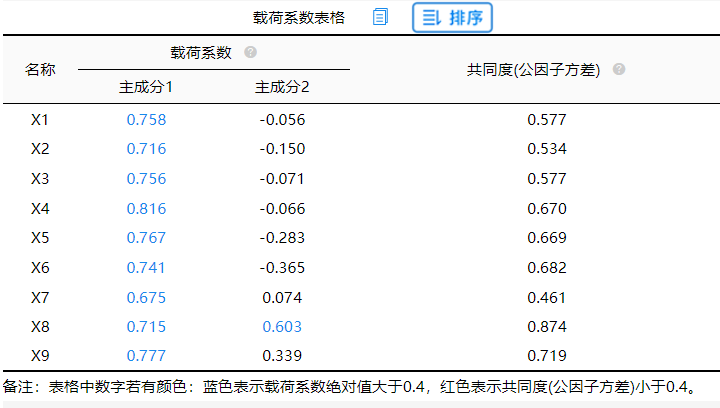
载荷系数表格，主要展示主成分对于研究项的信息提取情况，以及主成分和研究项对应关系。
共同度代表某题项可被提取的信息量，共同度越高说明指标能被主成分解释的程度越高，被提取的信息量越多。一般以0.4作为标准。
上表格展示主成分对于研究项的信息提取情况，以及主成分和研究项对应关系，从上表可知：所有研究项对应的共同度值均高于0.4，意味着研究项和主成分之间有着较强的关联性，主成分可以有效的提取出信息。确保主成分可以提取出研究项大部分的信息量之后，接着分析主成分和研究项的对应关系情况（载荷系数绝对值大于0.4时即说明该项和主成分有对应关系）。
补充说明：如果主成分分析结果不佳，可考虑使用因子分析，在主成分分析的基础上，因子分析多出旋转功能，更容易找出因子和分析项对应关系。
4.成份得分系数矩阵
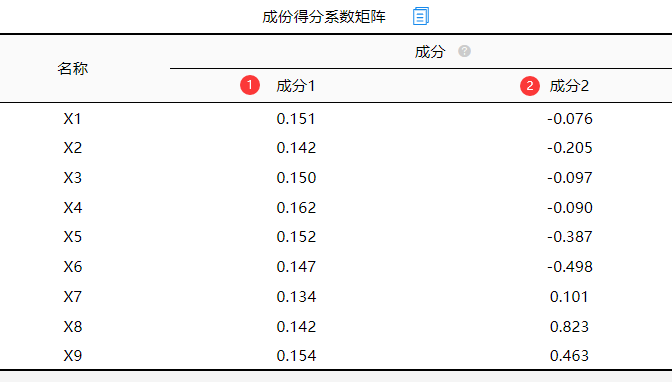
使用主成分分析目的在于信息浓缩，则忽略“成份得分系数矩阵”表格。如果使用主成分分析法进行权重计算，则需要使用“成份得分系数矩阵”建立主成分和研究项之间的关系等式（基于标准化后数据建立关系表达式），如下：
（1）成分得分1（成分1）=
0.151*X1+0.142*X2+0.150*X3+0.162*X4+0.152*X5+0.147*X6+0.134*X7+0.142*X8+0.154*X9；
（2）成分得分2（成分2）=
-0.076*X1-0.205*X2-0.097*X3-0.090*X4-0.387*X5-0.498*X6+0.101*X7+0.823*X8+0.463*X9；
5.碎石图
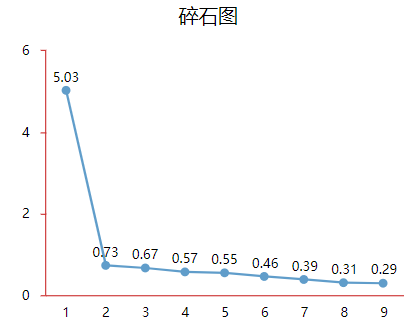
可结合碎石图辅助判断主成分提取个数。当折线由陡峭突然变得平稳时，陡峭到平稳对应的主成分个数即为参考提取主成分个数。实际研究中更多以专业知识，结合主成分与研究项对应关系情况，综合权衡判断得出主成分个数。图中可以看出当横坐标为2时，折线突然变得比较平稳。
6.载荷图
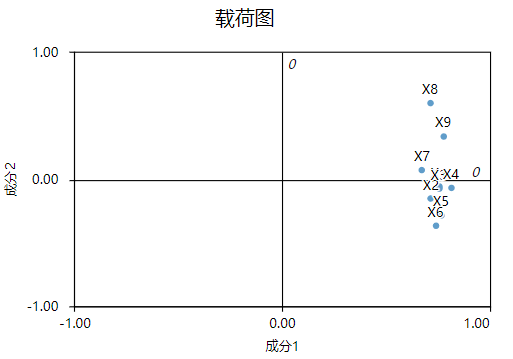
载荷图是针对成分与旋转后载荷值关系的图形化展示，使用较少，通常需要手工加‘圆圈’把挨在一起的因子圈起来，更直观展示成分与分析项的隶属对应关系情况。由于可读性和解释性问题，一般只关注于方差解释率靠前的前面几个成分，多数情况下只关注2个。
7.线性组合系数及权重结果
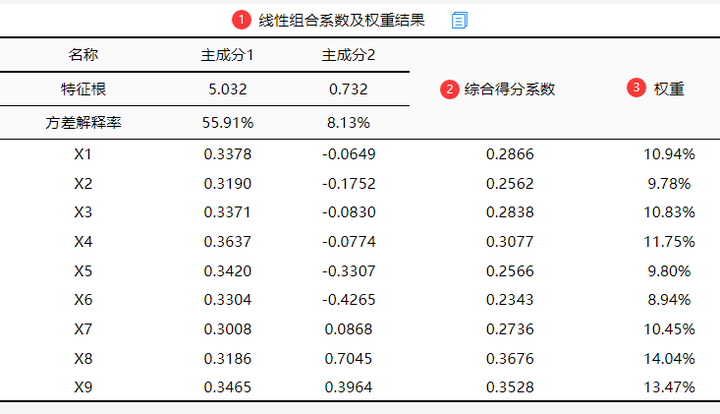
SPSSAU的主成分分析结果中默认提供“线性组合系数及权重结果表”包括上述的过程值及结果，包括线性组合系数、综合得分系数、以及指标各自的权重。
6.综合得分排名
根据之前勾选的“综合得分”，即可自动得到综合得分结果。
SPSSAU默认命名为CompScore_XXXX。使用【数据处理】→【标题处理】功能可以对题目重命名。
【数据处理】→【生成变量】里的排名功能。点击“综合得分”，再选择“排名（Rank）”，点击确认处理。
右上角“我的数据”也可以将数据进行下载。
五、其它说明
1. 提示出现奇异矩阵？
如果提示出现“奇异矩阵”，通常情况下由于分析样本量太少（比如分析项有20个，分析样本仅10个），此里需要加大样本量或者减少分析项即可；以及还有一种情况是分析项之间的相关性非常非常弱或者非常非常强，此时需要移除掉相关性非常弱或者非常强的分析项（使用相关分析进行检查相关关系）。
2. ‘分析之前是否需要对数据进行标准化处理’？
SPSSAU默认就已经进行过标准化处理，因此不需要再对数据处理。当然标准化后的数据再次标准化依旧还是自身没有任何变化，结果永远均一致。
3.综合得分如何使用？
SPSSAU默认可保存综合得分（以及因子得分等）；一般该值越大表示越有竞争力等；研究者通常需要把综合得分的具体数据下载后使用，并且在EXCEL进行排序（也可使用SPSSAU生成变量里面的排序功能）。 通过右上角我的数据可下载具体综合得分的具体数据等。
4.特征根值没有大于1可以吗？
主成分分析时通常需要综合自己的专业知识，以及软件结果进行综合判断，即使是特征根值小于1，也一样可以提取主成分。
5.主成分回归是什么意思？
进行主成分时，选择保存‘成分得分’，然后利用系统生成的‘成分得分’数据进行线性回归，即为主成分回归。
6.累积方差解释率出现100%以上如何办？
正常情况下，累积方差解释率会小于100%，但如果数据的共线性问题太严重，有可能出现方差解释率值大于100%，此时建议进行相关分析，找出相关性太强（比如相关系数大于0.8）的项，然后从分析框中移出后再次分析。与此同时，如果样本量太少也可能出现此问题建议加大样本量即可。
7. KMO值过低？
一般需要KMO值大于0.6即可，如果是两个分析项，KMO值一定是0.5；因而建议删除掉共同度(公因子方差)值较低项，这样可以提升KMO值。
如果不输出KMO值，意味着数据质量过差，建议可使用相关分析看下相关关系，如果相关系数值基本均小于0.3（或者没有呈现出显著性），则说明题项间关联性弱，则KMO值一定会较低，建议先移除相关系数值较低项后再次分析。
提示：KMO值综合衡量分析项间的信息重叠情况（即分析项之间的相关关系情况）。分析项之间的相关系数过低（比如小于0.2或没有显著性），信息重叠度低无法有效浓缩信息，这会导致KMO值较低，如果分析项之间的相关系数过高（比如大于0.8），这会导致严重共线性可能无法输出KMO值。分析项之间的相关系数值一般希望介于0.3~0.7之间较好。
六、总结
主成分分析的原理在于信息浓缩，对于信息浓缩的帮助越大，指标权重可越大，正是利用此原理，可进行指标权重的计算。主成分分析的作用更多侧重于计算权重、计算综合竞争力。不会过多关注主成分与分析项对应关系，不要求每个主成分有明确的含义。
更多干货请前往SPSSAU官网查看
