Sparse Autoencoder(二)
Gradient checking and advanced optimization
In this section, we describe a method for numerically checking the derivatives computed by your code to make sure that your implementation is correct. Carrying out the derivative checking procedure described here will significantly increase your confidence in the correctness of your code.
Suppose we want to minimize
as a function of
. For this example, suppose
, so that
. In this 1-dimensional case, one iteration of gradient descent is given by
Suppose also that we have implemented some function
that purportedly computes
, so that we implement gradient descent using the update
.
Recall the mathematical definition of the derivative as
Thus, at any specific value of
, we can numerically approximate the derivative as follows:
Thus, given a function
that is supposedly computing
, we can now numerically verify its correctness by checking that
The degree to which these two values should approximate each other will depend on the details of
. But assuming
, you'll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).
Suppose we have a function
that purportedly computes
; we'd like to check if
is outputting correct derivative values. Let
, where
is the
-th basis vector (a vector of the same dimension as
, with a "1" in the
-th position and "0"s everywhere else). So,
is the same as
, except its
-th element has been incremented by EPSILON. Similarly, let
be the corresponding vector with the
-th element decreased by EPSILON. We can now numerically verify
's correctness by checking, for each
, that:
参数为向量,为了验证每一维的计算正确性,可以控制其他变量
When implementing backpropagation to train a neural network, in a correct implementation we will have that
This result shows that the final block of psuedo-code in Backpropagation Algorithm is indeed implementing gradient descent. To make sure your implementation of gradient descent is correct, it is usually very helpful to use the method described above to numerically compute the derivatives of
, and thereby verify that your computations of
and
are indeed giving the derivatives you want.
Autoencoders and Sparsity
Anautoencoder neural network is an unsupervised learning algorithm that applies backpropagation, setting the target values to be equal to the inputs. I.e., it uses
.
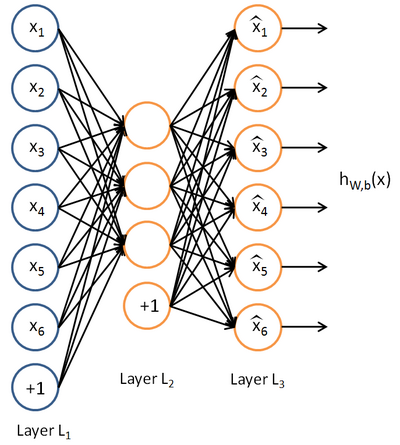
Here is an autoencoder:
we will write
to denote the activation of this hidden unit when the network is given a specific input
. Further, let
be the average activation of hidden unit
(averaged over the training set). We would like to (approximately) enforce the constraint
where
is a sparsity parameter, typically a small value close to zero (say
). In other words, we would like the average activation of each hidden neuron
to be close to 0.05 (say). To satisfy this constraint, the hidden unit's activations must mostly be near 0.
To achieve this, we will add an extra penalty term to our optimization objective that penalizes
deviating significantly from
. Many choices of the penalty term will give reasonable results. We will choose the following:
Here,
is the number of neurons in the hidden layer, and the index
is summing over the hidden units in our network. If you are familiar with the concept of KL divergence, this penalty term is based on it, and can also be written
Our overall cost function is now
where
is as defined previously, and
controls the weight of the sparsity penalty term. The term
(implicitly) depends on
also, because it is the average activation of hidden unit
, and the activation of a hidden unit depends on the parameters
.
Visualizing a Trained Autoencoder
Consider the case of training an autoencoder on
images, so that
. Each hidden unit
computes a function of the input:
We will visualize the function computed by hidden unit
---which depends on the parameters
(ignoring the bias term for now)---using a 2D image. In particular, we think of
as some non-linear feature of the input
If we suppose that the input is norm constrained by
, then one can show (try doing this yourself) that the input which maximally activates hidden unit
is given by setting pixel
(for all 100 pixels,
) to
By displaying the image formed by these pixel intensity values, we can begin to understand what feature hidden unit
is looking for.
对一幅图像进行Autoencoder ,前面的隐藏结点一般捕获的是边缘等初级特征,越靠后隐藏结点捕获的特征语义更深。

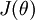 as a function of
as a function of 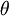 . For this example, suppose
. For this example, suppose 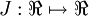 , so that
, so that 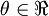 . In this 1-dimensional case, one iteration of gradient descent is given by
. In this 1-dimensional case, one iteration of gradient descent is given by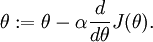
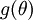 that purportedly computes
that purportedly computes 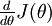 , so that we implement gradient descent using the update
, so that we implement gradient descent using the update 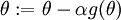 .
.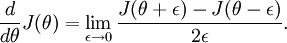
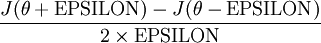
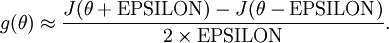
 . But assuming
. But assuming 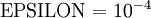 , you'll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).
, you'll usually find that the left- and right-hand sides of the above will agree to at least 4 significant digits (and often many more).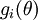 that purportedly computes
that purportedly computes 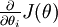 ; we'd like to check if
; we'd like to check if 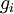 is outputting correct derivative values. Let
is outputting correct derivative values. Let 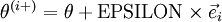 , where
, where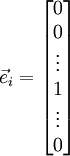
 -th basis vector (a vector of the same dimension as
-th basis vector (a vector of the same dimension as  is the same as
is the same as 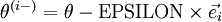 be the corresponding vector with the
be the corresponding vector with the 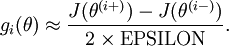
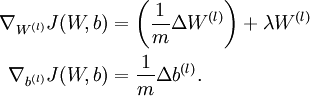
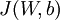 , and thereby verify that your computations of
, and thereby verify that your computations of 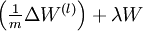 and
and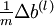 are indeed giving the derivatives you want.
are indeed giving the derivatives you want.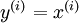 .
.
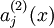 to denote the activation of this hidden unit when the network is given a specific input
to denote the activation of this hidden unit when the network is given a specific input  . Further, let
. Further, let![\begin{align}
\hat\rho_j = \frac{1}{m} \sum_{i=1}^m \left[ a^{(2)}_j(x^{(i)}) \right]
\end{align}](http://deeplearning.stanford.edu/wiki/images/math/8/7/2/8728009d101b17918c7ef40a6b1d34bb.png)
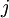 (averaged over the training set). We would like to (approximately) enforce the constraint
(averaged over the training set). We would like to (approximately) enforce the constraint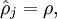
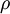 is a sparsity parameter, typically a small value close to zero (say
is a sparsity parameter, typically a small value close to zero (say 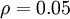 ). In other words, we would like the average activation of each hidden neuron
). In other words, we would like the average activation of each hidden neuron 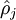 deviating significantly from
deviating significantly from 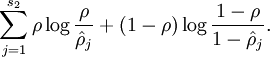
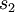 is the number of neurons in the hidden layer, and the index
is the number of neurons in the hidden layer, and the index 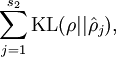
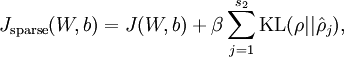
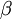 controls the weight of the sparsity penalty term. The term
controls the weight of the sparsity penalty term. The term 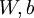 also, because it is the average activation of hidden unit
also, because it is the average activation of hidden unit 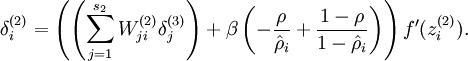
 images, so that
images, so that 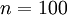 . Each hidden unit
. Each hidden unit 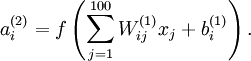
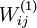 (ignoring the bias term for now)---using a 2D image. In particular, we think of
(ignoring the bias term for now)---using a 2D image. In particular, we think of 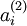 as some non-linear feature of the input
as some non-linear feature of the input 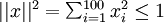 , then one can show (try doing this yourself) that the input which maximally activates hidden unit
, then one can show (try doing this yourself) that the input which maximally activates hidden unit 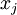 (for all 100 pixels,
(for all 100 pixels, 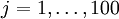 ) to
) to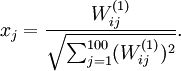

 浙公网安备 33010602011771号
浙公网安备 33010602011771号