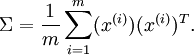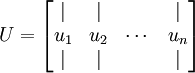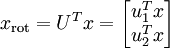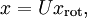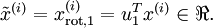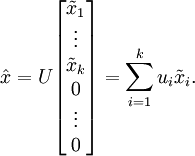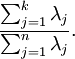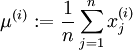PCA

http://deeplearning.stanford.edu/wiki/index.php/PCA

Principal Components Analysis (PCA) is a dimensionality reduction algorithm that can be used to significantly speed up your unsupervised feature learning algorithm.

example

Suppose you are training your algorithm on images. Then the input will be somewhat redundant, because the values of adjacent pixels in an image are highly correlated. Concretely, suppose we are training on 16x16 grayscale image patches. Then \textstyle x \in \Re^{256} are 256 dimensional vectors, with one feature \textstyle x_j corresponding to the intensity of each pixel. Because of the correlation between adjacent pixels, PCA will allow us to approximate the input with a much lower dimensional one, while incurring very little error.

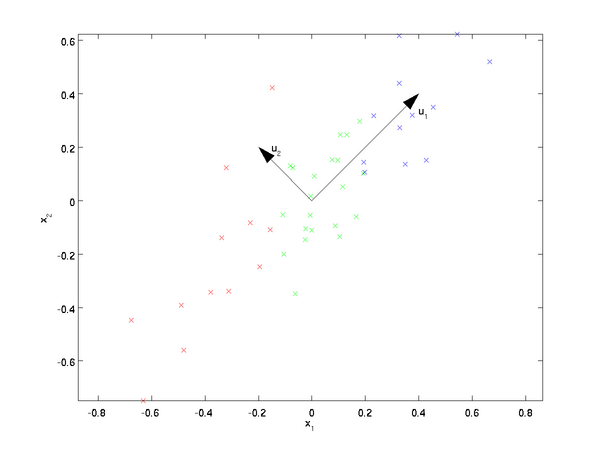
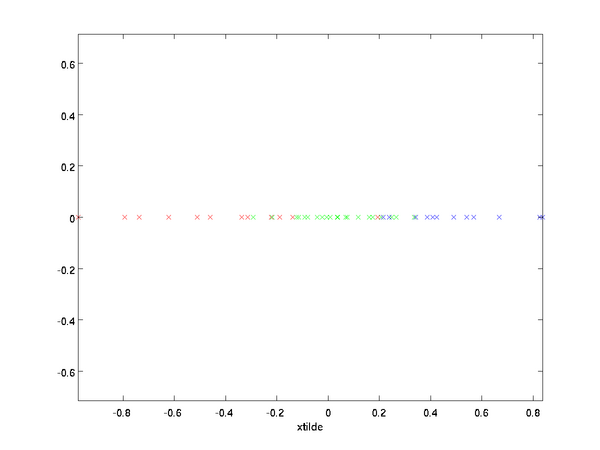
PCA will find a lower-dimensional subspace onto which to project our data. From visually examining the data, it appears that\textstyle u_1 is the principal direction of variation of the data, and \textstyle u_2 the secondary direction of variation:

PCA-u1.png

the data varies much more in the direction \textstyle u_1 than \textstyle u_2.

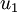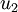To more formally find the directions \textstyle u_1 and \textstyle u_2, we first compute the matrix 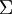\textstyle \Sigma as follows:

\begin{align} \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}

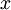If \textstyle x has zero mean, then 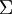\textstyle \Sigma is exactly the covariance matrix of 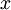\textstyle x. (The symbol "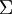\textstyle \Sigma", pronounced "Sigma", is the standard notation for denoting the covariance matrix. Unfortunately it looks just like the summation symbol, as in 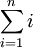\sum_{i=1}^n i; but these are two different things.)

let us compute the eigenvectors of 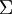\textstyle \Sigma, and stack the eigenvectors in columns to form the matrix \textstyle U:

\begin{align} U = \begin{bmatrix} | & | & & | \\ u_1 & u_2 & \cdots & u_n \\ | & | & & | \end{bmatrix} \end{align}

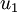Here, \textstyle u_1 is the principal eigenvector (corresponding to the largest eigenvalue), 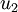\textstyle u_2 is the second eigenvector, and so on. Also, let 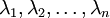\textstyle \lambda_1, \lambda_2, \ldots, \lambda_n be the corresponding eigenvalues.

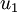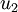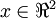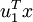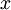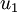The vectors \textstyle u_1 and \textstyle u_2 in our example form a new basis in which we can represent the data. Concretely, let \textstyle x \in \Re^2 be some training example. Then \textstyle u_1^Tx is the length (magnitude) of the projection of \textstyle x onto the vector \textstyle u_1.

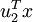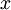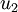Similarly, \textstyle u_2^Tx is the magnitude of \textstyle x projected onto the vector \textstyle u_2.

 

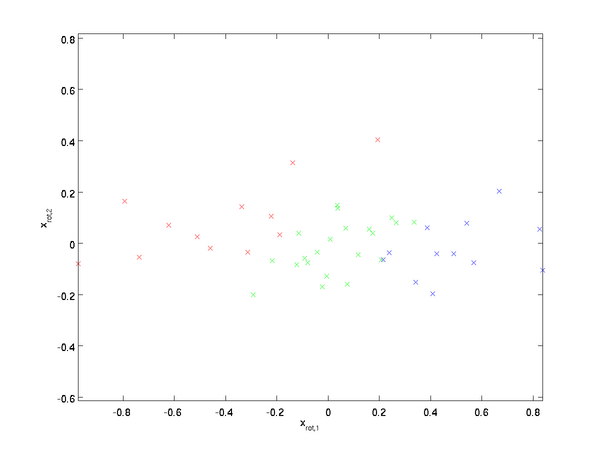
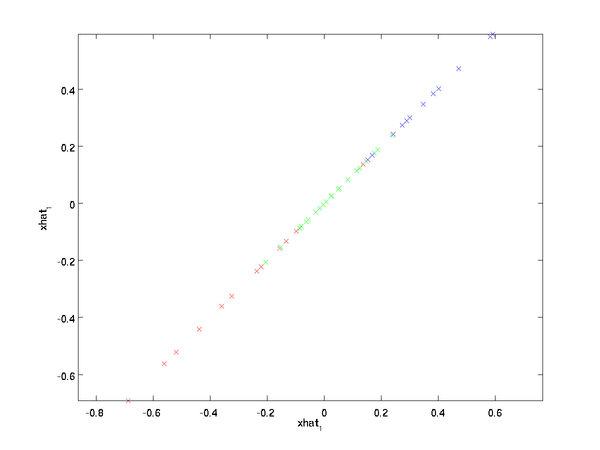
Rotating the Data

 

 

 

 

 

Thus, we can represent \textstyle x in the \textstyle (u_1, u_2)-basis by computing

\begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}

(The subscript "rot" comes from the observation that this corresponds to a rotation (and possibly reflection) of the original data.) Lets take the entire training set, and compute \textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)} for every \textstyle i. Plotting this transformed data \textstyle x_{\rm rot}, we get:

PCA-rotated.png

This is the training set rotated into the \textstyle u_1,\textstyle u_2 basis. In the general case, \textstyle U^Tx will be the training set rotated into the basis \textstyle u_1,\textstyle u_2, ...,\textstyle u_n.

One of the properties of \textstyle U is that it is an "orthogonal" matrix, which means that it satisfies \textstyle U^TU = UU^T = I. So if you ever need to go from the rotated vectors \textstyle x_{\rm rot} back to the original data \textstyle x, you can compute

\begin{align} x = U x_{\rm rot} , \end{align}

because \textstyle U x_{\rm rot} = UU^T x = x.

 

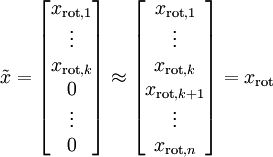
Reducing the Data Dimension

We see that the principal direction of variation of the data is the first dimension \textstyle x_{{\rm rot},1} of this rotated data. Thus, if we want to reduce this data to one dimension, we can set

\begin{align} \tilde{x}^{(i)} = x_{{\rm rot},1}^{(i)} = u_1^Tx^{(i)} \in \Re. \end{align}

More generally, if \textstyle x \in \Re^n and we want to reduce it to a \textstyle k dimensional representation \textstyle \tilde{x} \in \Re^k (where \textstyle k < n), we would take the first \textstyle k components of \textstyle x_{\rm rot}, which correspond to the top \textstyle k directions of variation.

\begin{align} \tilde{x} = \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{{\rm rot},1} \\ \vdots \\ x_{{\rm rot},k} \\ x_{{\rm rot},k+1} \\ \vdots \\ x_{{\rm rot},n} \end{bmatrix} = x_{\rm rot} \end{align}

In our example, this gives us the following plot of \textstyle \tilde{x} (using \textstyle n=2, k=1):

PCA-xtilde.png

However, since the final \textstyle n-k components of \textstyle \tilde{x} as defined above would always be zero, there is no need to keep these zeros around, and so we define \textstyle \tilde{x} as a \textstyle k-dimensional vector with just the first \textstyle k (non-zero) components.

This also explains why we wanted to express our data in the \textstyle u_1, u_2, \ldots, u_n basis: Deciding which components to keep becomes just keeping the top \textstyle k components. When we do this, we also say that we are "retaining the top \textstyle k PCA (or principal) components."

 

Recovering an Approximation of the Data

 

we can think of \textstyle \tilde{x} as an approximation to \textstyle x_{\rm rot}, where we have set the last \textstyle n-k components to zeros. Thus, given \textstyle \tilde{x} \in \Re^k, we can pad it out with \textstyle n-k zeros to get our approximation to \textstyle x_{\rm rot} \in \Re^n. Finally, we pre-multiply by \textstyle U to get our approximation to \textstyle x. Concretely, we get

\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}

 


PCA-xhat.png

We are thus using a 1 dimensional approximation to the original dataset.

 

Number of components to retain

 

To decide how to set \textstyle k, we will usually look at the percentage of variance retained for different values of \textstyle k. Concretely, if \textstyle k=n, then we have an exact approximation to the data, and we say that 100% of the variance is retained. I.e., all of the variation of the original data is retained. Conversely, if \textstyle k=0, then we are approximating all the data with the zero vector, and thus 0% of the variance is retained.

More generally, let \textstyle \lambda_1, \lambda_2, \ldots, \lambda_n be the eigenvalues of \textstyle \Sigma (sorted in decreasing order), so that \textstyle \lambda_j is the eigenvalue corresponding to the eigenvector \textstyle u_j. Then if we retain \textstyle k principal components, the percentage of variance retained is given by:

\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}. \end{align}

In our simple 2D example above, \textstyle \lambda_1 = 7.29, and \textstyle \lambda_2 = 0.69. Thus, by keeping only \textstyle k=1 principal components, we retained \textstyle 7.29/(7.29+0.69) = 0.913, or 91.3% of the variance.

 

PCA on Images

 

For PCA to work, usually we want each of the features \textstyle x_1, x_2, \ldots, x_n to have a similar range of values to the others (and to have a mean close to zero). If you've used PCA on other applications before, you may therefore have separately pre-processed each feature to have zero mean and unit variance, by separately estimating the mean and variance of each feature \textstyle x_j. However, this isn't the pre-processing that we will apply to most types of images. Specifically, suppose we are training our algorithm on natural images, so that \textstyle x_j is the value of pixel \textstyle j. By "natural images," we informally mean the type of image that a typical animal or person might see over their lifetime.

In detail, in order for PCA to work well, informally we require that (i) The features have approximately zero mean, and (ii) The different features have similar variances to each other. With natural images, (ii) is already satisfied even without variance normalization, and so we won't perform any variance normalization.

Concretely, if \textstyle x^{(i)} \in \Re^{n} are the (grayscale) intensity values of a 16x16 image patch (\textstyle n=256), we might normalize the intensity of each image \textstyle x^{(i)} as follows:

\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_j

x^{(i)}_j := x^{(i)}_j - \mu^{(i)}, for all \textstyle j

posted @ 2014-09-14 16:12  老姨  阅读(222)  评论(0)  编辑  收藏  举报