DS博客作业--查找

0.PTA得分截图

1.本周学习总结

查找

查找定义

查找：给定的某个值，在查找表中确定一个其关键字等于给定值的数据
关键字：数据元素中某个数据项的值

平均查找长度（ASL）：需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。
ASL = ΣPi×Ci （i=1，2，....，n）
Pi：查找表中第i个数据元素的概率。
Ci：找到第i个数据元素时已经比较过的次数。

查找分类

静态查找和动态查找
静态查找：
在查找过程中仅仅是执行“查找”的操作，即：（1）查看某特定的关键字是否在表中（判断性查找）；（2）检索某特定关键字数据元素的各种属性（检索性查找）。
动态查找：
查找的过程中对表的操作会多两个动作：（1）首先也有一个“判断性查找”的过程，如果某特定的关键字在表中不存在，则按照一定的规则将其插入表中；（2）如果已经存在，则可以对其执行删除操作。

无序查找和有序查找
无序查找：被查找数列有序无序均可
有序查找：被查找数列必须为有序数列

顺序查找

顺序查找适合于存储结构为顺序存储或链接存储的线性表，时间复杂度为O(n)

基本思想：从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。

平均查找长度分析：
查找成功的长度：ASL=1×(1×2×3×4×....×n)/n=(1+n)/2
查找不成功的长度：ASL=n

代码实现

int SequenceSearch(int a[], int value, int n)
{
    int i;
    for(i=0; i<n; i++)
        if(a[i]==value)
            return i;
    return -1;
}

折半查找

元素必须是有序的，如果是无序的则要先进行排序操作

基本思想：给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。

平均查找长度分析：
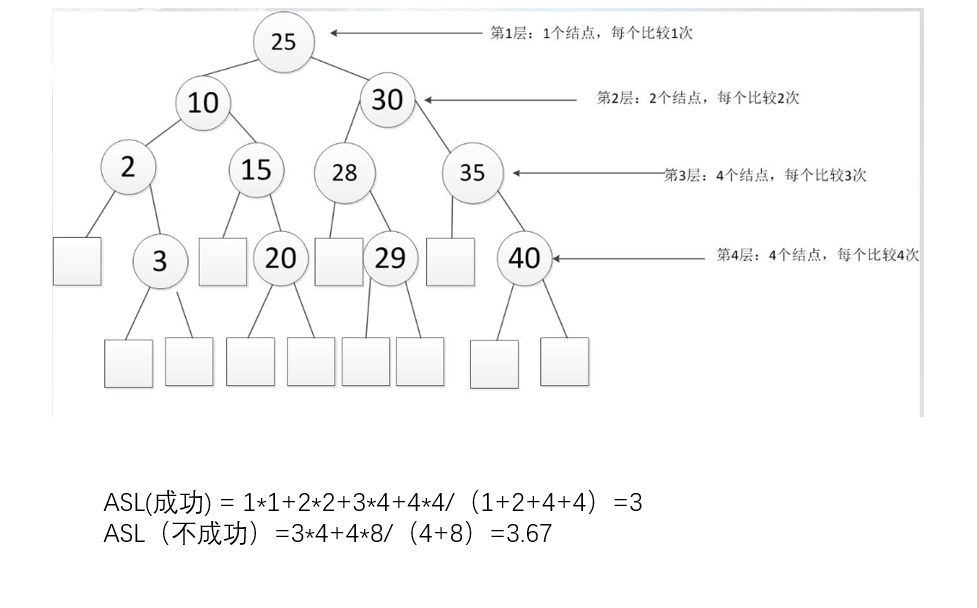
查找成功的长度：ASL= ΣPi×level(Ki) Pi为查找k的概率，level(Ki)为k对应内部结点的层次
查找不成功的长度：ASL= Σqi×(level(Ui)-1) qi表示查找属于Ei中关键字的概率，level(Ui)表示Ei对应外部结点的层次

代码实现

int BinarySearch1(int a[], int value, int n)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while(low<=high)
    {
        mid = (low+high)/2;
        if(a[mid]==value)
            return mid;
        if(a[mid]>value)
            high = mid-1;
        if(a[mid]<value)
            low = mid+1;
    }
    return -1;
}

int BinarySearch2(int a[], int value, int low, int high)
{
    int mid = low+(high-low)/2;
    if(low > high)
        return -1;
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return BinarySearch2(a, value, low, mid-1);
    if(a[mid]<value)
        return BinarySearch2(a, value, mid+1, high);
}

插值查找

适合表长较大，而关键字分布又比较均匀的查找表

基本思想：将查找点的选择改进为自适应选择，mid=low+(key-a[low])/(a[high]-a[low])*(high-low)
（1）如果与给定关键字相同，则查找成功，返回在表中的位置；
（2）如果给定关键字大，则更新左区间起始位置等于 mid + 1 ，即向右查找；
（3）如果给定关键字小，查找的值不在范围，直接返回；
（4）重复过程，直到找到关键字（成功）或区间为空集（失败）。

代码分析

int InsertionSearch(int a[], int value, int low, int high)
{
    int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return InsertionSearch(a, value, low, mid-1);
    if(a[mid]<value)
        return InsertionSearch(a, value, mid+1, high);
}

斐波那契查找

在斐波那契数列找一个等于略大于查找表中元素个数的数F[n]，将原查找表扩展为长度为Fn，完成后进行斐波那契分割，即F[n]个元素分割为前半部分F[n-1]个元素，后半部分F[n-2]个元素，找出要查找的元素在那一部分并递归，直到找到。斐波那契查找只适用于顺序表、有序数组。

基本思想：
斐波那契查找要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1；开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1)，
比较结果分为三种：
（1）相等，则mid位置的元素就是要查找的元素
（2）大于，则low=mid+1，k-=2；low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))=Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个。
（3）小于，则high=mid-1，k-=1；low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个。

代码实现

/*构造一个斐波那契数组*/   
void Fibonacci(int * F)  
{  
    F[0]=0;  
    F[1]=1;  
    for(int i=2;i<max_size;++i)  
        F[i]=F[i-1]+F[i-2];  
}  
  
/*定义斐波那契查找法*/    
int Fibonacci_Search(int *a, int n, int key)  //a为要查找的数组,n为要查找的数组长度,key为要查找的关键字  
{  
  int low=0;  
  int high=n-1;  
    
  int F[max_size];  
  Fibonacci(F);//构造一个斐波那契数组F   
  
  int k=0;  
  while(n>F[k]-1)//计算n位于斐波那契数列的位置  
      ++k;  
  
  int  * temp;//将数组a扩展到F[k]-1的长度  
  temp=new int [F[k]-1];  
  memcpy(temp,a,n*sizeof(int));  
  
  for(int i=n;i<F[k]-1;++i)  
     temp[i]=a[n-1];  
    
  while(low<=high)  
  {  
    int mid=low+F[k-1]-1;  
    if(key<temp[mid])  
    {  
      high=mid-1;  
      k-=1;  
    }  
    else if(key>temp[mid])  
    {  
     low=mid+1;  
     k-=2;  
    }  
    else  
    {  
       if(mid<n)  
           return mid; //若相等则说明mid即为查找到的位置  
       else  
           return n-1; //若mid>=n则说明是扩展的数值,返回n-1  
    }  
  }    
  delete [] temp;  
  return -1;  
}  

树表查找

• 二叉查找树
  性质：
  （1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  （2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  （3）任意节点的左、右子树也分别为二叉查找树。
  （4）对二叉查找树进行中序遍历，即可得到有序的数列。

  二叉查找树的具体操作，请看：查找、插入、删除结点

• 平衡二叉树
  性质：
  （1）每棵子树中的左子树和右子树的深度差不能超过 1；
  （2） 二叉树中每棵子树都要求是平衡二叉树；

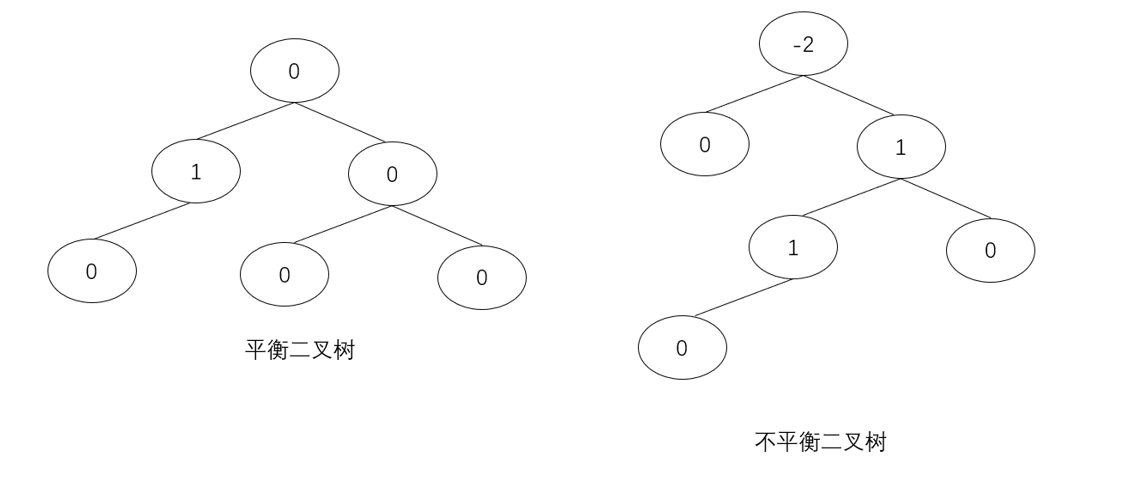
平衡二叉树的具体旋转调整，请看：单旋转、双旋转、删除、查找、插入

• 红黑树
  性质：
  （1）每个节点或者是黑色，或者是红色。
  （2）根节点是黑色。
  （3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
  （4）如果一个节点是红色的，则它的子节点必须是黑色的。
  （5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

  红黑树的具体操作，请看：旋转、添加、删除

分块查找

分块查找又称索引顺序查找，它是顺序查找的一种改进方法。

算法思想：将查找表分为若干个子块。块内元素可以无序，但块之间是有序的，即第一个块中的最小关键字小于第二个块中的所有记录的关键字，第二个块中的最大关键字小于第三个块中的所有记录的关键字，以此类推。在建立一个索引表，索引表中的每个元素含有各块的最大关键字和各块中第一个元素的地址，索引表按关键字有序排列。给定一个待查找的key，在查找这个key值位置时，会先去索引表中利用顺序查找或者二分查找来找出这个key所在块的索引开始位置，然后再根据所在块的索引开始位置开始查找这个key所在的具体位置。

过程：
1.确定要查找的关键字可能存在的具体块（子表）；
2.在具体的块中进行顺序查找。

查找性能分析：
分块查找算法的运行效率受两部分影响：查找块的操作和块内查找的操作。查找块的操作可以采用顺序查找，也可以采用折半查找（更优）；块内查找的操作采用顺序查找的方式。相比于折半查找，分块查找时间效率上更低一些；相比于顺序查找，由于在子表中进行，比较的子表个数会不同程度的减少，所有分块查找算法会更优。时间复杂度为O(log₂(m)+N/m)，m为分块的数量，N为主表元素的数量，N/m 就是每块内元素的数量。

ASL分析：
若在块内和索引表中均采用顺序查找，则平均查找长度为：ASL=(b+1)/2+(s+1)/2=(s2+2s+n)/(2s)　　［长度为n的查找表均匀的分为b块，每块有s个记录］
若对索引表采用折半查找时，则平均查找长度为：ASL=log２(b+1)-1+(s+1)/2

代码实现：

struct index    //定义块的结构
{
    int key;    //块的关键字
    int start;    //块的起始值
    int end;    //块的结束值
}index_table[4];    //定义结构体数组

int block_search(int key,int a[])    //自定义实现分块查找
{
    int i,j;
    i=1;
    while(i<=3&&key>index_table[i].key)    //确定在哪个块中
        i++;
    if(i>3)    //大于分得的块数，则返回0
        return 0;
    j=index_table[i].start;    //j等于块范围的起始值
    while(j<=index_table[i].end&&a[j]!=key)    //在确定的块内进行顺序查找
        j++;
    if(j>index_table[i].end)    //如果大于块范围的结束值，则说明没有要査找的数，j置0
        j = 0;
    return j;
}

哈希查找

Hash是一种典型以空间换时间的算法。根据键值（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

算法流程：
1）用给定的哈希函数构造哈希表；
2）根据选择的冲突处理方法解决地址冲突；常见的解决冲突的方法：拉链法和线性探测法。
3）在哈希表的基础上执行哈希查找。

哈希函数构造方法：

• 直接定址法：取关键字或关键字的某个线性函数值为散列地址。即hash(k) = k 或 hash(k) = a · k + b，其中a、b为常数（这种散列函数叫做自身函数）
• 数字分析法：假设关键字是以r为基的数，并且哈希表中可能出现的关键字都是事先知道的，则可取关键字的若干数位组成哈希地址。
• 平方取中法：取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况，取其中的哪几位也不一定合适，而一个数平方后的中间几位数和数的每一位都相关，由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
• 折叠法：将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）作为哈希地址。
• 随机数法：hash(k) = random(k) 生成随机数为哈希地址
• 除留余数法：取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 hash(k) = k mod p， p<=m。不仅可以对关键字直接取模，也可在折叠法、平方取中法等运算之后取模。对p的选择很重要，一般取素数或m，若p选择不好，容易产生冲突。

解决哈希冲突
开放定址法：先通过哈希函数进行判断，若是发生哈希冲突，就以当前地址为基准，根据再寻址的方法（探查序列），去寻找下一个地址，若发生冲突再去寻找，直至找到一个为空的地址为止。只要哈希表足够大，空的哈希地址总是能找到，然后将记录插入。
开放定址法创建哈希表

typedef int KeyType;		//关键字类型
typedef char * InfoType;	//其他数据类型
typedef struct node
{
	KeyType key;			//关键字域
	InfoType data;			//其他数据域
	int count;				//探查次数域
} HashTable[MaxSize];		//哈希表类型
void InsertHT(HashTable ha, int& n, KeyType k, int p)
{
	int adr, i;

	adr = k % p;
	if (ha[adr].count == 0)
	{
		ha[adr].key = k;
		ha[adr].count = 1;
	}
	else
	{
		i = 1;
		while (ha[adr].count != 0)
		{
			adr = (adr + 1) % p;
			i++;
		}
		ha[adr].key = k;
		ha[adr].count = i;
	}
	n++;
}

拉链法：采用链表的数据结构来去存取发生哈希冲突的输入域的关键字（也就是被哈希函数映射到同一个位桶上的关键字）。
拉链法创建哈希链

typedef struct Node
{
	TYPE data;
	struct Node * next;
}Node;
Node * node[HASH_SIZE];

void insert(TYPE data)
{
	int index = hash(data);

	Node * new_node = malloc(sizeof(Node));
	if(new_node == NULL)
		printf("memory alloc error"),exit(EXIT_FAILURE);
	new_node->data = data;
	new_node->next = NULL;

	if(node[index] != NULL)
		new_node->next = node[index];
	node[index] = new_node;
}

拉链法和开放定址法对比
（1）拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
（2）由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
（3）开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
（4）在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。

拉链法和开放定址法ASL分析：

动态查找：二叉搜索树

性质

（1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）任意节点的左、右子树也分别为二叉查找树。
（4）对二叉查找树进行中序遍历，即可得到有序的数列。

查找结点

和根节点进行比较，如果等于根节点，则返回。如果小于根节点，则在根节点的左子树进行查找。如果大于根节点，则在根节点的右子树进行查找。

Position Find(ElementType x, SearchTree t)
{
    if (t == NULL) {
        return NULL;
    } else if (x < t->element) {
        return Find(x, t->left);
    } else if (x > t->element) {
        return Find(x, t->right);
    } else {
        return t;
    }
}

查找最大值和最小值

查找最小值：从根开始，如果有左儿子，则向左进行。直到左儿子为空，则当前节点为最小值。
查找最大值：从根开始，如果有右儿子，则向右进行。直到右儿子为空，则当前节点为最大值。

Position FindMin(SearchTree t)
{
    if (t == NULL) {
        return NULL;
    } else if (t->left == NULL) {
        return t;
    } else {
        return FindMin(t->left);
    }
}

Position FindMax(SearchTree t)
{
    if (t == NULL) {
        return NULL;
    }

    while (t->right != NULL)
    {
        t = t->right;
    }
    return t;
}

插入结点

如果待插入的数据比当前节点的数据大，并且当前节点的右儿子为空，则将待插入的节点插到右儿子位置上。如果右儿子不为空，则再递归的遍历右儿子。如果小于当前节点，则对左儿子做处理。

BST Insert(ElementType x, SearchTree t)
{
    if (t == NULL) {
        /* 插入第一个节点 */
        t = (SearchTree)malloc(sizeof(struct TreeNode));
        if (t == NULL) {
            return NULL;
        }
        t->element = x;
        t->left = NULL;
        t->right = NULL;
    } else if (x < t->element) {
        t->left = Insert(x, t->left);
    } else if (x > t->element) {
        t->right = Insert(x, t->right);
    }
    return t;
}

删除结点

• 1、待删除的节点是一个叶子节点，即它没有左右儿子。此时只要将它的父节点指向NULL即可。
• 2、如果节点有一个儿子，则该节点可以在其父节点调整指针绕过该节点后删除。
• 3、如果有两个儿子，一般的删除策略是用其右子树中最小的数据代替该节点的数据并递归地删除那个节点。因为右子树中最小地节点不可能有左儿子(如果有，则说明不是最小的)，所以第二次删除更容易。(其实也就是将有两个儿子的情况转为容易处理的情况1或者2)。

BST Delete(ElementType x, SearchTree t)
 {
     Position tmp;
     if (t == NULL) {
         return NULL;
     }
     if (x < t->element) {
         t->left = Delete(x, t->left);
     } else if (x > t->element) {
         t->right = Delete(x, t->right);
     } else if (t->left && t->right) {
         tmp = FindMin(t->right);
         t->element = tmp->element;
         t->right = Delete(t->element, t->right);
     } else {
         tmp = t;
         if (t->left) {
             t = t->left;
         } else if (t->right) {
             t = t->right;
         }
         free(tmp);
         tmp = NULL;
     }
     return t;
 }

建树

SearchTree MakeEmpty(SearchTree t)
{
    if (t != NULL) {
        MakeEmpty(t->left);
        MakeEmpty(t->right);
        free(t);
        t = NULL;
    }
    return NULL;
}

AVL树

AVL树的定义

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

• LL型：在A结点左子树根结点的左子树插入结点，导致A结点平衡因子由1变2。进行一次顺时针旋转；将原根结点的左孩子作为新生成树的根结点，将左孩子的右子树作为原树根结点的左孩子。
• RR型：在A结点右子树根结点的右子树插入结点，导致A结点平衡因子由-1变-2。 进行一次逆时针旋转；将原根结点的右孩子作为新生成树的根结点，将右孩子的左子树作为原树根结点的右孩子。
• LR型：在A结点左子树根结点的右子树插入结点，导致A结点平衡因子由1变2。先逆时针旋转一次，后顺时针旋转一次；将新插入的部分作为此插入结点父节点的右孩子，逆时针旋转一次，将此结点作为此子树的根结点，将其原父节点作为此结点的左孩子，再将此结点的右孩子作为原树根结点的左孩子，顺时针旋转一次，将此结点作为整个树的根结点，将原根结点作为新生成树的右孩子。
• RL型：在A结点右子树根结点的左子树插入结点，导致A结点平衡因子由-1变-2。先顺时针旋转一次，后逆时针旋转一次；将新插入的部分作为此插入结点父节点的左孩子，顺时针旋转一次，将此结点作为此子树的根结点，将其原父节点作为此结点的右孩子，再将此结点的左孩子作为原树根结点的右孩子，逆时针旋转一次，将此结点作为整颗树的根结点，将原根结点作为新生成树的左孩子。

LL调整

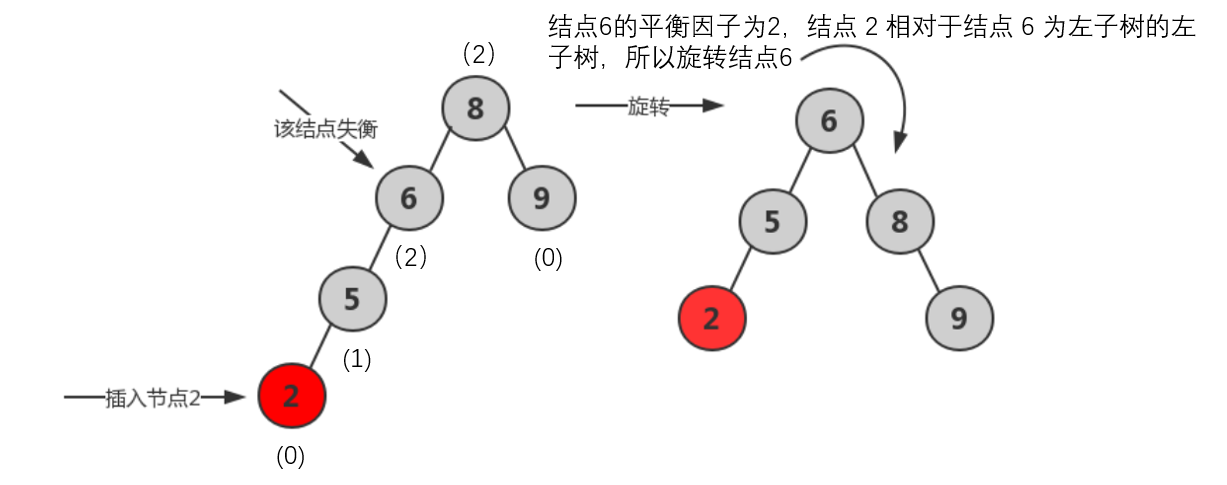
 void LL(AVLNode** t) 
    {
        if (t != nullptr)
        {
            AVLNode* tmpPtr = (*t)->left;
            (*t)->left = tmpPtr->right;    //t左子树的右子树作为t的左子树
            tmpPtr->right = *t;
            *t = tmpPtr;
        }
    }

RR调整

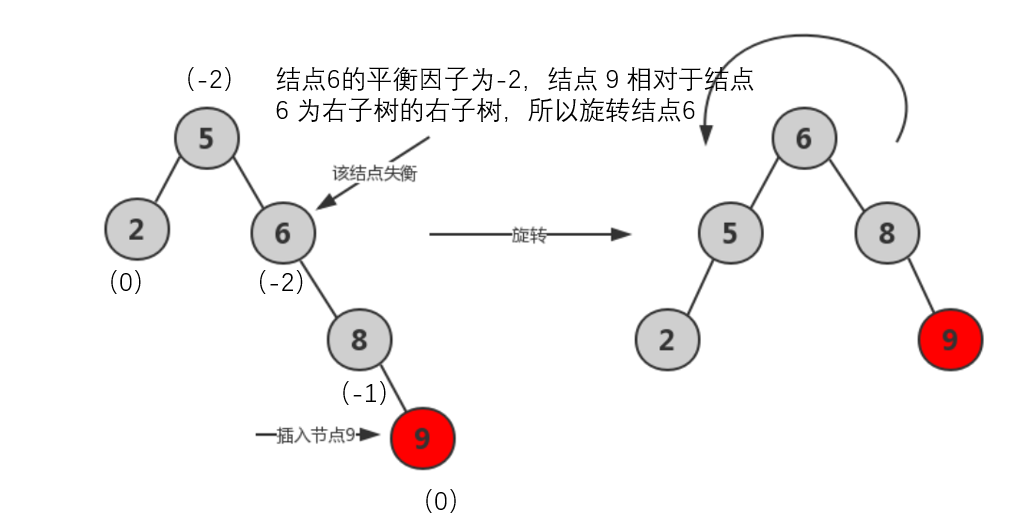
void RR(AVLNode** t)
    {
        if (t != nullptr) 
        {
            AVLNode* tmpPtr = (*t)->right;
            (*t)->right = tmpPtr->left;
            tmpPtr->left = *t;
            *t = tmpPtr;
        }
    }

LR调整

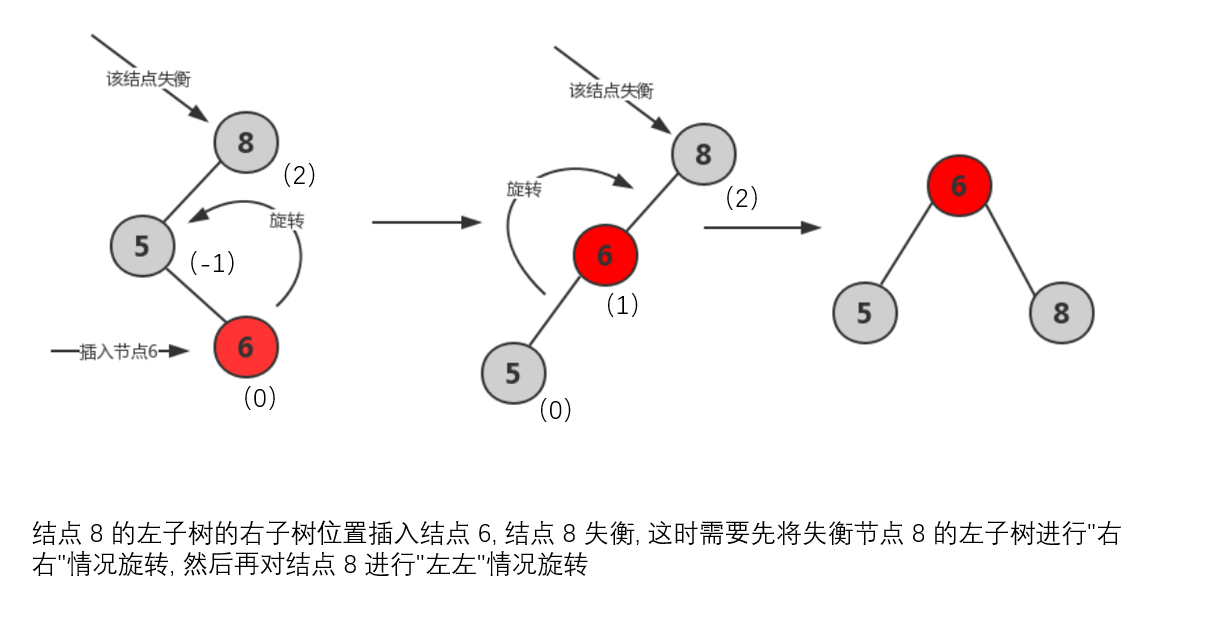
void LR(AVLNode** t) 
    {
        RR(&(*t)->left);
        LL(t);
    }

RL调整

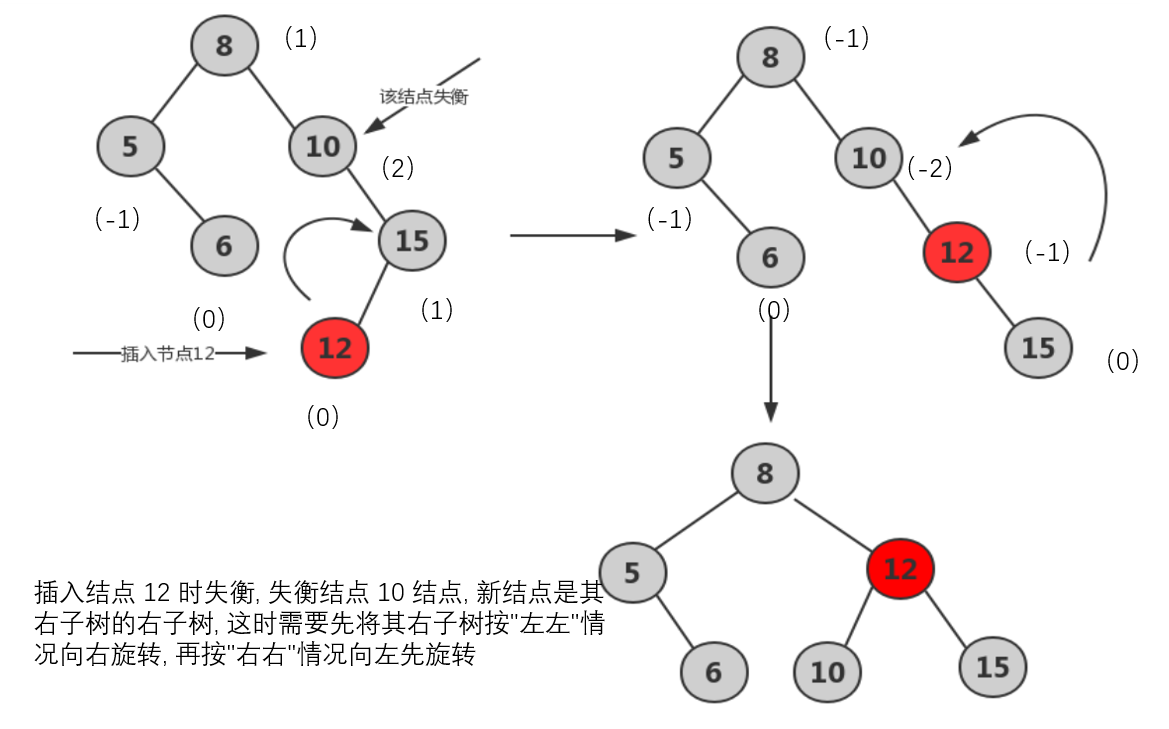
void RL(AVLNode** t) 
    {
        LL(&(*t)->right);
        RR(t);
    }

删除结点

int findMaxKeyInLef(AVLNode* node) 
    {
        if (node == nullptr)
            return 0;
        else if (node->right == nullptr)
            return node->val;
        return findMaxKeyInLef(node->right);
    }
    AVLNode* delNodeFromTree(AVLNode** node, int val) 
    {
        if (node == nullptr) 
            return nullptr;
        else if (val < (*node)->val)
        {
            (*node)->left = delNodeFromTree(&(*node)->left, val);
            //判断是否失衡,删了左子树一个结点,所以判断右子树高度是否过高
            if ((getHeight((*node)->right) - getHeight((*node)->left)) > 1) 
                //右子树的左子树高度比右子树的右子树更高,相当于给右子树的右子树插入了新节点,相当于"右右"情况
                if (getHeight((*node)->right->left) > getHeight((*node)->right->right))
                    RL(node);
                else 
                    RR(node);
            return (*node);
        }
        else if (val > (*node)->val)
        {
            (*node)->right = delNodeFromTree(&(*node)->right, val);
            //判断是否失衡,删了右子树一个结点,所以判断左子树高度是否过高
            if ((getHeight((*node)->left) - getHeight((*node)->right)) > 1) 
                //左子树的左子树高度比右子树的右子树更高,相当于给左子树的左子树插入了新节点,相当于"左左"情况
                if (getHeight((*node)->left->left) > getHeight((*node)->left->right))
                    LL(node);
                else 
                    LR(node);
            return (*node);
        }
        else if (val == (*node)->val)
        {
            //如果是叶子节点
            if ((*node)->left == nullptr && (*node)->right == nullptr) 
            {
                delete (*node);
                (*node) = nullptr;
                return (*node);;
            }
            //如果左子树非空,将右子树续接到父节点
            else if ((*node)->left != nullptr) 
            {
                AVLNode* tmp = (*node)->left;
                delete (*node);
                return tmp;
            }
            //如果右子树非空,将左子树续接到父节点
            else if ((*node)->right != nullptr) 
            {
                AVLNode* tmp = (*node)->right;
                delete (*node);
                return tmp;
            }
            //左右子树皆非空
            else 
            {
                //寻找左子树中最大节点,即左子树中最右节点
                //(也可以寻找右子树中最小节点,即右子树中最左节点)
                int maxVal = findMaxKeyInLef((*node)->left);
                //交换这两个节点
                (*node)->val = maxVal;
                //删除那个用来交换的节点
                (*node)->left = delNodeFromTree(&(*node)->left, maxVal);
                return *node;
            }
        }
    }

插入结点

 void insertNode(AVLNode** t, int v) 
    {   
        //插入结点,使用二级指针改变父节点左右子树指针指向
        if (*t == nullptr) 
            *t = new AVLNode(v); 
        else if (v < (*t)->val) 
        {
            insertNode(&((*t)->left), v);
            int leftH = getHeight((*t)->left);
            int rightH = getHeight((*t)->right);
            //插入到左子树,肯定是左子树高度更高,判断这时平衡因子是否大于1
            if ((leftH - rightH) > 1) 
            {
                if (v < (*t)->left->val) 
                    LL(t);
                else
                    LR(t);
            }
        }
        else if (v > (*t)->val) 
        {
            insertNode(&((*t)->right), v);
            int leftH = getHeight((*t)->left);
            int rightH = getHeight((*t)->right);
            if ((rightH - leftH) > 1) 
            {
                if (v > (*t)->right->val)
                    RR(t);
                else 
                    RL(t);
            }
        }
        else 
            return ;
    }

最大值结点

template <typename T>
AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const
{
    if (t == NULL)
        return NULL;
    if (t->right == NULL)
        return t;
    return FindMax(t->right);
}

最小值结点

template <typename T>
AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const
{
    if (t == NULL)
        return NULL;
    if (t->left == NULL)
        return t;
    return FindMin(t->left);
}

求树的高度

template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T> *t)
{
    if (t == NULL)
        return -1;
    else
        return t->height;
}

B-树和B+树和B*树

B-树

B-树多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B-树的定义：

• 每个节点最多有m-1个关键字（可以存有的键值对）。
• 根节点最少可以只有1个关键字。
• 非根节点至少有m/2个关键字。
• 每个节点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
• 所有叶子节点都位于同一层，或者说根节点到每个叶子节点的长度都相同。
• 每个节点都存有索引和数据，也就是对应的key和value。

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已是叶子结点；

特点:

• 关键字集合分布在整颗树中；
• 任何一个关键字出现且只出现在一个结点中；
• 搜索有可能在非叶子结点结束；
• 其搜索性能等价于在关键字全集内做一次二分查找；
• 自动层次控制；

一个m阶的B树具有如下几个特征：

• 根结点至少有两个子女。
• 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
• 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
• 所有的叶子结点都位于同一层。
• 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

B+树

B+树是一种树数据结构，是一个n叉树，每个节点通常有多个孩子，一棵B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩子节点的节点。在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

特点：

• 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
• 不可能在非叶子结点命中；
• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
• 更适合文件索引系统；

一个m阶的B+树具有如下几个特征：

• 有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
• 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
• 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

B+树的优势：

• 单一节点存储更多的元素，使得查询的IO次数更少。
• 所有查询都要查找到叶子节点，查询性能稳定。
• 所有叶子节点形成有序链表，便于范围查询。

B×树

B×树在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；
B×树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

B-树、B+树的区别

• 关键字的数量不同：B+树中分支结点有m个关键字，其叶子结点也有m个，其关键字只是起到了一个索引的作用，但是B树虽然也有m个子结点，但是其只拥有m-1个关键字。
• 存储的位置不同：B+树中的数据都存储在叶子结点上，也就是其所有叶子结点的数据组合起来就是完整的数据，但是B树的数据存储在每一个结点中，并不仅仅存储在叶子结点上。
• 分支结点的构造不同：B+树的分支结点仅仅存储着关键字信息和儿子的指针（这里的指针指的是磁盘块的偏移量），也就是说内部结点仅仅包含着索引信息。
• 查询不同：B树在找到具体的数值以后，则结束，而B+树则需要通过索引找到叶子结点中的数据才结束，也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。
• B树只能支持随机检索，而B+树是有序的树，既能支持随机检索，又能支持顺序检索。

B-树、B+树的基本操作

插入
在插入新的数据元素时，首先向最底层的某个非终端结点中添加，如果该结点中的关键字个数没有超过 m-1，则直接插入成功，否则生成一新结点，把原结点上的关键字和k按升序排序后，从中间位置把关键字（不包括中间位置的关键字）分成两部分。左部分所含关键字放在旧结点中，右部分所含关键字放在新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过（m-1），则要再分裂，再往上插。直至这个过程传到根结点为止。

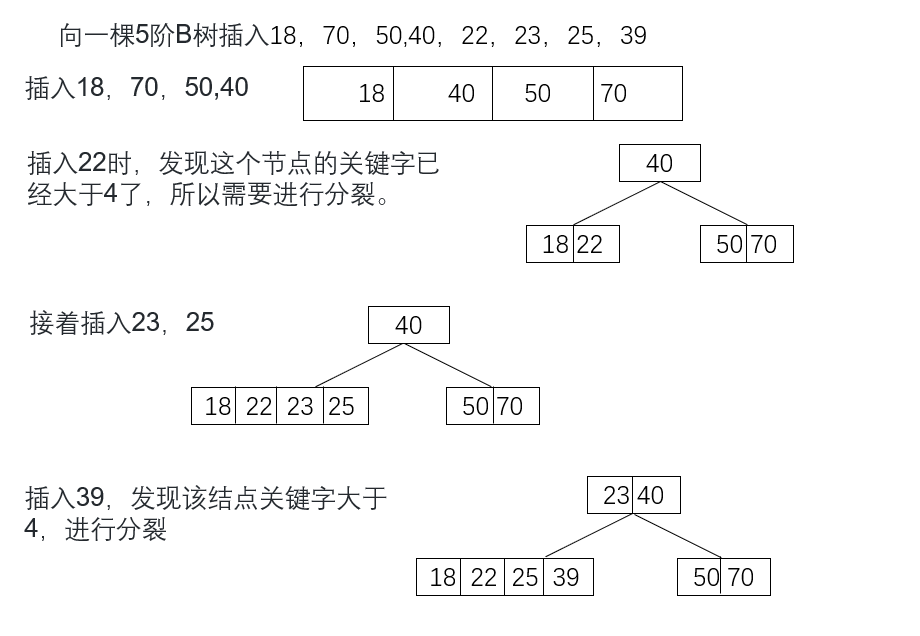
删除
首先找到要删除的关键码所在结点，假设所删关键码为非终端结点中Ki，则可用指针Ai所指子树中最小关键码Y代替Ki，然后在相应终端结点中删去Y，这样就转为删除终端结点中的关键码的问题了。
删除终端节点中关键码：

• 被删关键码所在结点中的关键码个数>=[m/2],说明删去该关键字后该结点仍满足B-树的定义。这种情况最为简单，只需从该结点中直接删去关键字即可。
• 被删关键码所在结点中关键码个数n=[m/2]-1，说明删去该关键字后该结点将不满足B-树的定义，需要调整。调整过程为：如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右（左）兄弟结点中的关键字数目大于[m/2]-1。则可将右（左）兄弟结点中最小（大）关键字上移至双亲结点。而将双亲结点中小（大）于该上移关键字的最大（小）关键字下移至被删 关键字所在结点中。
• 被删关键码所在结点和其相邻的左右兄弟节点中的关键码个数均等于[m/2]-1，左右兄弟都不够借。需把要删除关键字的结点与其左（或右）兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后，该结点中剩余的关键字加指针，加上双亲结点中的关键字Ki一起，合并到Ai（即双亲结点指向该删除关键字结点的左（右）兄弟结点的指针）所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于[m/2]-1，则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。

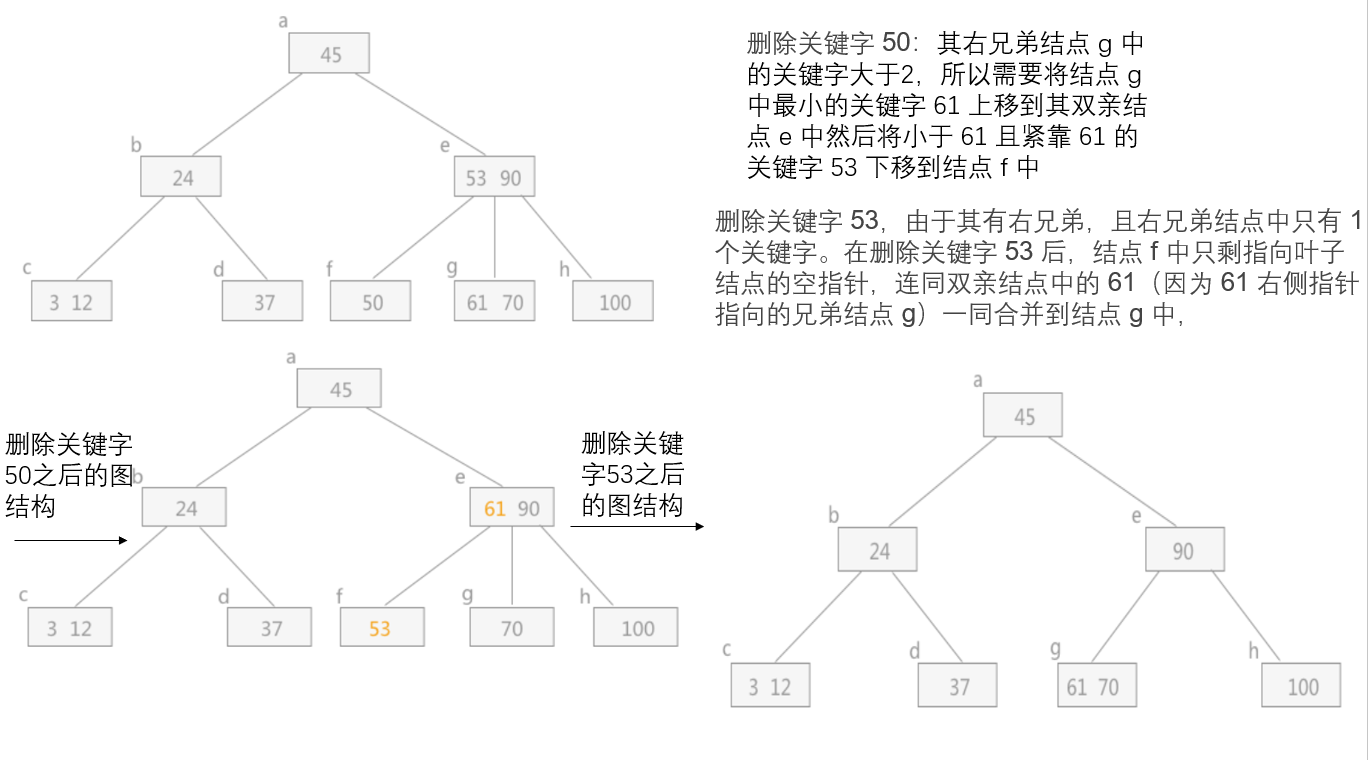
散列查找

Hash是一种典型以空间换时间的算法。根据键值（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

散列函数的构造方法

直接定址法
取关键字的某个线性函数值为散列地址，hash(k)=a×k+b(a,b为常数)

优点：简单、均匀，也不会产生冲突。
缺点：需要事先知道关键字的分布情况，适合查找表较小且连续的情况。

数字分析法
假设关键字是以r为基的数，并且哈希表中可能出现的关键字都是事先知道的，则可取关键字的若干数位组成哈希地址。

若容易发生冲突，可以对抽取出来 的数字再进行反转、右环位移等操作，提供一个能够尽量合理地将关键字分配到散列表的各个位置的散列函数。

适合关键字位数比较大的情况或者事先知道关键字的分布且关键字的若干位分布比较均匀

平方取中法
取关键字平方的中间位数作为散列地址。

假设关键字是 4321，那么它的平方就是 18671041，抽取中间的 3 位就可以是 671，也可以是 710，用做散列地址。

适合于不知道关键字的分布，而位数又不是很大的情况

折叠法
将关键字从左到右分割成位数相等的几部分，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址

不需要知道关键字的分布，适合关键字位数较多的情况

除留余数法
对于散列表长为m的散列函数公式为：hask(k)=k mod p(p<=m)。通常p为小于或等于表长（最好接近m）的最小质数或不包含小于20质因子的合数。

随机数法
选择一个随机数，取关键字的随机函数值为它的散列地址。hask(key) = random(key)

适合于关键字的长度不等

处理散列冲突的方法

开放定址法
开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

• 线性探测法
  HASHi(k)=(HASH(k)+Di) mod p (Di=1,2...m-1)

• 二次探测法
  di = 1²,-1²,2²,-2²,3²,-3²,...

• 伪随机探测法
  di = 伪随机数序列（任意的数）
  优点：避免了“二次聚集”现象。
  缺点：不能保证一定可以找到一个新的散列地址。

再散列函数法
对于散列表来说，可以事先准备多个散列函数。Fi(k)=RHi(k),(i=1,2,3,...,k),RHi 就是不同的散列函数。

每当发生散列地址冲突时，就换一个散列函数计算，直到碰撞不再发生。 这种方法能够使得关键字不产生聚集，但相应地也增加了计算的时间。

链地址法
将所有关键字为同义词的记录存储在一个单链表中，称这种表为同义词子表，在散列表中只存储所有同义词子表前面的指针。

链地址法不存在什么冲突换地址的问题，无论有多少个冲突，都只是在当前位置给单链表增加结点的问题。 链地址法对于可能会造成很多冲突的散列函数来说，提供了绝不会出现找不到地址的保证。当然，这也就带来了查找时需要遍历单链表的性能损耗。

公共溢出区法
为所有冲突的关键字记录建立一个公共的溢出区来存放。

散列表的性能分析

如果没有冲突，散列查找是所介绍过的查找中效率最高的，时间复杂度为O(1)。
散列查找的平均查找长度取决于三大因素

• 散列函数是否均匀
  散列函数的好坏直接影响着出现冲突的频繁程度，但是，不同的散列函数对同一组随机的关键字，产生冲突的可能性是相同的。
• 处理冲突的方法
  相同的关键字、相同的散列函数，但处理冲突的方法不同，会使得平均查找长度不同。如线性探测处理冲突可能会产生堆积，显然就没有二次探测好，而链地址法处理冲突不会产生任何堆积，因而具有更好的平均查找性能。
• 散列表的装填因子
  装填因子a = 填入表中的记录个数/散列表长度。a标志着散列表的装满的程度。当填入的记录越多，a就越大，产生冲突的可能性就越大。也就说，散列表的平均查找长度取决于装填因子，而不是取决于查找集合中的记录个数。

散列表的ASL分析

散列表代码

结构体定义

typedef int KeyType;		//关键字类型
typedef char * InfoType;	//其他数据类型
typedef struct node
{
	KeyType key;			//关键字域
	InfoType data;			//其他数据域
	int count;				//探查次数域
} HashTable[MaxSize];		//哈希表类型

哈希表查找

int SearchHT(HashTable ha, int p, KeyType k)
{
	int i = 0, adr;

	adr = k % p;
	if (ha[adr].count == 0)
		return -1;
	else
	{
		if (ha[adr].key == k)
			return adr;
		else
		{
			uns_count++;
			while (1)
			{
				adr = (adr + 1) % p;
				uns_count++;
				if (ha[adr].count == 0)
					return -1;
				if (ha[adr].key == k)
					return adr;
			}
		}
	}		
}

创建哈希表

void InsertHT(HashTable ha, int& n, KeyType k, int p)
{
	int adr, i;

	adr = k % p;
	if (adr == NULLKEY || adr == DELKEY)
	{
		ha[adr].key = k;
		ha[adr].count = 1;
	}
	else
	{
		i = 1;
		while (ha[adr].count != 0)
		{
			adr = (adr + 1) % p;
			i++;
		}
		ha[adr].key = k;
		ha[adr].count = i;
	}
	n++;
}
void CreateHT(HashTable ha, KeyType x[], int n, int m, int p)
{
	int i, count = 0;
	for (i = 0; i < m; i++)
		ha[i].count = 0;
	for (i = 0; i < n; i++)
		InsertHT(ha, count, x[i], p);
}

哈希表删除

int DeleteHT(HashTable ha,int p,int k,int &n)
{
    int adr;
    adr=SearchHT(ha,p,k);
    
   if(adr!=-1)
   {
      ha[adr].key=DELKEY;
      n--;
     return 1;
   }
   else 
      return 0;
} 

哈希链结构体

typedef struct ArcNode
{
    int data; // 元素值 
    struct ArcNode * Next; 
}ArcNode, *pArcNode;

哈希链查找

pArcNode Search_Hash(HashList &hash,int key ,int adr)
{
   pArcNode temp;

   temp=hash[adr]->next;
   
   while(temp!=NULL)
   {
      if(temp->data==key)
      {
            break;
      }
      temp=temp->next;
   }
   return temp;
}

创建哈希链

void CreateHT(pArcNode ht[], KeyType x[], int n, int m, int p)
{
      for (i = 0; i < n; i++)
            Insert(ht, num, id, len);
}
void Insert(pArcNode ht[], char num[], int id, int len)
{
	HashTable node, temp;
	int flag = 1;

	temp = ht[id]->next;
	while (temp != NULL)
	{
		if (strcmp(temp->id, num) == 0)
		{
                        //插入的是同一关键字做什么操作
                        flag=0;
		}
		temp = temp->next;
	}
	temp = ht[id];
	if (flag == 1)
	{
		node = new HashNode;
		node->len = len;
		strcpy(node->id, num);
		node->next = NULL;
		node->next = temp->next;
		temp->next = node;
	}
}

直接插入排序算法

直接插入排序算法：在添加新的记录时，使用顺序查找的方式找到其要插入的位置，然后将新记录插入。

直接插入排序法过程

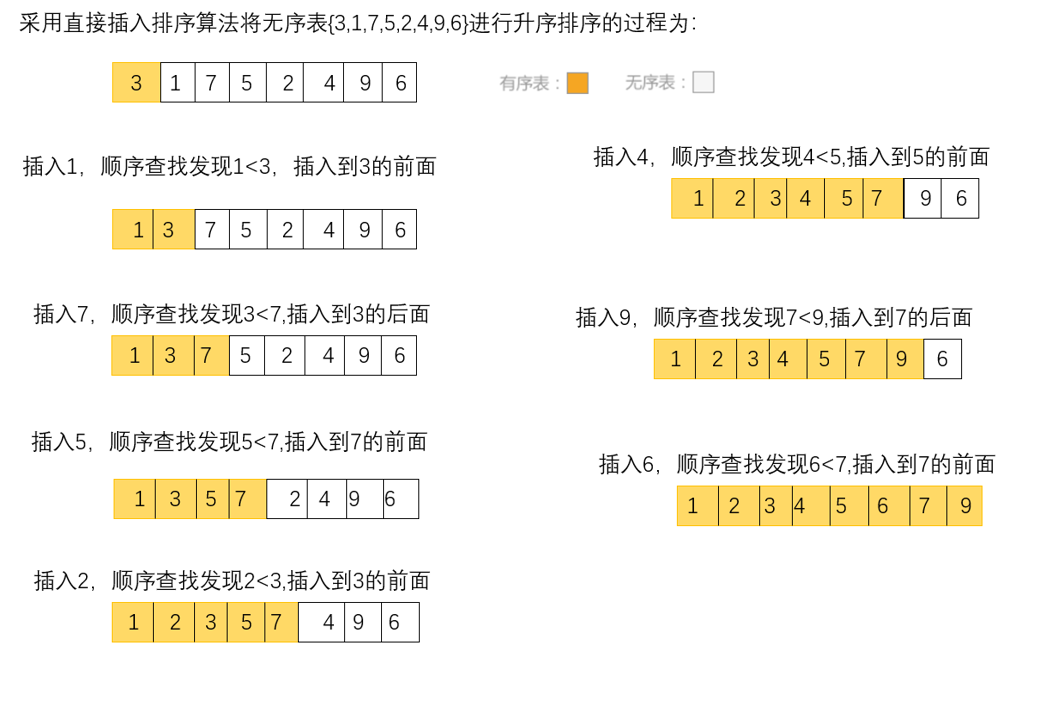
代码实现

//直接插入排序函数
void InsertSort(int a[], int n)
{
    for(int i= 1; i<n; i++){
        if(a[i] < a[i-1]){//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
            int j= i-1;
            int x = a[i];
            while(j>-1 && x < a[j]){  //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
                a[j+1] = a[j];
                j--;
            }
            a[j+1] = x;      //插入到正确位置
        }
        print(a,n,i);//打印每次排序后的结果
    }
}

希尔排序算法

希尔排序是在直接插入排序的基础上做的改进，也就是将寒排序的序列按固定增量分成若干组，等距者在同二组中，然后再在组内进行直接插入排序。这里面的固定增量从 n/2 开始，以后每次缩小到原来的一半。

希尔排序法过程

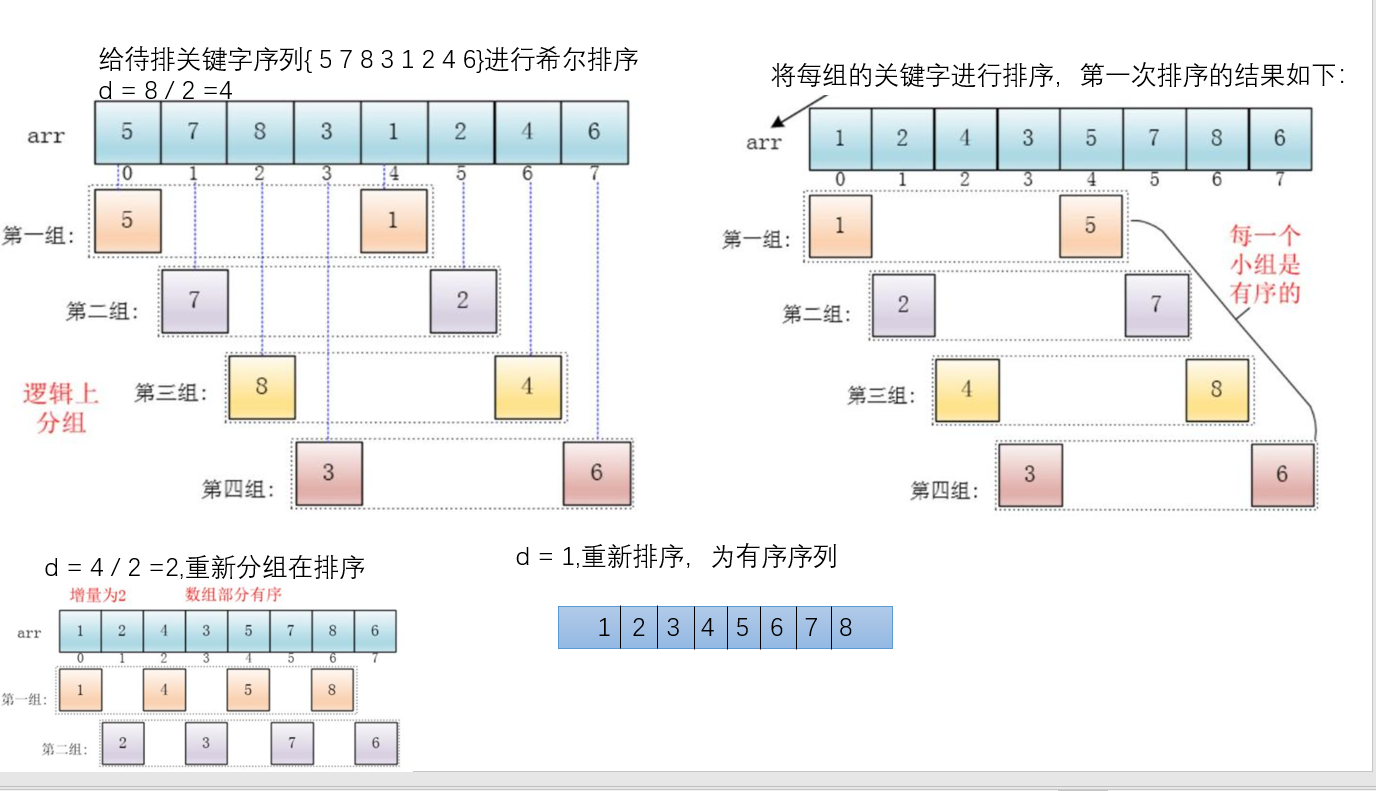
代码实现

int shsort(int s[], int n)    /* 自定义函数 shsort()*/
{
    int i,j,d;
    d=n/2;    /*确定固定增虽值*/
    while(d>=1)
    {
        for(i=d+1;i<=n;i++)    /*数组下标从d+1开始进行直接插入排序*/
        {
            s[0]=s[i];    /*设置监视哨*/
            j=i-d;    /*确定要进行比较的元素的最右边位置*/
            while((j>0)&&(s[0]<s[j]))
            {
                s[j+d]=s[j];    /*数据右移*/
                j=j-d;    /*向左移d个位置V*/
            }
            s[j + d]=s[0];    /*在确定的位罝插入s[i]*/
        }
        d = d/2;    /*增里变为原来的一半*/
    }
return 0;
}

快速排序算法

快速排序是冒泡排序的一种改进，主要的算法思想是在待排序的 n 个数据中取第一个数据作为基准值，将所有记录分为 3 组，使第一组中各数据值均小于或等于基准值，第二组做基准值的数据，第三组中各数据值均大于或等于基准值。这便实现了第一趟分割，然后再对第二组和第兰组分别重复上述方法，依次类推，直到每组中只有一个记录为止。

快排算法思想

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

• 分解：
  　在R[low..high]中任选一个记录作为基准(Pivot)，以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high]，并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key，右边的子区间中所有记录的关键字均大于等于pivot.key，而基准记录pivot则位于正确的位置(pivotpos)上，它无须参加后续的排序。
  注意：
  　划分的关键是要求出基准记录所在的位置pivotpos。划分的结果可以简单地表示为(注意pivot=R[pivotpos])：
  　R[low..pivotpos-1].keys≤R[pivotpos].key≤R[pivotpos+1..high].keys
  其中low≤pivotpos≤high。
• 求解：
  　 通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。
• 组合：
  　因为当"求解"步骤中的两个递归调用结束时，其左、右两个子区间已有序。对快速排序而言，"组合"步骤无须做什么，可看作是空操作。

快排算法过程

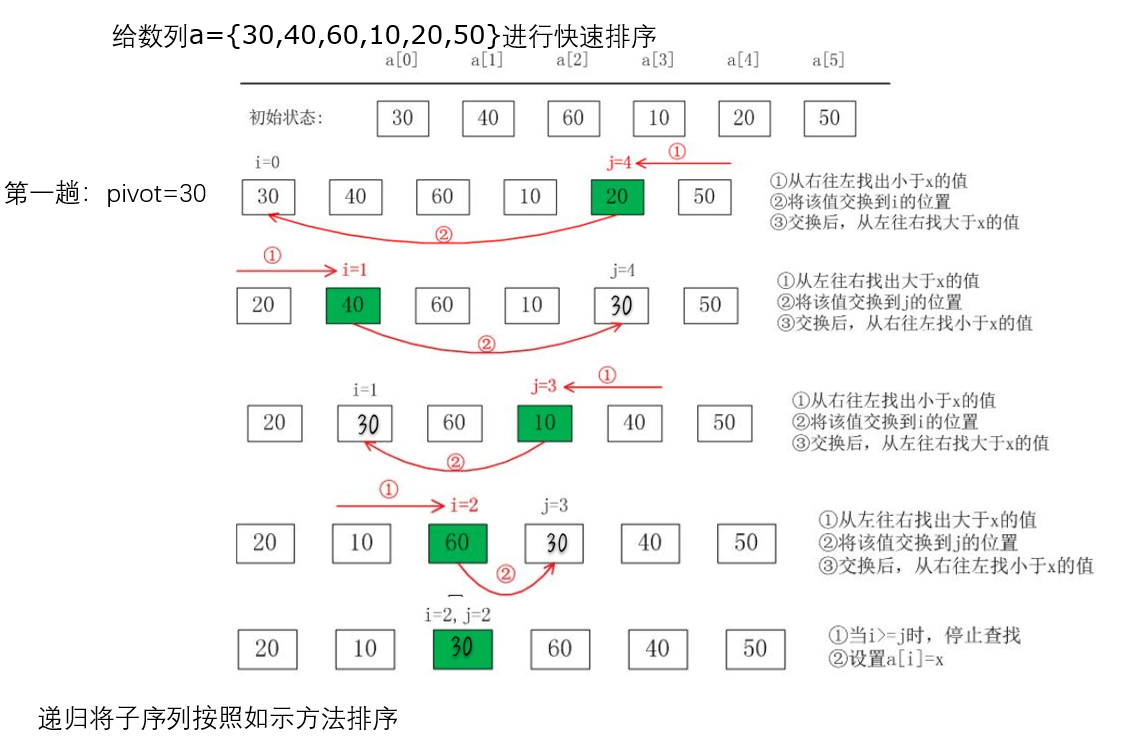
代码实现

void quickSort(int a[],int left,int right)
{
　　int i=left;
　　int j=right;
　　int temp=a[left];
　　if(left>=right)
　　　　return;
　　while(i!=j)
　　{
　　　　while(i<j&&a[j]>=temp) 
　　　　j--;
　　　　if(j>i)
　　　　　　a[i]=a[j];//a[i]已经赋值给temp,所以直接将a[j]赋值给a[i],赋值完之后a[j],有空位
　　　　while(i<j&&a[i]<=temp)
　　　　i++;
　　　　if(i<j)
　　　　　　a[j]=a[i];
　　}
　　a[i]=temp;//把基准插入,此时i与j已经相等R[low..pivotpos-1].keys≤R[pivotpos].key≤R[pivotpos+1..high].keys
　　quickSort(a,left,i-1);/*递归左边*/
　　quickSort(a,i+1,right);/*递归右边*/
}

归并排序算法

归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略。

• 算法复杂度：
  最好情况：O(nlogn)
  最坏情况：O(nlogn)
  平均情况：O(nlogn)
  空间复杂度：O(n)
• 算法稳定性：稳定

归并算法实现过程

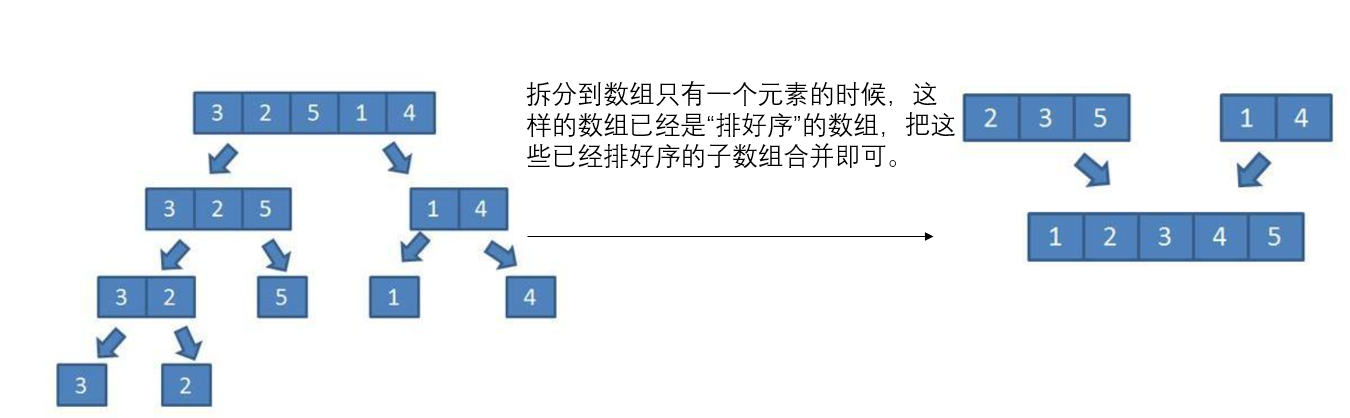
代码实现

int merge_sort(int r[],int s[],int m,int n)
{
    int p;
    int t[20];
    if(m==n)
        s[m]=r[m];
    else
    {
        p=(m+n)/2;
        merge_sort(r,t,m,p);    //递归调用merge_soit()函数将r[m]〜r[p]归并成有序的t[m]〜t[p]
        merge_sort(r,t,p+1,n);    //递归一调用merge_sort()函数将r[p+l]〜r[n]归并成有序的t[p+l]〜t[n]
        merge(t,s,m,p,n);    //调用函数将前两部分归并到s[m]〜s[n】*/
    }
    return 0;
}

堆排序算法

堆排序是一种树形选择排序，在排序过程中可以把元素看成是一颗完全二叉树，每个节点都大（小）于它的两个子节点，当每个节点都大于等于它的两个子节点时，就称为大顶堆，也叫堆有序； 当每个节点都小于等于它的两个子节点时，就称为小顶堆。

堆排序算法实现过程

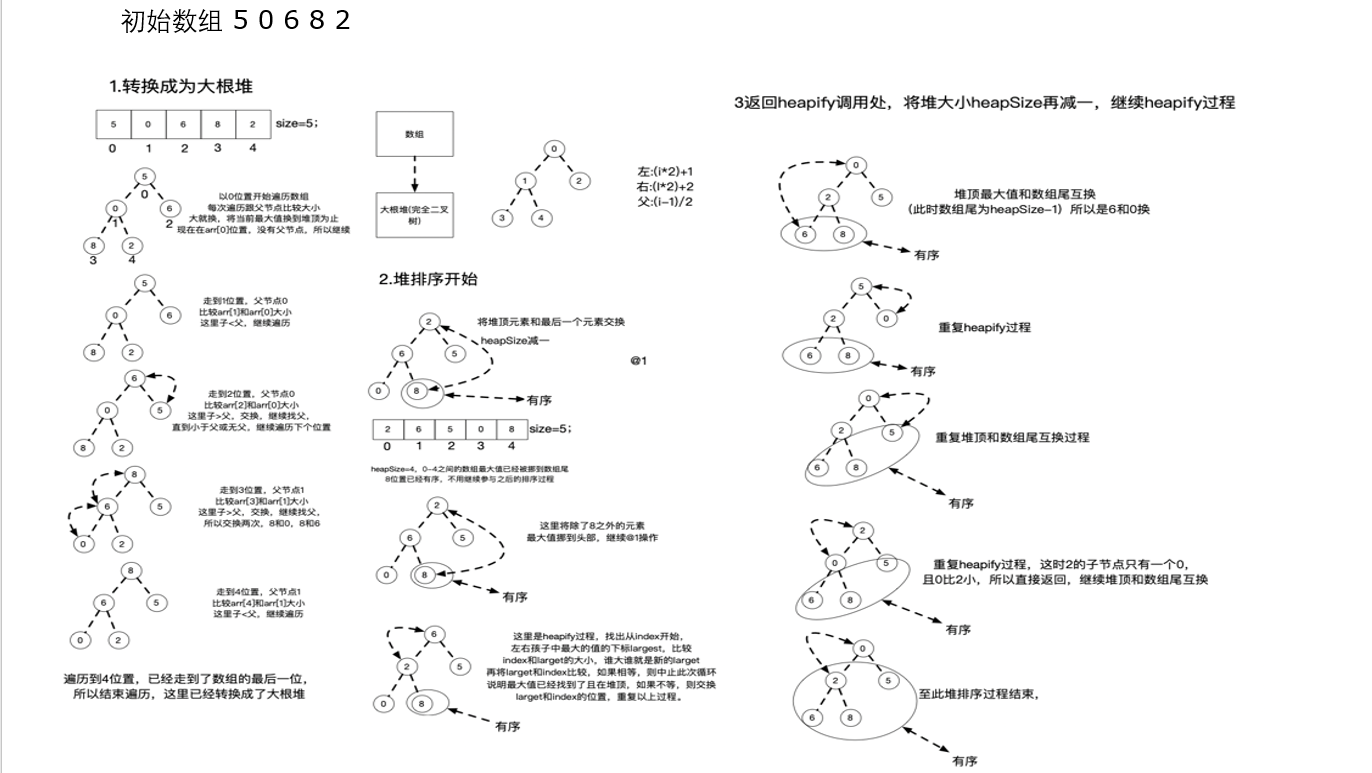
代码实现

int c=0; //记录交换次数
  
/*heapadjust()函数的功能是实现从a[m]到a[n]的数据进行调整，使其满足大顶堆的特性*/
/*a[]是待处理的数组，m是起始坐标， n是终止坐标*/
void heapadjust(int a[], int m, int n) 
{ 
  int i, temp; 
  temp=a[m]; 
  
  for(i=2*m;i<=n;i*=2)//从m的左孩子开始 
  { 
    if(i+1<=n && a[i]<a[i+1])//如果左孩子小于右孩子，则将i++，这样i的值就是最大孩子的下标值 
    { 
      i++; 
    } 
  
    if(a[i]<temp)//如果最大的孩子小于temp，则不做任何操作，退出循环；否则交换a[m]和a[i]的值，将最大值放到a[i]处 
    { 
      break; 
    } 
    a[m]=a[i]; 
    m=i; 
  } 
  a[m]=temp; 
} 
  
void crtheap(int a[], int n)//初始化创建一个大顶堆 
{ 
  int i; 
  for(i=n/2; i>0; i--)//n/2为最后一个双亲节点，依次向前建立大顶堆 
  { 
    heapadjust(a, i, n); 
  } 
} 
  
/*swap()函数的作用是将a[i]和a[j]互换*/
void swap(int a[], int i, int j) 
{ 
  int temp; 
  temp=a[i]; 
  a[i]=a[j]; 
  a[j]=temp; 
  c++; 
} 
  
void heapsort(int a[], int n) 
{ 
  int i; 
  
  crtheap(a, n); 
  for(i=n; i>1; i--) 
  { 
    swap(a, 1, i);//将第一个数，也就是从a[1]到a[i]中的最大的数，放到a[i]的位置 
    heapadjust(a, 1, i-1);//对剩下的a[1]到a[i]，再次进行堆排序，选出最大的值，放到a[1]的位置 
  } 
} 

线性索引

索引就是把一个关键字与它对应的记录相关联的过程。一个索引有若干个索引项构成，每个索引项至少应包括关键字和对应的记录在存储器中的位置等信息。在索引表中的每个索引项对应多条记录，则称为稀疏索引，若每个索引项唯一对应一条记录，则称为稠密索引。索引按照结构可以分为线性索引、树形索引和多级索引。所谓的线性索引就是将索引项集合组织为线性结构，也称为索引表。

稠密索引

稠密索引是指在线性索引表中，将数据集中的每个记录对应一个索引项。并且索引项一定是按照关键码有序的排列。稠密索引的改进的地方在于：它简化了庞大的原数据集，使原本不能装入内存的庞大的数据集，能一次性的装入内存，并且能够在内存中实现关键字码的排序，并且每一个索引项能够指向磁盘中它代表的原数据记录。

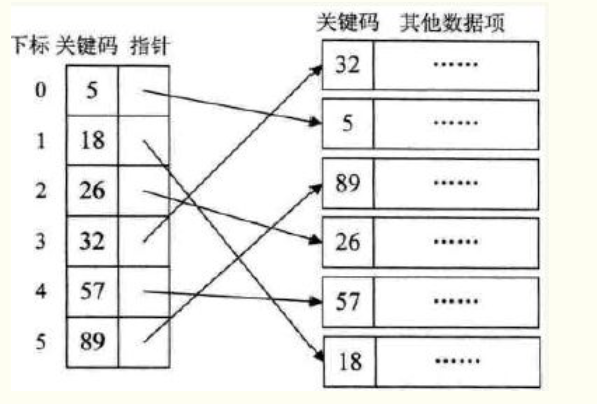
稠密索引是指在线性索引的过程中将数据集中的每个记录对应一个索引项。索引项按关键码有序，索引表是有序表。当索引文件可以在内存中容纳时，将索引文件驻留内存，可用高效查找方法如二分查找实现索引表上的查找，在找到索引项后，可根据其中存放的指向记录的位置信息，可快速找到要找的记录。但若主文件记录数较大，由于是稠密索引，故索引表也会很大，甚至无法存储在内存中，可能就需要反复去访问磁盘，查找性能大大下降。
稠密索引不适合在主文件中进行插入或删除一条记录的运算，因为一旦在文件中插入或删除一条记录，就必然要引起记录的移动。为了使稠密索引文件按关键码有序而且是顺序存储的，索引就必须更新。

• 优点：索引项有序也就意味着，在查找关键字时，可以用到折半、插值、斐波那契等有序的查找算法。
• 缺点：如果数据集非常大，比如说上亿，那也就意味着索引同样的数据规模，可能就需要反复查询内存和硬盘，性能可能反而下降了。

分块索引（稀疏索引）

对于分块有序的数据集，将每块对应一个索引项，这种索引方法叫做分块索引。索引项结构分为三个数据项：最大关键码、块长和块首指针。

分块有序是把数据集的记录分成了若干块，并且这些块需要满足两个条件：

• 块内无序
  每一块内的记录不要求有序
• 块间有序
  比如要求第二块记录的关键字均要大于第一块中所有记录的关键字，第三块要大于第二块。

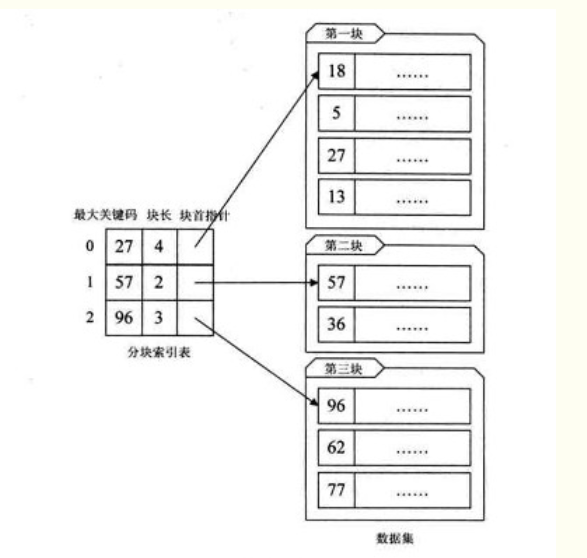
上图中定义的索引项的结构分为三个数据项：

• 最大关键码，它存储了每一块中的最大关键字，这样的好处是可以使得在它之后的下一块中的最小关键字也能比这一块最大的关键字要大。当然这个索引关键字码可以是任何能够唯一标识一个块的任何数据。
• 块长，存储了块中记录的个数，以便于循环时使用。
• 块首地址，用于指向块首数据元素的指针，便于开始对这一块中记录遍历

在分块索引表中查找，可以分为两步：

• 在分块索引表中查找要查的关键字所在块。
  由于分块索引表是块间有序的，因此很容易利用折半插值等算法得到结果。
• 根据块首指针找到相应的块，并在块中顺序查找关键码。
  因为块中可以是无序的，因此只能顺序查找。

#define ILMSize 60;
#define MaxSize 3600；
//建立索引项结构
struct IndexItem
{
    int index;
    int start;
    int length;
};
//建立索引表
typedef struct IndexItem indexList[ILMSize];    //ILMSize为事先定义好的整型常量，大于等于索引项数目m
//建立原始数据的主表
int mainList[MaxSize];  //MaxSize为事先定义好的整型常量，大于等于主表中的记录的个数n
int blockSearch(mainList A, indexList B, int m, int elem)
{
    for(int i = 0; i < m; i++)
        if(B[i].index >= elem)
            break;
    if(i == m)
        return -1;  //查找失败
     
    int endNum = B[i].start + B[i].length;
    for(int j = B[i].start; j < num; j++)
        if(A[j] == elem)
            break;
    if(j < num)
        return j;
    if(j == num)
        return -1;
}

多重表

若不仅要按主关键码进行查找，还要按次关键码按给定码值或给定取值范围进行查找，则需在建立主索引的同时，也建立次关键码索引。

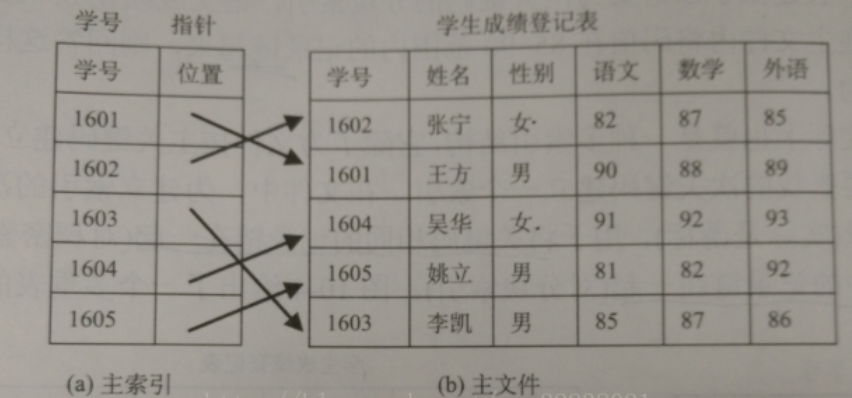
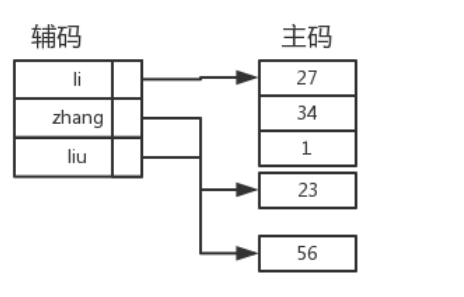
倒排表

由辅码与一个或多个标识号关联起来，标识号索引再关联一个标识号和一个完整记录的指针关联起来，这样组织起来的辅码索引称为倒排表或倒排文件。

• 优点：
  （1）既适合主关键码查找，也适合次关键码的查找
  （2）查找速度较快
  （3）没有要求对主文件中次关键码相同的记录建立链接，因而不需要对主文件进行修改，故其使用和维护简单方便
• 缺点：
  （1）由于记录号表是不定长的，故处理起来不太方便
  （2）由于倒排表的记录号表中记录号要求有序，这对在主文件中进行插入和删除记录操作带来相应处理上的工作量

谈谈你对查找的认识及学习体会。

• 查找：向数据集或数组中发现某一目标值的操作。一共有七大查找算法分别是：顺序查找、树表查找、哈希查找、二分查找、插值查找、斐波那契查找、分块查找。前四种查找算法比较熟悉，后面三种就是了解不是特别熟悉。查找分为两种，一种是静态查找，一种是动态查找。静态查找，就是仅仅作查询和检索的功能，而动态查找则是在静态查找的基础上增添了增加数据和删除数据的功能。通过查找算法的评价指标（ASL），我们能比较各算法的优劣。ASL是指找到（找不到）查找表中记录平均需要的关键字比较次数。线性表的查找中，学习了三种查找方法：顺序查找、二分查找、分块查找。顺序查找就是我们最初的简单算法，将数组遍历一遍查找数据，二分查找则是顺序查找的改进，每一次取中间值进行比较，从效率上看，时间复杂度从顺序查找的O(n)变为了O(log2n)，效率大大提高。分块查找就是将数据分为一个一个的有序块，是一种介于顺序查找和二分查找查找方法。除了线性表，我们这张学习的内容——树表。树表查找的代码比较难写，但是专研还是可以弄懂的。这一章对代码要求不高，但是涉及的内容更广更全面了同时也暴露了前面知识的缺漏，比如对树的掌握对递归的掌握还不扎实。而且查找这章除了要求的代码外更多的是关于平衡树的调整操作，B树的删除增加调整操作等，还有关于各种查找方式对应的查找效率ASL的计算是不同的，要搞清楚这些计算首先得先清楚这些查找的原理然后再记忆其ASL的计算方式才不容易混淆。
• 排序：这周主要学习了五种排序算法，快速排序、希尔排序、直接插入排序、归并排序、堆排序。最简单的肯定是直接插入排序法，希尔排序和归并排序也是比较容易理解，快速排序和堆排序刚开始没有很懂，就在网上看图解，才一步步懂了，看懂之后就很好理解了。我们上个学期学了直接选择排序和冒泡排序，这学期新学习的排序方法可以让我们完善。冒泡排序、直接插入排序、选择排序，这三种排序方法都有循环嵌套，因此它们的时间复杂度较高为O(n^{2)，快速排序、堆排序、归并排序都进行了适当的优化，它们的时间复杂度为O(nlogn)，希尔排序的时间复杂度介于O(n}2)~O(nlogn)两者之间。我个人比较喜欢快速排序，因为它的时间复杂度不高、代码也不复杂。不稳定的排序算法：选择排序、快速排序、堆排序、希尔排序、基数排序。稳定的排序算法：插入排序、冒泡排序、归并排序、二叉树排序、计数排序、 桶排序。

2.PTA题目介绍

2.1 是否完全二叉搜索树

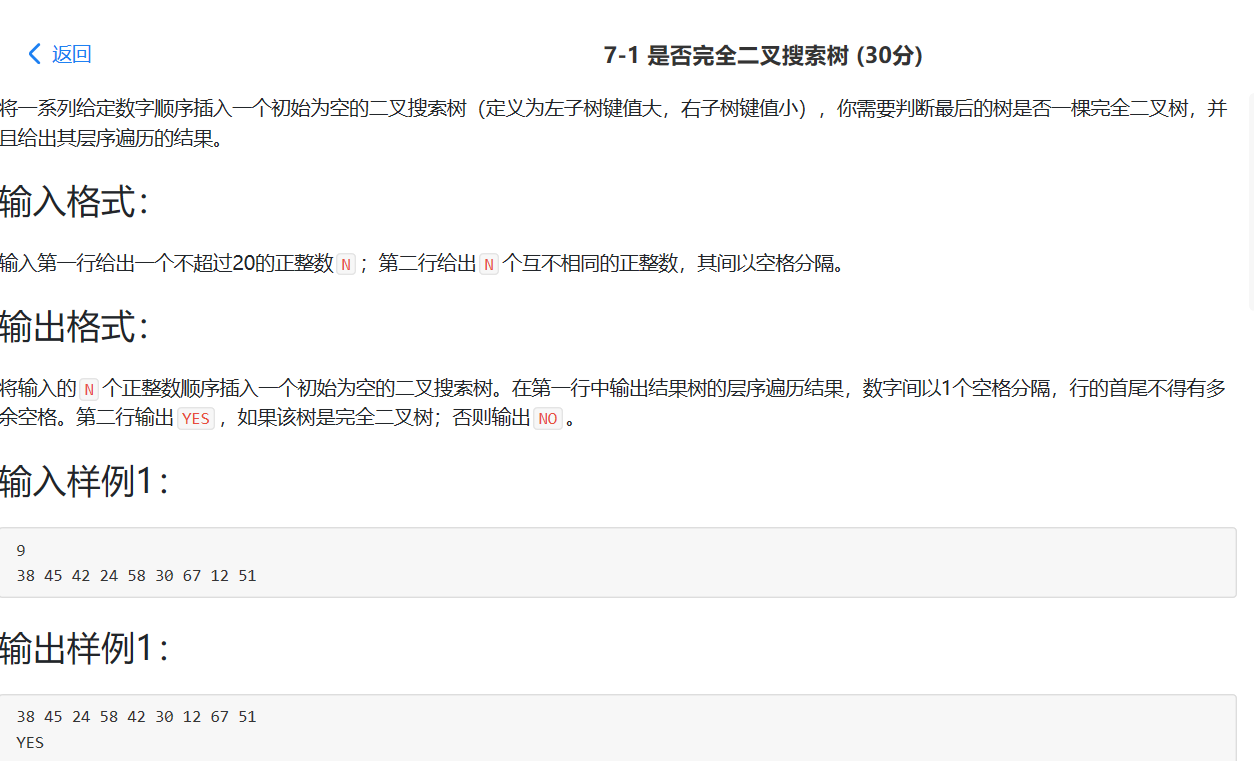
代码

#include<iostream>
using namespace std;
int BST[25] = { 0 }; //用数组构造树结构
int Creat();
void Judge(int max);
int main()
{          
    int max;
    max = Creat();
    Judge( max);
}
int Creat()
{
    int n;
    int index, number;
    int maxindex = 0;

    cin >> n;
    while (n--)
    {
        cin >> number;
        index = 1;
        while (BST[index]) //根据父结点的下标关系，找到要插入的number的位置
        {
            if (number > BST[index])
                index = index * 2;
            else
                index = index * 2 + 1;
        }
        if (index > maxindex)
            maxindex = index;
        BST[index] = number;
    }
    return maxindex;
}
void Judge(int max)
{
    int flag = 1;
    int i;
    for (i = 1; i <= max; i++)
    {
        if (BST[i])
        {
            if (i == 1)
                cout << BST[i];
            else
                cout << " " << BST[i];
        }
        else
            flag = 0;
    }
    cout << endl;
    if (flag == 1)
        cout << "YES" << endl;
    else
        cout << "NO" << endl;
}

2.1.1 该题的设计思路

创建二叉搜索树： 满足二叉搜索树的条件（定义为左子树键值大，右子树键值小），将输入的number通过下标关系利用循环插入到正确的位置，并且保留该二叉搜索树的最大下标max以便判断是否为完全二叉搜索树。

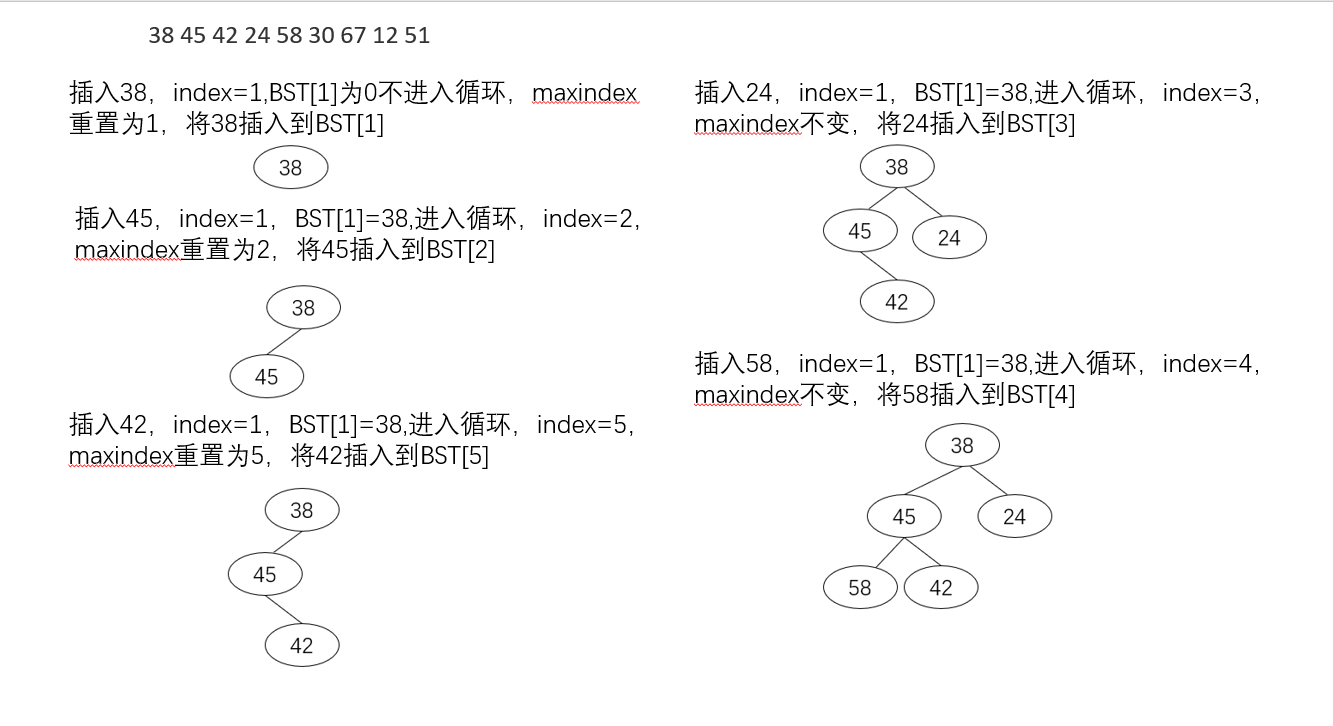
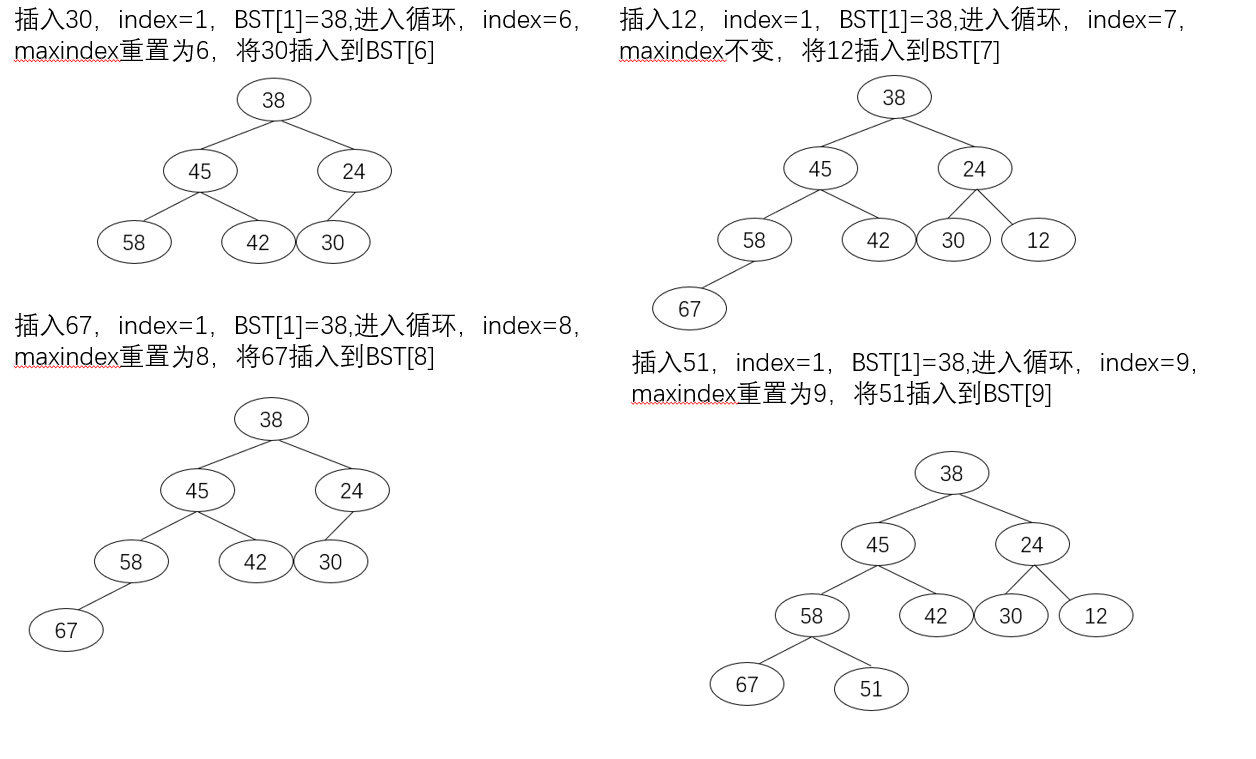
判断完全二叉树： 根结点的下标从1开始计数，从上到下、从左到右给每个结点编号，则到最大下标数为止，结点都不能为空才满足完全二叉树的定义，否则就不是完全二叉树。

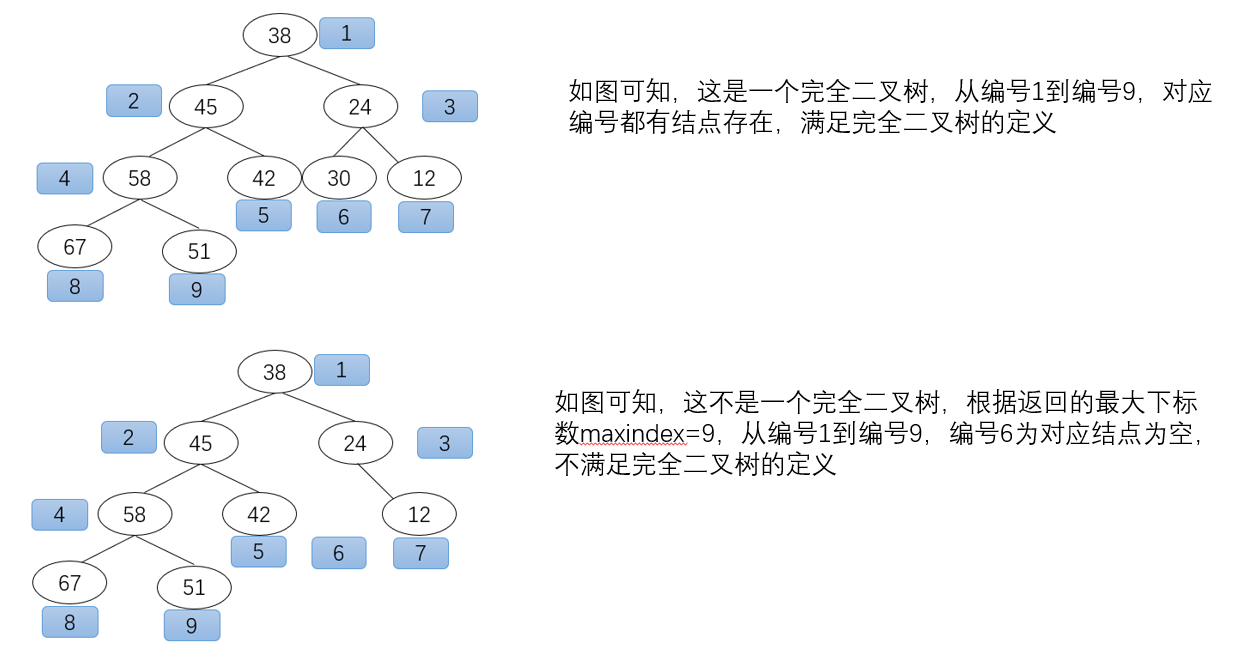
时间复杂度为O(nlogn)

2.1.2 该题的伪代码

定义BST[25]={ 0 }用数组代替树结构
int Creat()函数
{
      定义index来记录下标，maxindex = 0记录所创二叉树最远叶子节点的下标
      输入结点个数n
      while(n--)
            输入结点关键字number
            数组下标index初始化为1
            while(BST[number]不为空) //找到number要插入的位置
                  if(number大于BST[index])
                        index重新赋值为2*index
                  else
                        index重新赋值为2*index+1
                  end if
            end
      if(index大于maxindex)
            maxindex重新赋值为index
      end if
      把number插入到下标为index的位置
      return maxindex                                   
}
void Judge(int max)函数
{
      定义flag=1判断是否为完全二叉搜索树
      for int i=1 to max do i++
            if(BST[i]不为0)
                  输出BST[i]
            else
                  flag=0
            end if
      end for
      输出换行
      if(flag为1)
            输出“YES”
      else
            输出“NO”
      end if
}
int main()函数
{
      定义max储存题目输入的二叉树所能到达的最大叶子结点下标
      
      max=Creat()
      Judge(max)
}

2.1.3 PTA提交列表

Q1：提交的时候发现是段错误问题，就去找死循环问题了
A1：刚开始找的时候没找到，觉得while(BST[index])循环不会死循环就去Creat函数里面看遍历的问题发现也不是，之后才找到是我建树的问题，将输入的number插入的时候要经过一个循环找到位置，这个循环是要从根结点开始找插入的位置，所以index在进入这个循环的时候都要从1开始，所以要加入这条语句

Q2：提交还是答案错误，就继续找问题了
A2：Judge函数里面，刚开始设置的遍历终点是输入结点个数n。如果输入的不是完全二叉搜索树而且是最大的结点的话那这个遍历就会出问题，所以我在Creat函数里面增加了一个maxindex储存输入结点的最大下标数，每有一次插入就重置最大下标。

Q3：部分正确那边我也不是很清楚，觉得自己好像没错，就去问了助教
A3：原来是我的Judge函数的问题，我之前以为完全二叉树是每个结点都要有两个孩子，但其实只用最后一层是结点从左到右是连续的，其他的是每个结点要有两个孩子，所有Judge函数的遍历从1到maxindex每个结点都存在即可，为空就不满足。

2.1.4 本题设计的知识点

• 二叉搜索树的创建： 利用左子树的位置为2×i、右子树的位置为2×i+1的下标关系用数组代替树结构，通过while()循环找到输入数字该插入的位置。熟悉了二叉搜索树的结构也熟悉了建树的操作。树的基本操作都是要烂熟于心的，这道题目能加强记忆。
• 理解完全二叉树： 一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，编号为i的结点与满二叉树中编号为i的结点在二叉树中的位置相同。区别了完全二叉树和满二叉树，理解它的概念之后这道题目就会简单很多就是直接判断该有元素的位置有没有元素就行了。
• 二叉树的层次遍历： 如果用链表建树，层次遍历就需要用到辅助队列来存储结点元素，但是我写这道题目的时候耍了小聪明用的数组，相当一部分的简化了代码，元素插入的过程模拟了二叉树，数组的顺序遍历就是二叉树的层次遍历了。

2.2 题目2

代码

#include<iostream>
#include<map>
#define MAXV 32767
using namespace std;
typedef struct TNode
{
	int data;
	TNode* left;
	TNode* Right;
}*BST;
BST CreatTree(int left, int right, int number[]);
int IsSon(BST tree, int num);
int IsFather(BST tree, int U, int V);
BST IsLCA(BST tree, int U,int V);

int main()
{
	int number[MAXV], count[MAXV] = { 0 }; //count数组用来计算下标是否是树结点
	int M, N, U, V;
	int i, j;
	BST tree, temp;
	map<int, int> mp;

	tree = NULL;
	cin >> M >> N;
	for (i = 1; i <= N; i++)
	{
		scanf("%d", &number[i]);
		mp[number[i]]++;
	}
	tree = CreatTree(1, N, number);
	
	for (i = 1; i <= M; i++)
	{
		cin >> U >> V;
		/*if (count[U] == 0 && count[V] == 0)
			cout << "ERROR: " << U << " and " << V << " are not found." << endl;
		else if (U < 0 && V < 0)
			cout << "ERROR: " << U << " and " << V << " are not found." << endl;
		else if (count[U] == 0 && V < 0)
			cout << "ERROR: " << U << " and " << V << " are not found." << endl;
		else if (count[V] == 0 && U < 0)
			cout << "ERROR: " << U << " and " << V << " are not found." << endl;
		else if ((count[U] == 0 && count[V] != 0) || (U < 0 && count[V] != 0))
			cout << "ERROR: " << U << " is not found." << endl;
		else if ((count[V] == 0 && count[U] != 0) || (V < 0 && count[U] != 0))
			cout << "ERROR: " << V << " is not found." << endl;*/
		
		if (mp[U] == 0 && mp[V] == 0)
			cout << "ERROR: " << U << " and " << V << " are not found." << endl;
		else if (mp[U] == 0)
			cout << "ERROR: " << U << " is not found." << endl;
		else if (mp[V] == 0)
			cout << "ERROR: " << V << " is not found." << endl;
		else
		{
			int num1, num2;

			num1 = IsFather(tree, U, V);
			num2 = IsFather(tree, V, U);
			if(num1==1)
				cout << U << " is an ancestor of " << V << "." << endl;
			else if(num2==1)
				cout << V << " is an ancestor of " << U << "." << endl;
			else
			{			
				temp = IsLCA(tree, U, V);
				cout << "LCA of " << U << " and " << V << " " << "is" << " " << temp->data << "." << endl;
			}
		}
	}

	return 0;
}
BST CreatTree(int left, int right, int number[])
{
	if (left > right) //不满足二叉搜索树的定义
		return NULL;
	BST node;
	int i;

	node = new TNode;
	node->data = number[left];
	node->left = node->Right = NULL;

	for (i = left + 1; i <= right; i++)//找到第一个大于根结点的数去建右子树
		if (number[i] >= number[left])
			break;

	node->left = CreatTree(left + 1, i - 1, number);
	node->Right = CreatTree(i, right, number);
	return node;
}
int IsSon(BST tree, int num)
{
	if (tree != NULL)
	{
		if (tree->data == num)
			return 1;
		else if (num < tree->data)
			return IsSon(tree->left, num);
		else
			return IsSon(tree->Right, num);
	}
	return 0;
}
int IsFather(BST tree, int U, int V)
{
	if (tree != NULL)
	{
		if (tree->data == U)
		{
			if (IsSon(tree, V) == 1)
				return 1;
			else
				return 0;
		}
		else if (U < tree->data)
			return IsFather(tree->left, U, V);
		else
			return IsFather(tree->Right, U, V);
	}
	return 0;
}
BST IsLCA(BST tree, int U, int V)
{
	if (tree->data > U&& tree->data > V)
		return IsLCA(tree->left, U, V);
	else if (tree->data < U && tree->data < V)
		return IsLCA(tree->Right, U, V);
	else
		return tree;
}

2.2.1 该题的设计思路

创建二叉搜索树： 根据输入的元素，找到第一个大于根结点的元素，保留该元素的下标，通过递归创建根结点的左子树和右子树。就可以根据题目输入的先序序列创建二叉搜索树。

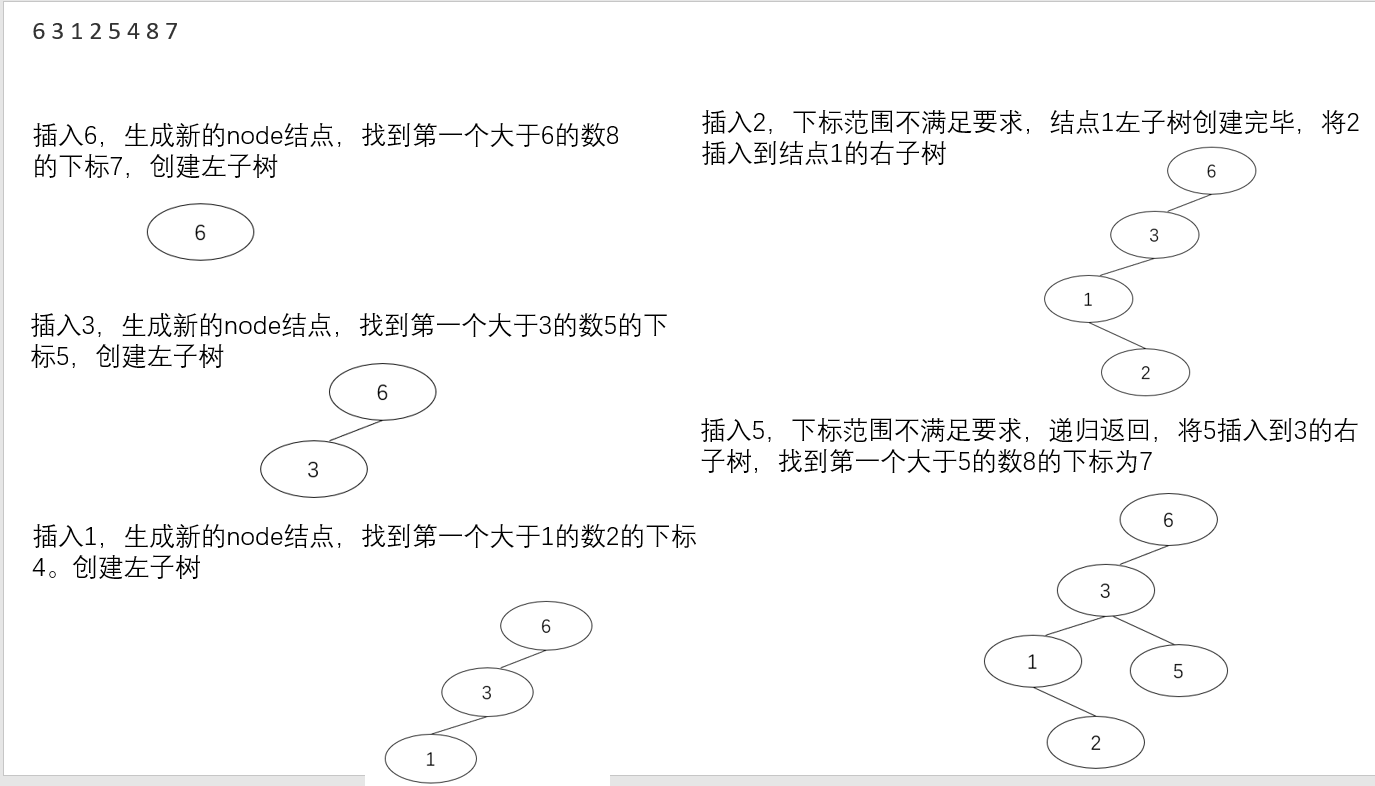
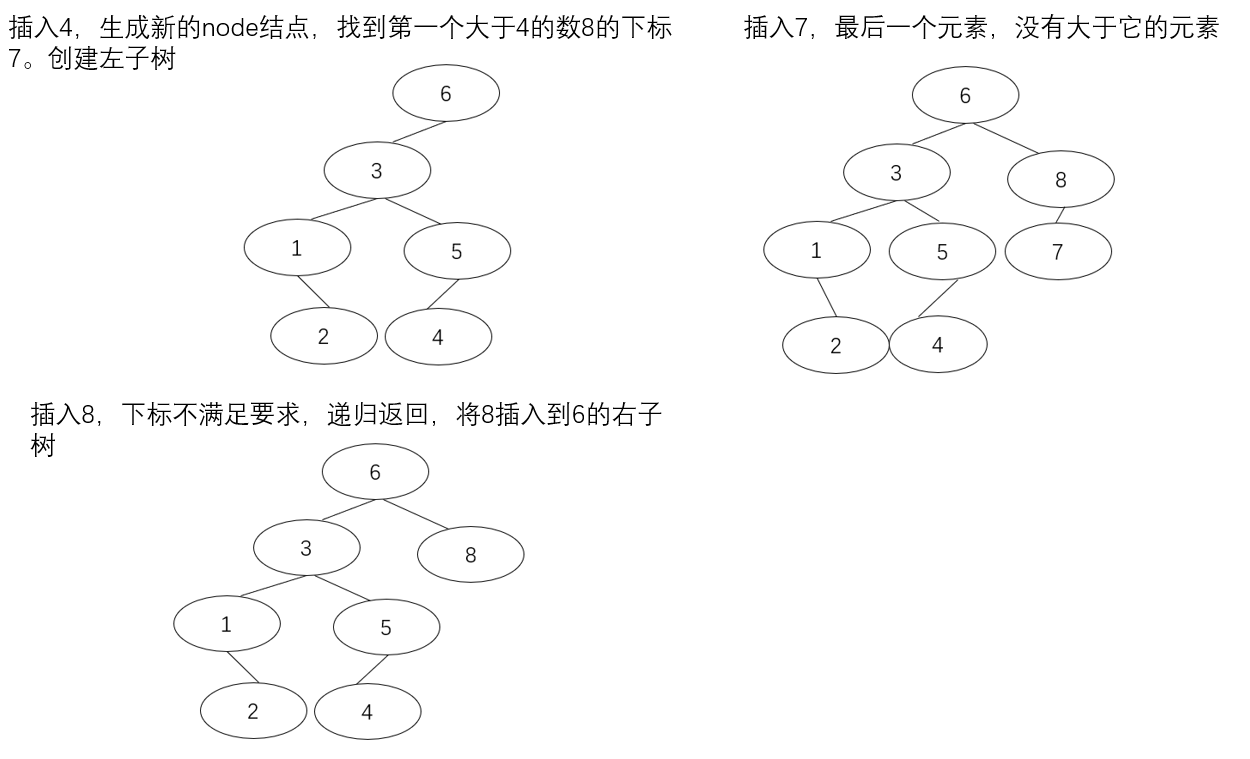
判断U、V关系： 从根结点开始，查找有没有结点元素等于U，如果有结点元素等于U，则查找该结点的子树中是否存在结点元素等于V，如果存在U、V关系，则说明U、V存在父子关系；如果U、V不存在父子关系，那么就查找它们的最近公共祖先，从根结点开始，判断结点元素与U、V的大小，如果U、V都小于根结点元素，递归到根结点的左子树查找祖先，如果U、V都大于根结点元素，递归到根结点的右子树查找祖先，如果U、V一个大于结点元素一个小于结点元素，那么这个结点元素就是它们两个的最先公共祖先

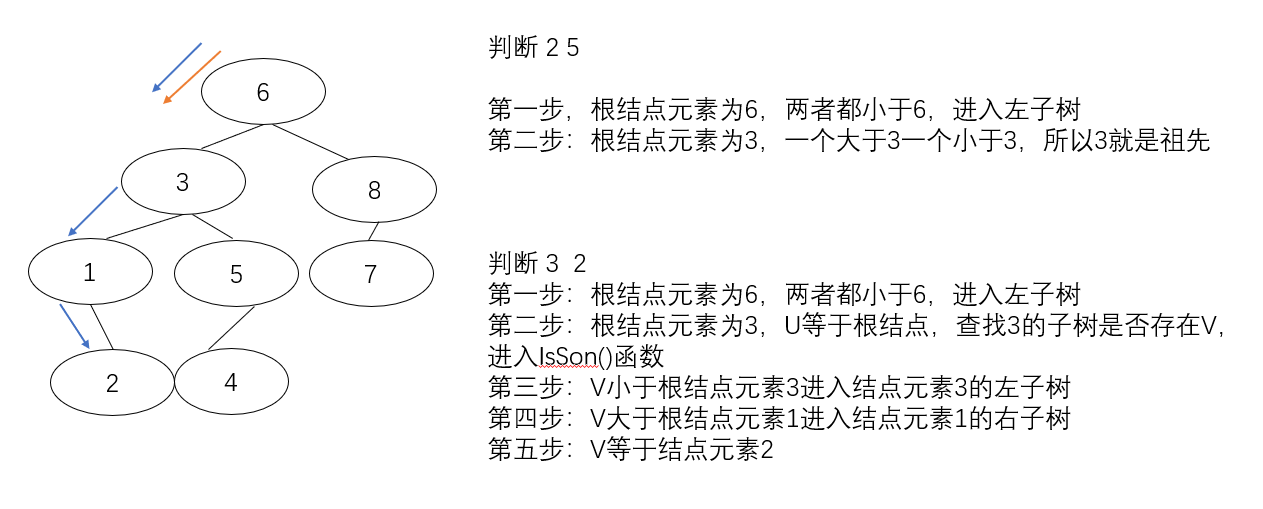
时间复杂度O(nlogn)

2.2.2 该题的伪代码

树结点结构：
typedef struct TNode
{
	int data;
	TNode* left;
	TNode* Right;
}*BST;
BST CreatTree(int left, int right, int number[])函数
{
      if(lefe大于right) //不满足树的定义
            return NULL
      end if
      
      生成新结点node，node->data存放number[left]，node左右结点置为NULL
      
      for int i =left+1 to right do i++ 
            if(number[i] 大于 number[left]) //找到第一个大于根结点的元素建右子树
                  break
            end if
      end
      //利用递归去创建node的左右子树
      node->left = CreatTree(left + 1, i - 1, number)
      node->Right = CreatTree(i, right, number)
      return node
}
int IsFather(BST tree, int U, int V)函数
{
      if(tree不为空)
            if(tree->data 等于 U)
                  if(IsSon(tree,V)为真)
                        return 1
                  else
                        return 0
                  end if
            else if(U 小于 tree->data)
                  return IsFather(tree->left, U, V)
            else
                  return IsFather(tree->Right, U, V)
            end if
      end if
      return 0;
}
int IsSon(BST tree, int num)函数
{
      if (tree 不为空 )

            if (tree->data 等于 num)
                  return 1
            else if (num 小于 tree->data)
                  return IsSon(tree->left, num)
            else
                  return IsSon(tree->Right, num)
            end if
      end if
     return 0;
}
BST IsLCA(BST tree, int U, int V)函数
{
	if ( U、V都小于 tree->data )
		return IsLCA(tree->left, U, V);
	else if (U、V都大于 tree->data)
		return IsLCA(tree->Right, U, V);
	else
		return tree
}
int main()函数
{
      定义number[]数组存放先序输入的元素
      定义tree创建二叉搜索树
      定义mp存放输入结点判断查询元素是否存在
      输入M，N
      for int i=1 to N do i++
            输入元素存放到number[i]
            mp[number[i]]++
      end 
      tree = CreatTree(1, N, number)
      
      for int i=1 to M do i++
            输入U，V
       
      if (mp[U] 、mp[V] 都为0)
            输出
      else if(mp[U] 等于 0)    
            输出
       else if(mp[V] 等于 0)    
            输出
      else
            //判断U、V是否存在父子关系
            int num1=IsFather(tree, U, V)
            int num2=IsFather(tree, V, U)
            if(num1)
                  输出
            else if(num2)
                  输出
            else
                  定义树结构的temp=IsLCA(tree,U,V)
                  输出
            end if
      end if
}

2.2.3 PTA提交列表

Q1：部分正确，VS运行的时候，如果输入的是负数，这个负数不会输出找不到
A1:判断输入的结点是否存在的时候我用了很多个if-else-if判断。改了之后发现运行的时候负数会输出找不到了。

Q2：建树那个地方出现了问题，不知道是死循坏还是什么就卡着不能结束运行
A2:递归建树的时候，建树的传参出现了问题。左子树传参应该是(left+1,i-1,number) 、右子树传参应该是(i,right,number)，但是我之前的代码左子树传参是(left,i,number) 、右子树传参是(i+1,right,number)。所以这个建树出现了错误。
Q3：U、V是否存在父子关系这里我写的代码有点错乱，运行输出有的时候是反的，有的时候又不是反的。
A3:我就定义了两个函数，来判断U、V是否存在父子关系。如果某个结点的元素等于U，去寻找U的子树元素是否存在V，如果满足条件就是存在父子关系。

Q4：查找共同最先祖先的敌法卡了一下，没想到法子去找.....
A4:然后想了想，利用二叉搜索树的性质，左子树的结点的值都小于根结点的值，右子树的结点的值都大于根结点的值，判断给出的俩个值是不是一个大于一个小于，如果是则这时的根结点就是我们要找的
Q5：还有一分不知道卡在哪里，一直不能过
A5：然后我去问老师，老师说我输入负数的时候，还要用负数当个数组的下标去判断是否存在该元素，让我改用map容器来做。

2.2.4 本题设计的知识点

• 先序序列创建二叉树： 建立二叉搜索树的过程就是根据其定义找到第一个大于根结点元素的下标index，由下标left+1index-1创建根结点的左子树，下标indexright创建根结点的左子树，利用递归完成整个树的创建过程。我这样写复杂了代码，也增加了代码运行的时间复杂度，老师说其实先序遍历树结点序列可以直接插入树中，因为先序遍历的过程和建树的过程是一样的，所以建树过程变得简单好理解。理解之后反应我当时怎么就没想到呐太笨了。
• map映射待测结点是否存在树中： 我之前本来是用一个数组来存放加入过的树结点元素，将元素作为数组的下标count[number[i]]自增，这样写之后因为有负数的存在对待测U、V的判断就会很复杂，要将U、V负数情况分开讨论，条件判断里面又有条件，代码看着都难受一点都不精简。引用map的映射之后直接四行代码解决问题。不得不说STL容器是真的很厉害，作用太多了。
• 待测U、V问题解决： 如果是父子关系，那么其中有一个元素与树结点元素相等，另一个就存在在结点元素的子树中；如果不是父子关系，U、V一个大于根结点，一个小于根结点元素，这个根结点元素就是LCA。

2.3 (哈希链) 航空公司VIP客户查询

代码

#include<iostream>
#include<string.h>
#define MAX 100007
using namespace std;

typedef struct HashNode
{
	char id[19];
	int len;
	struct HashNode* next;
}HashNode, * HashTable;
void Insert(HashTable ht[], char num[], int id, int len);
int GetHashId(char num[]);
int Find(HashTable ht[], char num[]);
int main()
{
	int N, K, lenth, M;
	char num[19];
	HashTable ht[MAX];
	int i, j;

	for (i = 0; i < MAX; i++)
	{
		ht[i] = new HashNode;
		ht[i]->len = 0;
		ht[i]->next = NULL;
	}
	scanf("%d%d", &N, &K);
	while (N--)
	{
		scanf("%s%d", num, &lenth);
		if (lenth < K)
			lenth = K;
		int id;
		id = GetHashId(num);
		Insert(ht, num, id, lenth);
	}

	scanf("%d", &M);
	while (M--)
	{
		scanf("%s", num);
		int no;
		no = Find(ht, num);
		if (no == -1)
			printf("No Info\n");
		else
			printf("%d\n", no);
	}

	return 0;
}
int GetHashId(char num[])
{
	int len = 0;

	for (int i = 13; i < 17; i++)
		len = len * 10 + (num[i] - '0');
	if (num[17] == 'x')
		len = len * 10 + 10;
	else
		len = len * 10 + (num[17] - '0');
	len = len % 100007;
	return len;
}
int Find(HashTable ht[], char num[])
{
	int id;
	HashTable node;

	id = GetHashId(num);
	node = ht[id]->next;
	while (node != NULL)
	{
		if (strcmp(node->id, num) == 0)
			return node->len;
		node = node->next;
	}
	return -1;
}
void Insert(HashTable ht[], char num[], int id, int len)
{
	HashTable node, temp;
	int flag = 1;

	temp = ht[id]->next;
	while (temp != NULL)
	{
		if (strcmp(temp->id, num) == 0)
		{
			temp->len += len;
			flag = 0;
			return;
		}
		temp = temp->next;
	}
	temp = ht[id];
	if (flag == 1)
	{
		node = new HashNode;
		node->len = len;
		strcpy(node->id, num);
		node->next = NULL;
		node->next = temp->next;
		temp->next = node;
	}
}

2.3.1 该题的设计思路

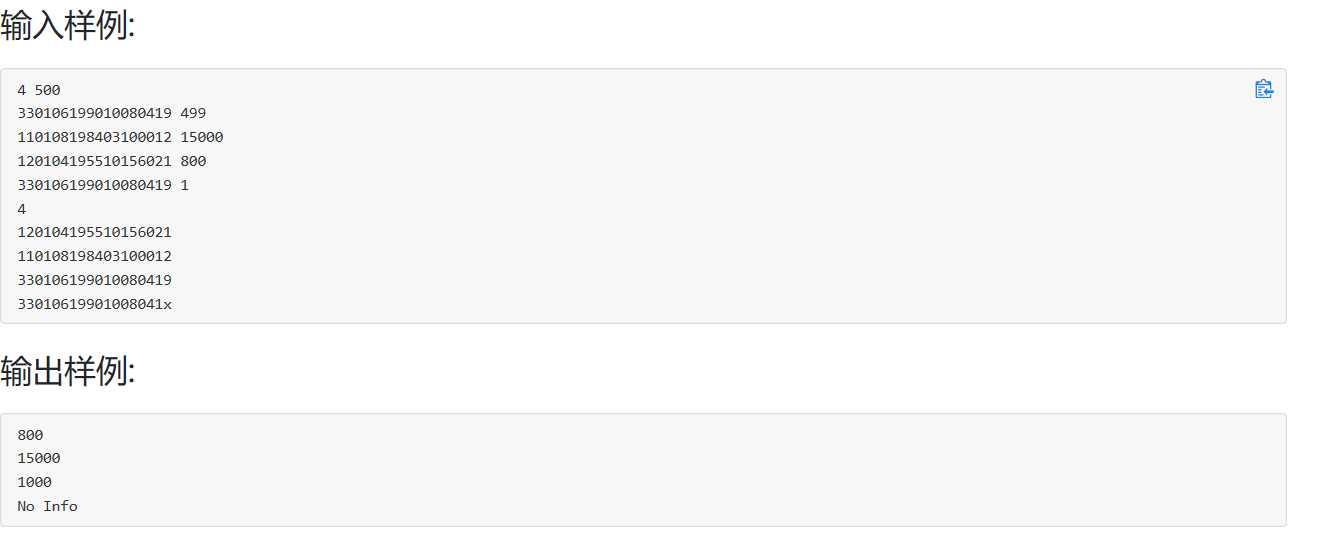
创建哈希链： 根据用户输入的身份证号找到其哈希地址，创建一条哈希链，将身份证存到结点id中，将里程放入到len中，如果哈希地址相同，比较该地址上的链中是否有与新插入结点相同的id，没有就直接头插法插入即可，有的话将飞行里程相加即可。

合理的获取哈希地址： 身份证高达18位，如果每一位数都要取的话，时间复杂度会高很多，身份证后四位是证明号码在加上前面一位出生日期就很少会出现地址冲突，取身份证后五位采用除留余数法获取哈希地址。

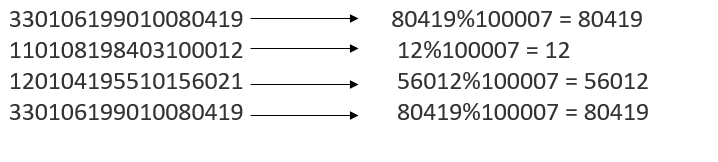
时间复杂度O(n)

2.3.2 该题的伪代码

链表结构体：
typedef struct HashNode
{
	char id[19];
	int len;
	struct HashNode* next;
}HashNode, * HashTable;
int GetHashId(char num[])
{
      定义len=0存放id的后五位数字
      for int i=13 to 17 do i++
            获取身份证13到16的四位数存放到len中
      对身份证最后一位进行判断，如果最后一位是‘X’，就加10，如果不是就加最后一位这个数
      len=len%100007
      return len      
}
void Insert(HashTable ht[], char num[], int id, int len)函数
{
      定义flag=1用来判断加入结点是否在链表中存在
      定义树结构temp=ht[id]->next
      while(temp不为空)
            if(temp->id和num是一样的身份证号)
                  temp结点的飞行里程叠加，temp->len+=le
                  flag=0
                  return
            end if
            temp=temp->next
      end
      temp = ht[id]
      if(flag==1)
            生成新结点，利用头插法将新生成的结点插入到哈希地址链中
      end if                  
}
int Find(HashTable ht[], char num[])
{
      定义id=GetHashId(num)
      定义树结构node=ht[id]->next
      while(node不为空)
            if(node->id和num是一样的身份证)
                  return node->len
            end if
            node=node->next
      end 
      return -1            
}
int main()函数
{
      定义树结构数组ht[MAX]
      for int i=0 to MAX do i++
            给每一条ht[i]申请空间，ht[i]->next=NULL,ht[i]->len=0
      end 
      输入N，K
      while(N--)
            输入身份证num和飞行里程lenth
            将lenth不足最低里程K的置为K
            int id=GetHashId(num)
            Insert(ht, num, id, lenth)
      end 
      输入M
      while(M--)
            输入身份证num
            int no = Find(ht, num)
            if(no等于-1)
                  输出
            else
                  输出
            end if
      end
}

2.3.3 PTA提交列表

Q1:当时输出的和样例不一样，输入的第三个身份证输出的飞行里程是500，但是样例是1000就不知道怎么回事了
A1:然后去问了一下同学为什么输出的是1000，她说题目有规定说不满最低里程K的都按K来算。

Q2:我刚开始的哈希链不是将相同地址的建在一条链上，而是只将同一个身份证号的建立在同一条链上，ht[id]->len存放总的飞行里程
A2:但是想想这样的话，如果是结点数达到最大值，哈希地址大概率会不够，所以我就修改了建链的代码，这样也才是哈希链的正确建立方式，我之前那种建链方式严格上说根本就不满足哈希链的定义，哈希链是不会有数据溢出或者说是堆积的，所以修改之后的建链方式是比较OK的，如果身份证是相同的哈希地址，就遍历该地址对应的哈希链，如果有身份证号是一样的就修改飞行里程，如果遍历到底都没有一样的身份证号就生成一个新结点利用头插法将新结点插入链中。

Q3:提交之后过不去的测试点都显示的是段错误或者运行超时就去优化自己的代码了
A3:我之前获取哈希地址本来是将整个18号身份证进行处理然后利用除留余数法获取哈希地址，但是对每个18位身份证进行处理也要很久，就去和同学讨论地址的获取方法，助教也说其实可以不用将全部的身份证号进行处理，可以只将后五位进行处理就好，这样可以优化代码降低代码运行时间。

Q4:前面讲身份证号码数优化之后还是会运行超时，真的不知道什么问题
A4:问了过了的同学，也让她们帮我看了一下代码，除了输出那个地方的不同也没啥了，我就去问了林老师，老师说这道题目输入输出要用scanf 、printf，相比cin、cout来讲，前者的运行时间会更短一点，之后我又去百度了为什么cin、cout运行时间会更长，影响cout和cin的性能的有两个方面：同步性和缓冲区，同步性可以通过 ios_base::sync_with_stdio(false)禁用；操作系统会对缓冲区进行管理和优化，但十分有限，还有一个cout和cin的绑定效果，两者同时使用的话，cin与cout交替操作，会有一个flush过程，所以还是会很漫长。
Q5:我把前面身份证数、输入输出的问题都更改了之后提交还是运行超时，差点吐出一口老血，太困难了
A5:没有办法了，我只能一步一步的去看我的代码，终于的终于我发现了问题，我更是一口老血都想锤死我自己了，我在查找函数里面对于定地址的哈希链遍历的时候，没有写循环条件。这真的是细节决定成败了，我经常会犯这种小错误，从小到大的马大哈，一定要记得这些细节啊，要注重细节。

2.3.4 本题设计的知识点

• 建立哈希链： 本题要求我们用哈希链去做，所以可以熟悉哈希链的操作以及正确建立哈希链的过程，了解哈希链的正确建立过程也就可以清楚为什么使用哈希链不会造成数据堆积问题。同时也熟悉了链表的操作，插入结点那一块我们使用的是头插法。数据结构对链表的要求很高，大部分的题目都是使用链表来完成，所以链表的基本操作我们不可以忘记更是要熟练了。
• 解决地址冲突： 使用拉链法建立哈希表，很轻松的解决了哈希冲突的问题，不会担心哈希地址不够、数据溢出等问题。利用除留余数法获取哈希地址，余数设立合理，这样也很大一部分解决地址冲突问题。如果这道题目使用map容器映射来写，就不会这样麻烦，不会用地址冲突的问题。
• cin、cout和scanf、printf运行时长不同： cout和cin速度比printf和scanf慢一个数量级以上。cin，cout之所以效率低，是因为先把要输出的东西存入缓冲区，再输出，导致效率降低。使用ios::sync_with_stdio(false)语句可以打消iostream的输入输出缓存，可以节省许多时间，使效率与scanf与printf相差无几，但是还是比scanf与printf略慢。