DS博客作业03--树
0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
串的BF\KMP算法
| BF算法 |
BF算法思想
1.在串 S 和串 T 中分别设比较的起始下标 i 和 j;
2.循环直到 S 中所剩字符个数小于 T 的长度或 T 的所有字符均比较完,如果 S[i]=T[j] ,则继续比较S和T的下一个字符;如果S[i]!=T[j],将i和j回溯,准备下一趟比较;
3.如果 T 中所有字符均比较完 , 则匹配成功 , 返回匹配的起始比较下标 ; 否则 ,匹配失败 ,返回 0;
BF算法代码
int BF(char[] s, char[] p)
{
int i = 0;
int j = 0;
while(i < s.length && j < p.length)
{
if (s[i] == p[j])
{
i++;
j++;
}
else
{
i = i-j+1;
j = 0;
}
if (j > p.length-1)
return i-p.length;
}
return -1;
}
BF算法执行过程
例:S =″ababcabcacbab″
T =″abc″

BF算法:时间复杂度最好是O(n+m),最差为O(n*m)
| KMP算法 |
KMP算法思想
1.在串 S 和串 T 中分别设比较的起始下标 i 和 j;
2.循环直到 S 中所剩字符长度小于 T 的长度或 T 中所有字符均比较完毕,如果 S[i] = T [j],则继续比较 S 和 T 的下一个字符 ; 如果S[i] != T [j],将 j 向右滑动到 next[ j] 位置 ,即 j = next[j] ; 如果 j = 0 ,则将 i 和 j 分别加 1 ,准备下一趟比较;
3.如果 T 中所有字符均比较完毕 , 则返回匹配的起始下标 ,否则返回 0;
next[]数组计算方法
在“aba”中,前缀是真前缀的所有子串的集合,包括“a”、“ab”,除去最后一个字符的剩余字符串叫做真前缀在“aba”中,真前缀“ab”。同理,真后缀就是除去第一个字符的后面全部的字符串。
next就是前缀和后缀中相同的子串的最大长度
例如:
1. 在“aba”中,前缀是“a”,后缀是“a”,那么两者相同子串最长的就是“a”,相同的子串的最的长度就是1;
2. 在“ababa”中,前缀是“aba”,后缀是“aba”,二者相同子串最长的是“aba”,相同的子串的最的长度就是3;
3. 在“abcabcdabc”中,前缀是“abc”,后缀是“abc”,二者相同子串最长的是“abc”,相同的子串的最的长度就是3;
(这里有一点要注意,前缀必须要从头开始算,后缀要从最后一个数开始算,中间截一段相同字符串是不行的)
得到next[]数组的代码
void getNext(String T, int next[])
{
int i;//循环变量
int k;
next[0] = -1;
for (i = 1; T.str[i] != '\0'; ++i)
{
k = next[i - 1];
while (k != -1)
{
if (T.str[i - 1] == T.str[k])
{
next[i] = k + 1;
break;
}
else
k = next[k];
}
if (k == -1)
next[i] = 0;
}
}
KMP算法代码
int KMP(char[] s, char[] p, int[] next)
{
int i = 0;
int j = 0;
while(i < s.length && j < p.length)
{
if(j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
j = next[j];
}
if(j >= p.lengt)
return i-p.length;
return -1;
}
KMP算法执行过程
例:S =″ababcabcacbab″
T =″abcac″

KMP算法:时间复杂度O(n+m)
| 改进的KMP算法 |
得到nextval[]数组的代码
void get_nextval(int nextval[])
{
Slen=strlen(S)-1;
Tlen=strlen(T)-1;
int i=1,j=0;
nextval[1]=0;
while(i<=Tlen)
{
if(j==0||T[i]==T[j])
{
if(T[++i]!=T[++j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}
else
j=nextval[j];
}
}
二叉树(普通二叉树、完全二叉树、满二叉树、二叉排序树)的定义和性质
二叉树:二叉树是每个结点最多有两个子树的有序树。
任何树可以和二叉树相互转换
二叉树不是树的特殊情况:
- 二叉树可以是空集合
- 根可以有空的左子树或者空的右子树
- 二叉树结点的子树要区分左子树和右子树
性质
性质1:二叉树第i层上的结点数目最多为2i-1(i≥1)。
性质2:深度为k的二叉树至多有2k-1个结点(k≥1)。
性质3:在任意-棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则no=n2+1。
完全二叉树
完全二叉树:若一棵二叉树至多只有最下面的两层上结点的度数可以小于2,并且最下一层上的结点都集中在该层最左边的若干位置上,则此二叉树称为完全二叉树。
特点:
(1) 满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
(2) 在满二叉树的最下一层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
(3) 在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
性质:对完全二叉树中编号为i的结点(n为结点数),有:
(1)若i<(n/2)(下取整),则编号为i的节点为分支节点,否则为叶子节点。
(2)若n为奇数,则每个分支节点都既有左孩子结点,也有右孩子结点。
(3)若编号为i的节点有左孩子结点,则左孩子结点的编号为2i;若编号为i的节点有右孩子结点,则左孩子结点的编号为2i+1。
(4)除树根结点外,若一个节点的编号为i,则它的双亲结点编号为(i/2)(下取整)
(5)具有n个结点的完全二叉树的深度为log2n+1。
满二叉树
满二叉树:一棵深度为k且有2k-1个结点的二又树称为满二叉树。
特点:
(1) 每一层上的结点数都达到最大值。即对给定的高度,它是具有最多结点数的二叉树。
(2) 满二叉树中不存在度数为1的结点,每个分支结点均有两棵高度相同的子树,且树叶都在最下一层上。
二叉排序树
一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
(4)没有键值相等的结点。
二叉树存储结构、建法、遍历及应用
二叉树的储存结构
顺序存储结构
用一组地址连续的存储单元来存放二叉树的元素。对于完全二叉树来说,顺序存储十分合适,能从分利用存储空间,但是对于一般二叉树而言,顺序存储使二叉树的插入删除等操作十分不方便。
typedef struct
{
int data[MAXSIZE];//存放二叉树的节点值
int n;//元素个数
}BTree;
在二叉树中,按从上到下、从左到右的顺序对所有节点由1开始编号,再根据编号存入相应的下标中。对于一般二叉树,将其每个结点编号与满二叉树对应进行储存,这种储存方式会造成大量内存空间的浪费
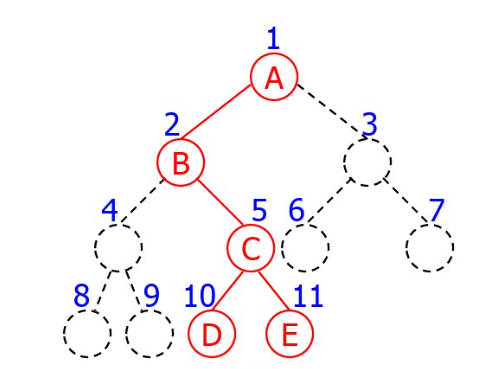
若已知某节点的编号为n,则其左子树的结点编号为2n,右子树的结点编号为2n+1,父结点编号为n/2。
链式存储结构
用一个链表来存一颗二叉树,不会造成存储空间溢出,不会浪费空间
typedef struct node
{
int data;//数据元素
struct node *lchild;//指向左孩子
struct node *rchild;//指向右孩子
}BTree;
二叉树的创建
顺序存储创建
BTree Creat(BTree &bt,char str[], int i)
{
BTree bt;
if (i > strlen(str))
return NULL;
if (str[i] == '#')
return NULL;
bt = new Node;
bt->data = str[i];
bt->lchild = Creat(bt,str, 2*i);
bt->rchild = Creat(bt,str, 2*i+1);
return bt;
}
链式存储创建
BTree Creat(char str[], int &i)
{
BTree bt;
if (i > strlen(str))
return NULL;
if (str[i] == '#')
return NULL;
bt = new Node;
bt->data = str[i];
bt->lchild = Creat(str, ++i);
bt->rchild = Creat(str, ++i);
return bt;
}
二叉树的遍历
先序遍历
void PreOrderTraverse(BiTree T)
{
if(T!=NULL)
{
printf("%c",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
中序遍历
void InOrderTraverse(BiTree T)
{
if(T!=NULL)
{
PreOrderTraverse(T->lchild);
printf("%c",T->data);
PreOrderTraverse(T->rchild);
}
}
后序遍历
void PostOrderTraverse(BiTree T)
{
if(T!=NULL)
{
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
printf("%c",T->data);
}
}
层次遍历
void LayerOrder(BTreeNode *t)
{
//利用队列实现层次遍历,每次访问根结点,然后一次放入左结点和右结点(如果有的话)。
if(t == NULL)return ;
queue<BTreeNode*> q;
BTreeNode *temp;
q.push(t);
while(!q.empty())
{
temp = q.front();
q.pop();
cout<<temp->data<<' ';
if(temp->lchild != NULL)
q.push(temp->lchild);
if(temp->rchild != NULL)
q.push(temp->rchild);
}
}
二叉树的应用
计算叶子结点
void CountLeaf(BiTree T,int &count)
{
if(T!=NULL)
{
if((!T->lchild)&&(!T->rchild))
count++;
CountLeaf(T->lchild,count); //左子树叶子个数
CountLeaf(T->rchild,count); //右子树叶子个数
}
}
计算双结点
void CountParent(BiTree T,int &count)
{
if(T!=NULL)
{
if(T->lchild&&T->rchild)
count++;
CountParent(T->lchild,count); //左子树双结点个数
CountParent(T->rchild,count); //右子树双结点个数
}
}
计算二叉树结点个数
void Count(BiTree T,int &count)
{
if(T)
{
Count(T->lchild,count);
Count(T->rchild,count);
count++; //结点个数
}
}
单结点个数
void CountChild(BiTree T,int &count)
{
if(T)
{
if((T->lchild&&(!T->rchild))||(T->rchild&&(!T->lchild)))
count++;
CountChild(T->lchild,count); //左子树单结点个数
CountChild(T->rchild,count); //右子树单结点个数
}
}
计算树的高度
int GetHeight(BinTree BT)
{
int lhight;
int rhight;
if (BT == NULL)
return 0;
lhight = 1 + GetHeight(BT->Left);
rhight = 1 + GetHeight(BT->Right);
if(lhight>rhight)
return lhight;
else
return rhight;
}
计算任意节点所在层次
int NodeLevel(BiTree T,TElemType &p,int &count)
{
if(T==NULL)
return 0;
if(T->data==p)
return 1;
if(NodeLevel(T->lchild,p,count)||(NodeLevel(T->rchild,p,count)))
{
count++;
return 1;
}
}
交换二叉树左右子树
void Exchange(BiTree &T)
{
BiTree temp;
if (T == NULL)
return;
Exchange(T ->lchild); //交换左子树
Exchange(T ->rchild); //交换右子树
temp = NULL;
temp = T ->lchild; //交换
T->lchild=T->rchild;
T->rchild=temp;
}
判断两树是否相似
int LikeBiTree(BiTree T1,BiTree T2)
{
int like1,like2;
if(T1==NULL&&T2==NULL)
return 1;
else if(T1==NULL||T2==NULL)
return 0;
else
{
like1=LikeBiTree(T1->lchild,T2->lchild);
like2=LikeBiTree(T1->rchild,T2->rchild);
return(like1&&like2);
}
}
树的结构、操作、遍历及应用
树:是一个n(n>=0)个结点的有序合集
结点:指树中的一个元素;
结点的度:指结点拥有的子树的个数,二叉树的度不大于2;
数的度:指树中的最大结点度数;
叶子:度为0的结点,也称为终端结点;
高度:叶子节点的高度为1,根节点高度最高;
层:根在第一层,以此类推;
树的结构
双亲表示法
双亲表示法(父指针表示)采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变量。
如图所示:

typedef struct Snode
{
int data;//树中结点的数据类型
int parent;//结点的父结点在数组中的位置下标
}PTNode;
typedef struct
{
PTNode tnode[MAXSIZE];//存放树中所有结点
int n;//根的位置下标和结点数
}PTree;
孩子表示法
孩子表示法(子女链表示)存储普通树采用的是 "顺序表+链表" 的组合结构,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如图所示:
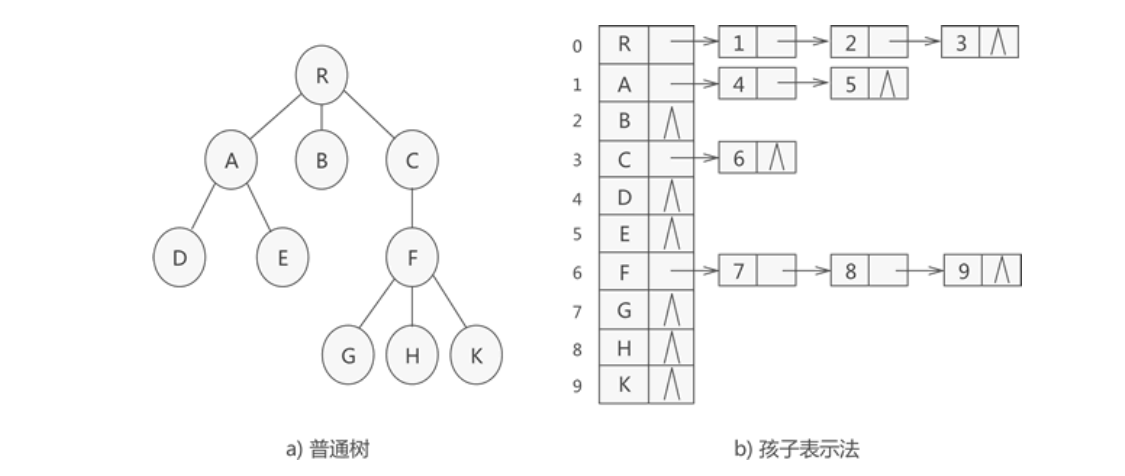
typedef struct CTNode
{
int child;//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
struct CTNode * next;
}ChildPtr;
typedef struct
{
TElemType data;//结点的数据类型
ChildPtr* firstchild;//孩子链表的头指针
}CTBox;
typedef struct
{
CTBox nodes[MAX_SIZE];//存储结点的数组
int n,r;//结点数量和树根的位置
}CTree;
双亲孩子表示法
双亲孩子表示法将双亲表示法和孩子表示法进行有机结合,将各结点的孩子结点分别组成单链表,用一维数组顺序储存树中各结点,数组元素包括结点本身的信息、双亲结点在数组中的序号以及该结点的孩子结点链表的头结点
如图所示:
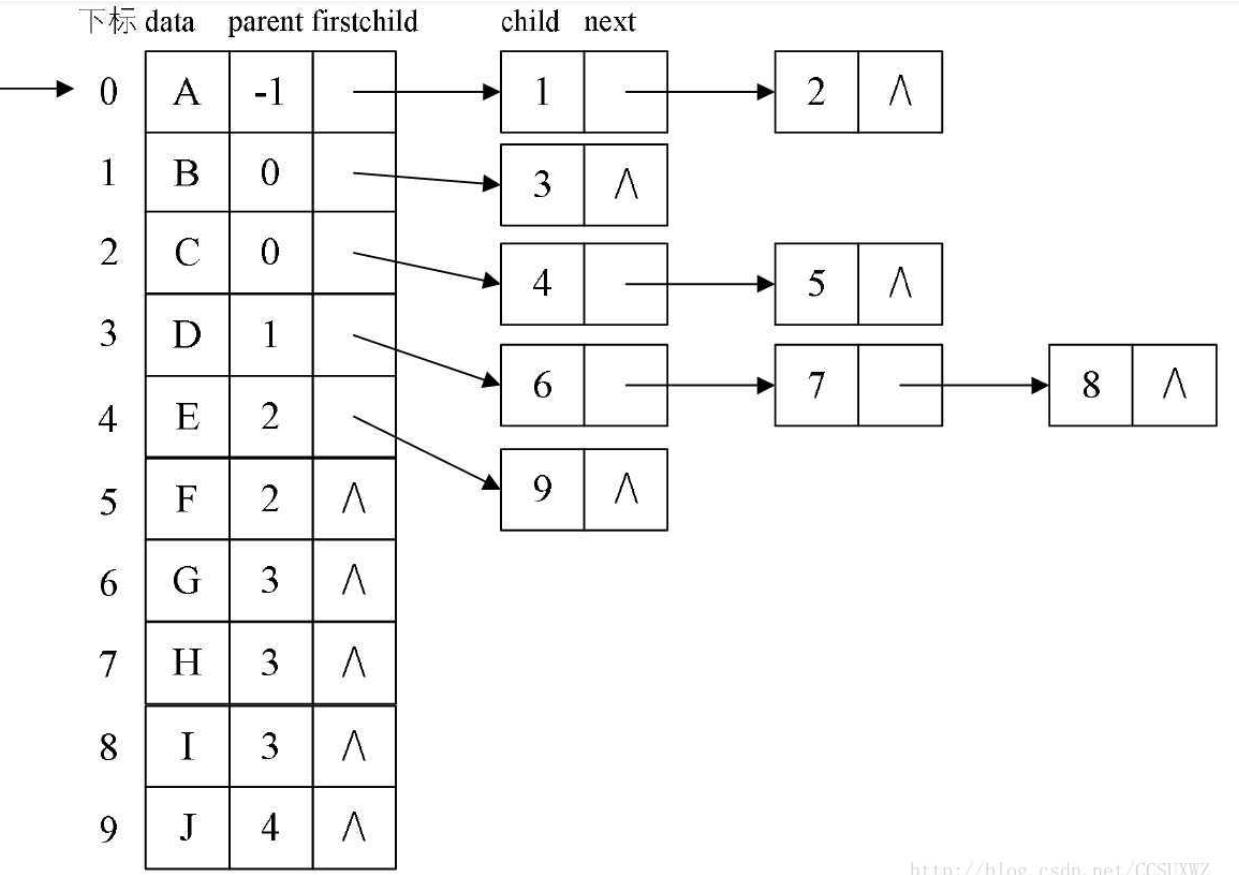
//孩子结点
typedef struct CTNode //定义树中的一个结点
{
int child; //孩子结点的下标
struct CTNode *next; //指向下一个孩子结点的指针
}*ChildPtr;
//表头结构
typedef struct
{
ElemType data; //存放树中结点的数据
int parent; //存放双亲下标
ChildPtr firstchild; //指向第一个孩子的指针
}CTBox;
//树结构
typedef struct
{
CTBox nodes[MAX_TREE_SIZE];
int r; //根的位置索引
int n; //树中结点的总数
}BTree;
孩子兄弟表示法
孩子兄弟表示法(左孩子右兄弟),采用的是链式存储结构,其存储树的实现思想是:从树的根节点开始,依次用链表存储各个节点的孩子节点和兄弟节点。链表中每一个结点都有一个信息域和两个指针域。
如图所示:

ypedef struct CSNode
{
ElemType data;
struct CSNode * child,*brother;
}BTree,*BT;
树的创建
双亲表示法的创建
PTree InitPNode(PTree tree)
{
int i,j;
char ch;
//printf("请输出节点个数:\n");
scanf("%d",&(tree.n));
//printf("请输入结点的值其双亲位于数组中的位置下标:\n");
for(i=0; i<tree.n; i++)
{
fflush(stdin);
scanf("%c %d",&ch,&j);
tree.tnode[i].data = ch;
tree.tnode[i].parent = j;
}
return tree;
}
孩子表示法的创建
CTree initTree(CTree tree)
{
printf("输入节点数量:\n");
scanf("%d",&(tree.n));
for(int i=0;i<tree.n;i++)
{
printf("输入第 %d 个节点的值:\n",i+1);
fflush(stdin);
scanf("%c",&(tree.nodes[i].data));
tree.nodes[i].firstchild=(ChildPtr*)malloc(sizeof(ChildPtr));
tree.nodes[i].firstchild->next=NULL;
printf("输入节点 %c 的孩子节点数量:\n",tree.nodes[i].data);
int Num;
scanf("%d",&Num);
if(Num!=0)
{
ChildPtr * p = tree.nodes[i].firstchild;
for(int j = 0 ;j<Num;j++)
{
ChildPtr * newEle=(ChildPtr*)malloc(sizeof(ChildPtr));
newEle->next=NULL;
printf("输入第 %d 个孩子节点在顺序表中的位置",j+1);
scanf("%d",&(newEle->child));
p->next= newEle;
p=p->next;
}
}
}
return tree;
}
双亲孩子表示法的创建
void InitCtree(CTree &t) //初始化树
{
int i;
printf("请输入树的结点个数:\n");
scanf("\n%d",&t.n);
printf("依次输入各个结点:\n");
for(i=0; i<t.n; i++)
{
fflush(stdin);
t.tree[i].data = getchar();
t.tree[i].r = 0;
t.tree[i].firstchid = NULL;
}
}
void AddChild(CTree &t) //添加孩子
{
int i,j,k;
printf("添加孩子\n");
for(k=0; k<t.n-1; k++)
{
fflush(stdin);
printf("请输入孩子结点及其双亲结点的序号:\n");
scanf("%d,%d",&i,&j);
fflush(stdin);
CNode *p = (CNode *)malloc(sizeof(CNode));
p->childnode = i;
p->nextchild = NULL;
t.tree[i].r = j; //找到双亲
if(!t.tree[j].firstchid)
t.tree[j].firstchid = p;
else
{
CNode *temp = t.tree[j].firstchid;
while(temp->nextchild)
temp = temp->nextchild;
temp->nextchild = p;
}
}
}
孩子兄弟表示法的创建
void creat_cstree(CSTree &T)
{
FILE *fin=fopen("树的孩子兄弟表示法.txt","r");
char fa=' ',ch=' ';
for( fscanf(fin,"%c%c",&fa,&ch); ch!='#'; fscanf(fin,"%c%c",&fa,&ch) )
{
CSTree p=(CSTree)malloc(sizeof(CSTree));
init_cstree(p);
p->data=ch;
q[++count]=p;
if('#' == fa)
T=p;
else
{
CSTree s = (CSTree)malloc(sizeof(CSTree));
int i;
for(i=1;i<=MAXSIZE;i++)
{
if(q[i]->data == fa)
{
s=q[i];
break;
}
}
if(! (s->firstchild) ) //如果该双亲结点还没有接孩子节点
s->firstchild=p;
else //如果该双亲结点已经接了孩子节点
{
CSTree temp=s->firstchild;
while(NULL != temp->nextsibling)
{
temp=temp->nextsibling;
}
temp->nextsibling=p;
}
}
}
fclose(fin);
}
线索二叉树和双向线索二叉树
以中序二叉树为例,我们可以把这颗二叉树中所有空指针域的lchild,改为指向当前结点的前驱,把空指针域中的rchild,改为指向结点的后继(绿色箭头)。我们把指向前驱和后继的指针叫做线索 ,加上线索的二叉树就称之为线索二叉树。每一个结点都增设两个标志域LTag和RTag(LTag为0是指向该结点的左孩子,为1时指向该结点的前驱
RTag为0是指向该结点的右孩子,为1时指向该结点的后继),它们只存放0或1的布尔型变量,占用的空间很小。
结构定义
typedef enum { Link, Thread } PointerTag; //Link==0,表示指向左右孩子指针,Thread==1,表示指向前驱或后继的线索
typedef struct BiThrNode
{
int data; //结点数据
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag;
PointerTag RTag; //左右标志
}BiThrNode, *BiThrTree;
二叉树线索化
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
线索化具体实现过程以及代码实现
以中序二叉树的线索化为例,线索化的具体实现就是将中序二叉树的遍历进行修改,把原本打印函数的代码改为指针修改的代码就可以了。
我们设置一个pre指针,永远指向遍历当前结点的前一个结点。若遍历的当前结点左指针域为空,也就是无左孩子,则把左孩子的指针指向pre(相对当前结点的前驱结点)。
右孩子同样的,当pre的右孩子为空,则把pre右孩子的指针指向当前结点(相对pre结点为后继结点)。
最后把当前结点赋给pre,完成后续的递归遍历线索化。
void InThreading(BiThrTree B,BiThrTree *pre)
{
if(B==NULL)
return;
InThreading(B->lchild,pre);
if(!B->lchild) //没有左孩子
{
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild) //没有右孩子
{
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
InThreading(B->rchild,pre);
}
遍历线索二叉树
bool InOrderTraverse(BiThrTree T)
{
BiThrNode *p = T->lchild;
while(p!=T)
{
while(p->LTag==Link) //走向左子树的尽头
p = p->lchild;
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) //访问该结点的后续结点
{
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return true;
}
双向线索二叉树
在线索二叉树的基础上,额外添加一个结点。此结点的作用类似于链表中的头指针,数据域不起作用,只利用两个指针域(由于都是指针,标志域都为 0 )。左指针域指向二叉树的树根,确保可以正方向对二叉树进行遍历;同时,右指针指向线索二叉树形成的线性序列中的最后一个结点。这样,二叉树中的线索链表就变成了双向线索链表,既可以从第一个结点通过不断地找后继结点进行遍历,也可以从最后一个结点通过不断找前趋结点进行遍历。
如图所示:

构建双向线索二叉树的代码
//建立双向线索链表
void InOrderThread_Head(BiThrTree *h, BiThrTree t)
{
//初始化头结点
(*h) = (BiThrTree)malloc(sizeof(BiThrNode));
if((*h) == NULL)
{
printf("申请内存失败");
return ;
}
(*h)->rchild = *h;
(*h)->Rtag = Link;
//如果树本身是空树
if(t==NULL)
{
(*h)->lchild = *h;
(*h)->Ltag = Link;
}
else
{
pre = *h;//pre指向头结点
(*h)->lchild = t;//头结点左孩子设为树根结点
(*h)->Ltag = Link;
InThreading(t);//线索化二叉树,pre结点作为全局变量,线索化结束后,pre结点指向中序序列中最后一个结点
pre->rchild = *h;
pre->Rtag = Thread;
(*h)->rchild = pre;
}
}
双向线索二叉树的遍历
双向线索二叉树遍历时,如果正向遍历,就从树的根结点开始。整个遍历过程结束的标志是:当从头结点出发,遍历回头结点时,表示遍历结束。
//中序正向遍历双向线索二叉树
void InOrderThraverse_Thr(BiThrTree h)
{
BiThrTree p;
p = h->lchild; //p指向根结点
while(p != h)
{
while(p->Ltag == Link) //当ltag = 0时循环到中序序列的第一个结点
p = p->lchild;
printf("%c ", p->data); //显示结点数据,可以更改为其他对结点的操作
while(p->Rtag == Thread && p->rchild != h)
{
p = p->rchild;
printf("%c ", p->data);
}
p = p->rchild; //p进入其右子树
}
}
逆向遍历线索二叉树的过程即从头结点的右指针指向的结点出发,逐个寻找直接前趋结点,结束标志同正向遍历一样:
//中序逆方向遍历线索二叉树
void InOrderThraverse_Thr(BiThrTree h)
{
BiThrTree p;
p=h->rchild;
while (p!=h)
{
while (p->Rtag==Link)
p=p->rchild;
printf("%c",p->data);
//如果lchild为线索,直接使用,输出
while (p->Ltag==Thread && p->lchild !=h)
{
p=p->lchild;
printf("%c",p->data);
}
p=p->lchild;
}
}
哈夫曼树、并查集
哈夫曼树
哈夫曼树:当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
相关名词解释
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。
构建哈夫曼的过程
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
1.在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
2.在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
3.重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
哈夫曼树的结点结构
typedef struct
{
int weight;//结点权重
int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;
哈夫曼树的算法实现
/HT数组中存放的哈夫曼树,end表示HT数组中存放结点的最终位置,s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int *s1, int *s2)
{
int min1, min2;
//遍历数组初始下标为 1
int i = 1;
//找到还没构建树的结点
while(HT[i].parent != 0 && i <= end){
i++;
}
min1 = HT[i].weight;
*s1 = i;
i++;
while(HT[i].parent != 0 && i <= end){
i++;
}
//对找到的两个结点比较大小,min2为大的,min1为小的
if(HT[i].weight < min1){
min2 = min1;
*s2 = *s1;
min1 = HT[i].weight;
*s1 = i;
}else{
min2 = HT[i].weight;
*s2 = i;
}
//两个结点和后续的所有未构建成树的结点做比较
for(int j=i+1; j <= end; j++)
{
//如果有父结点,直接跳过,进行下一个
if(HT[j].parent != 0){
continue;
}
//如果比最小的还小,将min2=min1,min1赋值新的结点的下标
if(HT[j].weight < min1){
min2 = min1;
min1 = HT[j].weight;
*s2 = *s1;
*s1 = j;
}
//如果介于两者之间,min2赋值为新的结点的位置下标
else if(HT[j].weight >= min1 && HT[j].weight < min2){
min2 = HT[j].weight;
*s2 = j;
}
}
}
//HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
{
if(n<=1) return; // 如果只有一个编码就相当于0
int m = 2*n-1; // 哈夫曼树总节点数,n就是叶子结点
*HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用
HuffmanTree p = *HT;
// 初始化哈夫曼树中的所有结点
for(int i = 1; i <= n; i++)
{
(p+i)->weight = *(w+i-1);
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
for(int i = n+1; i <= m; i++)
{
(p+i)->weight = 0;
(p+i)->parent = 0;
(p+i)->left = 0;
(p+i)->right = 0;
}
//构建哈夫曼树
for(int i = n+1; i <= m; i++)
{
int s1, s2;
Select(*HT, i-1, &s1, &s2);
(*HT)[s1].parent = (*HT)[s2].parent = i;
(*HT)[i].left = s1;
(*HT)[i].right = s2;
(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
}
}
并查集
并查集是由一群集合构成,最开始时所有元素各自单独构成一个集合。当集合中只有一个元素时,这个集合的代表节点即为该元素,该元素的father也是自己。使用哈希表来存并查集中所有集合的所有元素的father信息,记为fatherMap。fatherMap中的一条记录所代表的含义是key节点的father为value节点。每个节点都有father信息。集合代表节点的father为本身。另外还会存储rank信息,该信息只需要集合的代表节点记录,表示该集合中有多少个元素。记为rankMap。当一个集合中有多个节点时,下层节点的father为上层节点,最上层节点的father指向自己,最上层的节点叫做这个集合的代表节点。在并查集中,若要查询一个节点属于哪个集合,就是查这个节点所在集合的代表节点是什么。一个节点通过father信息找到最上面的节点,直到该节点的father是其本身停止,这个节点代表了整个集合。
- 合并(Union):把两个不相交的集合合并为一个集合。
- 查询(Find):查询两个元素是否在同一个集合中。
初始化
假如有编号为1, 2, 3, ..., n的n个元素,我们用一个数组father[]来存储每个元素的父节点(因为每个元素有且只有一个父节点,所以这是可行的)。一开始,我们先将它们的父节点设为自己。
int father[MAXN];
void init(int n)
{
for (int i = 1; i <= n; ++i)
father[i] = i;
}
查询
我们用递归的写法实现对代表元素的查询:一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)。要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。
int find(int x)
{
if(father[x] == x)
return x;
else
return find(father[x]);
}
合并
先找到两个集合的代表元素,然后将前者的父节点设为后者即可。当然也可以将后者的父节点设为前者,这里暂时不重要。本文末尾会给出一个更合理的比较方法。
void merge(int i, int j)
{
father[find(i)] = find(j);
}
路径压缩
只要在查询的过程中,把沿途的每个节点的父节点都设为根节点即可。下一次再查询时,我们就可以省很多事。这用递归的写法很容易实现.
int find(int x)
{
if(x == father[x])
return x;
else{
father[x] = find(fatjer[x]); //父节点设为根节点
return father[x]; //返回父节点
}
}
按秩合并
把简单的树往复杂的树上合并,而不是相反。因为这样合并后,到根节点距离变长的节点个数比较少。用一个数组rank[]记录每个根节点对应的树的深度(如果不是根节点,其rank相当于以它作为根节点的子树的深度)。一开始,把所有元素的rank(秩)设为1。合并时比较两个根节点,把rank较小者往较大者上合并。值得注意的是,按秩合并会带来额外的空间复杂度。
//初始化
void init(int n)
{
for (int i = 1; i <= n; ++i)
{
father[i] = i;
rank[i] = 1;
}
}
//合并
void merge(int i, int j)
{
int x = find(i), y = find(j); //先找到两个根节点
if (rank[x] <= rank[y])
father[x] = y;
else
father[y] = x;
if (rank[x] == rank[y] && x!=y)
rank[y]++; //如果深度相同且根节点不同,则新的根节点的深度+1
}
哈夫曼编码
Huffman是一种前缀编码;Huffman编码是建立在Huffman树的基础上进行的,因此为了进行Huffman编码,必须先构建Huffman树;树的路径长度是每个叶节点到根节点的路径之和;带权路径长度是(每个叶节点的路径长度*wi)之和;Huffman树是最小带权路径长度的二叉树;构造完Huffman树之后,就可以进行Huffman编码了,编码规则:左分支填0,右分支填1;
哈夫曼编码就是哈夫曼树在电讯通信中的应用之一。广泛的用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。在电讯通信业务中,通常用二进制编码来表示字母或其他字符,并用这样的编码来表示字符序列。
例:如果需传送的电文为 ‘ABACCDA’,它只用到四种字符,用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10, 11,则上述电文便为 ‘00010010101100’(共 14 位),译码员按两位进行分组译码,便可恢复原来的电文。
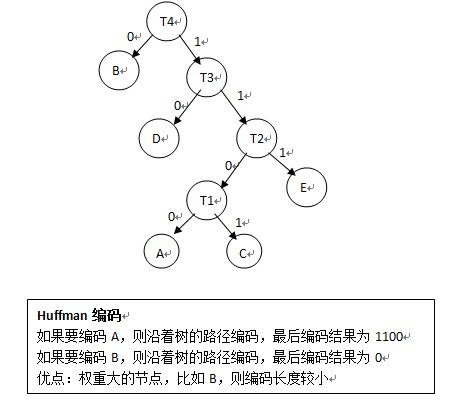
Huffman解码过程:给定一个01串,将01串进行Huffman树,到叶子节点了就表明已经解码一个节点,然后再次遍历Huffman树;
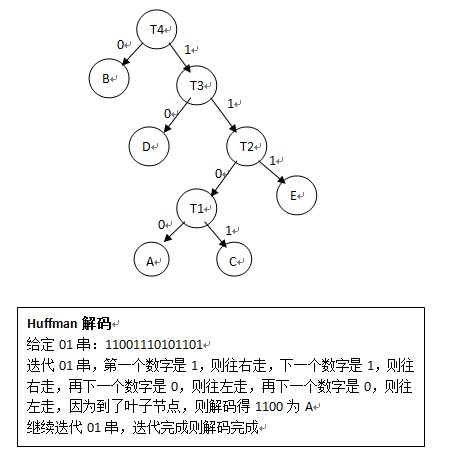
回溯算法
回溯算法,又称为“试探法”。解决问题时,每进行一步,都是抱着试试看的态度,如果发现当前选择并不是最好的,或者这么走下去肯定达不到目标,立刻做回退操作重新选择。这种走不通就回退再走的方法就是回溯算法。
例如,在解决列举集合 {1,2,3} 中所有子集的问题中,就可以使用回溯算法。从集合的开头元素开始,对每个元素都有两种选择:取还是舍。当确定了一个元素的取舍之后,再进行下一个元素,直到集合最后一个元素。其中的每个操作都可以看作是一次尝试,每次尝试都可以得出一个结果。将得到的结果综合起来,就是集合的所有子集。
实现代码为:
#include <stdio.h>
//设置一个数组,数组的下标表示集合中的元素,所以数组只用下标为1,2,3的空间
int set[5];
//i代表数组下标,n表示集合中最大的元素值
void PowerSet(int i,int n)
{
//当i>n时,说明集合中所有的元素都做了选择,开始判断
if (i>n)
{
for (int j=1; j<=n; j++)
{
//如果树组中存放的是 1,说明在当初尝试时,选择取该元素,即对应的数组下标,所以,可以输出
if (set[j]==1)
printf("%d ",j);
}
printf("\n");
}
else
{
//如果选择要该元素,对应的数组单元中赋值为1;反之,赋值为0。然后继续向下探索
set[i]=1;PowerSet(i+1, n);
set[i]=0;PowerSet(i+1, n);
}
}
int main()
{
int n=3;
for (int i=0; i<5; i++)
set[i]=0;
PowerSet(1, n);
return 0;
}
回溯和递归
很多人认为回溯和递归是一样的,其实不然。在回溯法中可以看到有递归的身影,但是两者是有区别的。
回溯法从问题本身出发,寻找可能实现的所有情况。和穷举法的思想相近,不同在于穷举法是将所有的情况都列举出来以后再一一筛选,而回溯法在列举过程如果发现当前情况根本不可能存在,就停止后续的所有工作,返回上一步进行新的尝试。
递归是从问题的结果出发,例如求 n!,要想知道 n!的结果,就需要知道 n(n-1)! 的结果,而要想知道 (n-1)! 结果,就需要提前知道 (n-1)(n-2)!。这样不断地向自己提问,不断地调用自己的思想就是递归。
回溯和递归唯一的联系就是,回溯法可以用递归思想实现。
回溯算法的实现过程
使用回溯法解决问题的过程,实际上是建立一棵“状态树”的过程。例如,在解决列举集合{1,2,3}所有子集的问题中,对于每个元素,都有两种状态,取还是舍,所以构建的状态树为:

回溯算法的求解过程实质上是先序遍历“状态树”的过程。树中每一个叶子结点,都有可能是问题的答案。图 1 中的状态树是满二叉树,得到的叶子结点全部都是问题的解。
在某些情况下,回溯算法解决问题的过程中创建的状态树并不都是满二叉树,因为在试探的过程中,有时会发现此种情况下,再往下进行没有意义,所以会放弃这条死路,回溯到上一步。在树中的体现,就是在树的最后一层不是满的,即不是满二叉树,需要自己判断哪些叶子结点代表的是正确的结果。
广义表
广义表,又称列表,也是一种线性存储结构。同数组类似,广义表中既可以存储不可再分的元素,也可以存储广义表,记作: LS = (a1,a2,…,an),其中,LS 代表广义表的名称,an 表示广义表存储的数据。广义表中每个 ai 既可以代表单个元素,也可以代表另一个广义表。
原子和子表
通常,广义表中存储的单个元素称为 "原子",而存储的广义表称为 "子表"。例如创建一个广义表 LS = {1,{1,2,3}},我们可以这样解释此广义表的构成:广义表 LS 存储了一个原子 1 和子表 {1,2,3}。
以下是广义表存储数据的一些常用形式:
A = ():A 表示一个广义表,只不过表是空的。
B = (e):广义表 B 中只有一个原子 e。
C = (a,(b,c,d)) :广义表 C 中有两个元素,原子 a 和子表 (b,c,d)。
D = (A,B,C):广义表 D 中存有 3 个子表,分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
E = (a,E):广义表 E 中有两个元素,原子 a 和它本身。这是一个递归广义表,等同于:E = (a,(a,(a,…)))。
注意,A = () 和 A = (()) 是不一样的。前者是空表,而后者是包含一个子表的广义表,只不过这个子表是空表。
广义表的表头和表尾
当广义表不是空表时,称第一个数据(原子或子表)为"表头",剩下的数据构成的新广义表为"表尾"。除非广义表为空表,否则广义表一定具有表头和表尾,且广义表的表尾一定是一个广义表。例如在广义表中 LS={1,{1,2,3},5} 中,表头为原子 1,表尾为子表 {1,2,3} 和原子 5 构成的广义表,即 {{1,2,3},5}。再比如,在广义表 LS = {1} 中,表头为原子 1 ,但由于广义表中无表尾元素,因此该表的表尾是一个空表,用 {} 表示。
广义表的储存结构
由于广义表中既可存储原子(不可再分的数据元素),也可以存储子表,因此很难使用顺序存储结构表示,通常情况下广义表结构采用链表实现。使用顺序表实现广义表结构,不仅需要操作 n 维数组(例如 {1,{2,{3,4}}} 就需要使用三维数组存储),还会造成存储空间的浪费。使用链表存储广义表,首先需要确定链表中节点的结构。由于广义表中可同时存储原子和子表两种形式的数据,因此链表节点的结构也有两种。
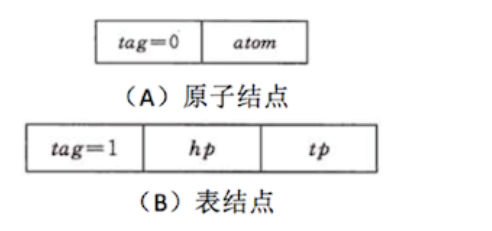
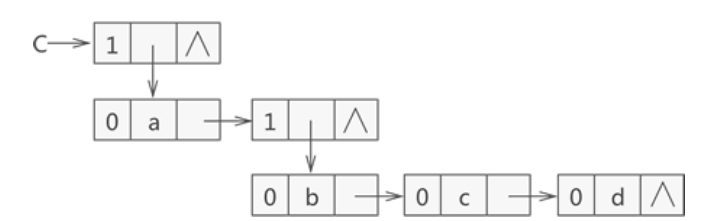
如图所示,表示原子的节点由两部分构成,分别是 tag 标记位和原子的值,表示子表的节点由三部分构成,分别是 tag 标记位、hp 指针和 tp 指针。tag 标记位用于区分此节点是原子还是子表,通常原子的 tag 值为 0,子表的 tag 值为 1。子表节点中的 hp 指针用于连接本子表中存储的原子或子表,tp 指针用于连接广义表中下一个原子或子表。
typedef struct GLNode
{
int tag;//标志域
union
{
char atom;//原子结点的值域
struct
{
struct GLNode * hp,*tp;
}ptr;//子表结点的指针域,hp指向表头;tp指向表尾
};
}*Glist;
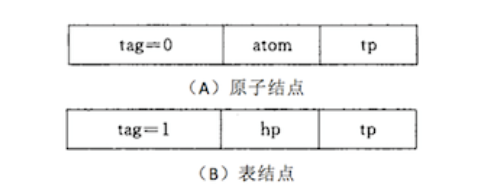
如图所示,表示原子的节点构成由 tag 标记位、原子值和 tp 指针构成,表示子表的节点还是由 tag 标记位、hp 指针和 tp 指针构成。
typedef struct GLNode
{
int tag;//标志域
union
{
int atom;//原子结点的值域
struct GLNode *hp;//子表结点的指针域,hp指向表头
};
struct GLNode * tp;//这里的tp相当于链表的next指针,用于指向下一个数据元素
}*Glist;
广义表的创建
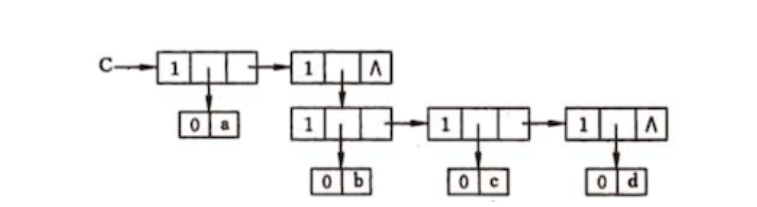
Glist creatGlist(Glist C)
{
//广义表C
C=(Glist)malloc(sizeof(Glist));
C->tag=1;
//表头原子‘a’
C->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.hp->tag=0;
C->ptr.hp->atom='a';
//表尾子表(b,c,d),是一个整体
C->ptr.tp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->tag=1;
C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.tp=NULL;
//开始存放下一个数据元素(b,c,d),表头为‘b’,表尾为(c,d)
C->ptr.tp->ptr.hp->tag=1;
C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.hp->atom='b';
C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(Glist));
//存放子表(c,d),表头为c,表尾为d
C->ptr.tp->ptr.hp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(Glist));
//存放表尾d
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
return C;
}
Glist creatGlist(Glist C)
{
C=(Glist)malloc(sizeof(Glist));
C->tag=1;
C->hp=(Glist)malloc(sizeof(Glist));
C->tp=NULL;
//表头原子a
C->hp->tag=0;
C->atom='a';
C->hp->tp=(Glist)malloc(sizeof(Glist));
C->hp->tp->tag=1;
C->hp->tp->hp=(Glist)malloc(sizeof(Glist));
C->hp->tp->tp=NULL;
//原子b
C->hp->tp->hp->tag=0;
C->hp->tp->hp->atom='b';
C->hp->tp->hp->tp=(Glist)malloc(sizeof(Glist));
//原子c
C->hp->tp->hp->tp->tag=0;
C->hp->tp->hp->tp->atom='c';
C->hp->tp->hp->tp->tp=(Glist)malloc(sizeof(Glist));
//原子d
C->hp->tp->hp->tp->tp->tag=0;
C->hp->tp->hp->tp->tp->atom='d';
C->hp->tp->hp->tp->tp->tp=NULL;
return C;
}
广义表的深度和长度
长度
广义表的长度,指的是广义表中所包含的数据元素的个数。由于广义表中可以同时存储原子和子表两种类型的数据,因此在计算广义表的长度时规定,广义表中存储的每个原子算作一个数据,同样每个子表也只算作是一个数据。广义表规定,空表 {} 的长度为 0。
#include <stdio.h>
#include <stdlib.h>
typedef struct GLNode{
int tag;//标志域
union{
char atom;//原子结点的值域
struct{
struct GLNode * hp,*tp;
}ptr;//子表结点的指针域,hp指向表头;tp指向表尾
};
}*Glist;
Glist creatGlist(Glist C){
//广义表C
C=(Glist)malloc(sizeof(Glist));
C->tag=1;
//表头原子‘a’
C->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.hp->tag=0;
C->ptr.hp->atom='a';
//表尾子表(b,c,d),是一个整体
C->ptr.tp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->tag=1;
C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.tp=NULL;
//开始存放下一个数据元素(b,c,d),表头为‘b’,表尾为(c,d)
C->ptr.tp->ptr.hp->tag=1;
C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.hp->atom='b';
C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(Glist));
//存放子表(c,d),表头为c,表尾为d
C->ptr.tp->ptr.hp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(Glist));
//存放表尾d
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(Glist));
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
return C;
}
int GlistLength(Glist C){
int Number=0;
Glist P=C;
while(P){
Number++;
P=P->ptr.tp;
}
return Number;
}
int main(){
Glist C = creatGlist(C);
printf("广义表的长度为:%d",GlistLength(C));
return 0;
}
深度
广义表的深度,可以通过观察该表中所包含括号的层数间接得到。观察括号的方法需将广义表当做字符串看待,并借助栈存储结构实现。
#include <stdio.h>
#include <stdlib.h>
typedef struct GLNode
{
int tag;//标志域
union
{
char atom;//原子结点的值域
struct
{
struct GLNode * hp,*tp;
}ptr;//子表结点的指针域,hp指向表头;tp指向表尾
};
}*Glist,GNode;
Glist creatGlist(Glist C)
{
//广义表C
C=(Glist)malloc(sizeof(GNode));
C->tag=1;
//表头原子‘a’
C->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.hp->tag=0;
C->ptr.hp->atom='a';
//表尾子表(b,c,d),是一个整体
C->ptr.tp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->tag=1;
C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.tp=NULL;
//开始存放下一个数据元素(b,c,d),表头为‘b’,表尾为(c,d)
C->ptr.tp->ptr.hp->tag=1;
C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.hp->atom='b';
C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(GNode));
//存放子表(c,d),表头为c,表尾为d
C->ptr.tp->ptr.hp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(GNode));
//存放表尾d
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
return C;
}
int GlistDepth(Glist C)
{
//如果表C为空表时,直接返回长度1;
if (!C)
return 1;
//如果表C为原子时,直接返回0;
if (C->tag==0)
return 0;
int max=0;//设置表C的初始长度为0;
for (Glist pp=C; pp; pp=pp->ptr.tp)
{
int dep=GlistDepth(pp->ptr.hp);
if (dep>max)
max=dep;//每次找到表中遍历到深度最大的表,并用max记录
}
//程序运行至此处,表明广义表不是空表,由于原子返回的是0,而实际长度是1,所以,此处要+1;
return max+1;
}
int main(int argc, const char * argv[])
{
Glist C=creatGlist(C);
printf("广义表的深度为:%d",GlistDepth(C));
return 0;
}
广义表的复制
对于任意一个非空广义表来说,都是由两部分组成:表头和表尾。反之,只要确定的一个广义表的表头和表尾,那么这个广义表就可以唯一确定下来。复制一个广义表,也是不断的复制表头和表尾的过程。如果表头或者表尾同样是一个广义表,依旧复制其表头和表尾。
递归的出口有两个:
- 如果当前遍历的数据元素为空表,则直接返回空表。
- 如果当前遍历的数据元素为该表的一个原子,那么直接复制,返回即可。
#include <stdio.h>
#include <stdlib.h>
typedef struct GLNode
{
int tag;//标志域
union
{
char atom;//原子结点的值域
struct
{
struct GLNode * hp,*tp;
}ptr;//子表结点的指针域,hp指向表头;tp指向表尾
};
}*Glist,GNode;
Glist creatGlist(Glist C)
{
//广义表C
C=(Glist)malloc(sizeof(GNode));
C->tag=1;
//表头原子‘a’
C->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.hp->tag=0;
C->ptr.hp->atom='a';
//表尾子表(b,c,d),是一个整体
C->ptr.tp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->tag=1;
C->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.tp=NULL;
//开始存放下一个数据元素(b,c,d),表头为‘b’,表尾为(c,d)
C->ptr.tp->ptr.hp->tag=1;
C->ptr.tp->ptr.hp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.hp->atom='b';
C->ptr.tp->ptr.hp->ptr.tp=(Glist)malloc(sizeof(GNode));
//存放子表(c,d),表头为c,表尾为d
C->ptr.tp->ptr.hp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.hp->atom='c';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp=(Glist)malloc(sizeof(GNode));
//存放表尾d
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->tag=1;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp=(Glist)malloc(sizeof(GNode));
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->tag=0;
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.hp->atom='d';
C->ptr.tp->ptr.hp->ptr.tp->ptr.tp->ptr.tp=NULL;
return C;
}
void copyGlist(Glist C, Glist *T){
//如果C为空表,那么复制表直接为空表
if (!C)
*T=NULL;
else
{
*T=(Glist)malloc(sizeof(GNode));//C不是空表,给T申请内存空间
//申请失败,程序停止
if (!*T)
exit(0);
(*T)->tag=C->tag;//复制表C的tag值
//判断当前表元素是否为原子,如果是,直接复制
if (C->tag==0)
(*T)->atom=C->atom;
else //运行到这,说明复制的是子表
{
copyGlist(C->ptr.hp, &((*T)->ptr.hp));//复制表头
copyGlist(C->ptr.tp, &((*T)->ptr.tp));//复制表尾
}
}
}
int main(int argc, const char * argv[])
{
Glist C=NULL;
C=creatGlist(C);
Glist T=NULL;
copyGlist(C,&T);
printf("%c",T->ptr.hp->atom);
return 0;
}
红黑树
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
特性
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
红黑树的结构定义
// 红黑树的节点
typedef struct RBTreeNode
{
unsigned char color; // 颜色(RED 或 BLACK)
Type key; // 关键字(键值)
struct RBTreeNode *left; // 左孩子
struct RBTreeNode *right; // 右孩子
struct RBTreeNode *parent; // 父结点
}Node, *RBTree;
// 红黑树的根
typedef struct rb_root{
Node *node;
}RBRoot;
红黑树的旋转
当在对红黑树进行插入和删除等操作时,对树做了修改可能会破坏红黑树的性质。为了继续保持红黑树的性质,可以通过对结点进行重新着色,以及对树进行相关的旋转操作,即通过修改树中某些结点的颜色及指针结构,来达到对红黑树进行插入或删除结点等操作后继续保持它的性质或平衡的目的。 树的旋转分为左旋和右旋,下面借助图来介绍一下左旋和右旋这两种操作。
左旋

对x进行左旋,意味着"将x变成一个左节点"。
static void rbtree_left_rotate(RBRoot *root, Node *x)
{
// 设置x的右孩子为y
Node *y = x->right;
// 将 “y的左孩子” 设为 “x的右孩子”;
// 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲”
x->right = y->left;
if (y->left != NULL)
y->left->parent = x;
// 将 “x的父亲” 设为 “y的父亲”
y->parent = x->parent;
if (x->parent == NULL)
{
//tree = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
root->node = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
}
else
{
if (x->parent->left == x)
x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else
x->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
}
// 将 “x” 设为 “y的左孩子”
y->left = x;
// 将 “x的父节点” 设为 “y”
x->parent = y;
}
右旋
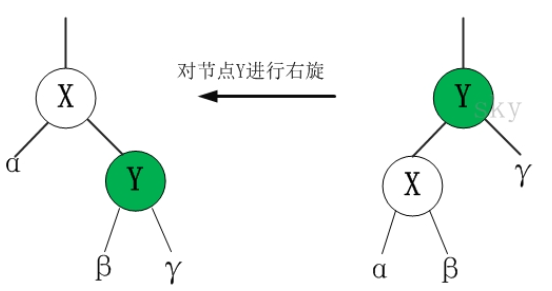
对y进行左旋,意味着"将y变成一个右节点"。
static void rbtree_right_rotate(RBRoot *root, Node *y)
{
// 设置x是当前节点的左孩子。
Node *x = y->left;
// 将 “x的右孩子” 设为 “y的左孩子”;
// 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”
y->left = x->right;
if (x->right != NULL)
x->right->parent = y;
// 将 “y的父亲” 设为 “x的父亲”
x->parent = y->parent;
if (y->parent == NULL)
{
//tree = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
root->node = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
}
else
{
if (y == y->parent->right)
y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
else
y->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
}
// 将 “y” 设为 “x的右孩子”
x->right = y;
// 将 “y的父节点” 设为 “x”
y->parent = x;
}
红黑树的添加
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
第二步:将插入的节点着色为"红色"。
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
static void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node *parent, *gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while ((parent = rb_parent(node)) && rb_is_red(parent))
{
gparent = rb_parent(parent);
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent->left)
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->right;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent->right == node)
{
Node *tmp;
rbtree_left_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
rb_set_black(parent);
rb_set_red(gparent);
rbtree_right_rotate(root, gparent);
}
else//若“z的父节点”是“z的祖父节点的右孩子”
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->left;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent->left == node)
{
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
rb_set_black(parent);
rb_set_red(gparent);
rbtree_left_rotate(root, gparent);
}
}
// 将根节点设为黑色
rb_set_black(root->node);
}
红黑树的删除
第一步:将红黑树当作一颗二叉查找树,将节点删除。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
{
Node *other;
while ((!node || rb_is_black(node)) && node != root->node)
{
if (parent->left == node)
{
other = parent->right;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
rbtree_left_rotate(root, parent);
other = parent->right;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->right || rb_is_black(other->right))
{
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
rb_set_black(other->left);
rb_set_red(other);
rbtree_right_rotate(root, other);
other = parent->right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->right);
rbtree_left_rotate(root, parent);
node = root->node;
break;
}
}
else
{
other = parent->left;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
rbtree_right_rotate(root, parent);
other = parent->left;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->left || rb_is_black(other->left))
{
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
rb_set_black(other->right);
rb_set_red(other);
rbtree_left_rotate(root, other);
other = parent->left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->left);
rbtree_right_rotate(root, parent);
node = root->node;
break;
}
}
}
if (node)
rb_set_black(node);
}
平衡二叉树
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
LL型:在A结点左子树根结点的左子树插入结点,导致A结点平衡因子由1变2。进行一次顺时针旋转;将原根结点的左孩子作为新生成树的根结点,将左孩子的右子树作为原树根结点的左孩子。
RR型:在A结点右子树根结点的右子树插入结点,导致A结点平衡因子由-1变-2。 进行一次逆时针旋转;将原根结点的右孩子作为新生成树的根结点,将右孩子的左子树作为原树根结点的右孩子。
LR型:在A结点左子树根结点的右子树插入结点,导致A结点平衡因子由1变2。先逆时针旋转一次,后顺时针旋转一次;将新插入的部分作为此插入结点父节点的右孩子,逆时针旋转一次,将此结点作为此子树的根结点,将其原父节点作为此结点的左孩子,再将此结点的右孩子作为原树根结点的左孩子,顺时针旋转一次,将此结点作为整个树的根结点,将原根结点作为新生成树的右孩子。
RL型:在A结点右子树根结点的左子树插入结点,导致A结点平衡因子由-1变-2。先顺时针旋转一次,后逆时针旋转一次;将新插入的部分作为此插入结点父节点的左孩子,顺时针旋转一次,将此结点作为此子树的根结点,将其原父节点作为此结点的右孩子,再将此结点的左孩子作为原树根结点的右孩子,逆时针旋转一次,将此结点作为整颗树的根结点,将原根结点作为新生成树的左孩子。
平衡二叉树的结点结构
template <typename T>
struct AvlNode
{
T data;
int height; //结点所在高度
AvlNode<T> *left;
AvlNode<T> *right;
AvlNode<T>(const T theData) : data(theData), left(NULL), right(NULL), height(0){}
};
平衡二叉树不平衡的情况
把需要重新平衡的结点叫做α,由于任意两个结点最多只有两个儿子,因此高度不平衡时,α结点的两颗子树的高度相差2.容易看出,这种不平衡可能出现在下面4中情况中:
1.对α的左儿子的左子树进行一次插入
2.对α的左儿子的右子树进行一次插入
3.对α的右儿子的左子树进行一次插入
4.对α的右儿子的右子树进行一次插入
如图所示:
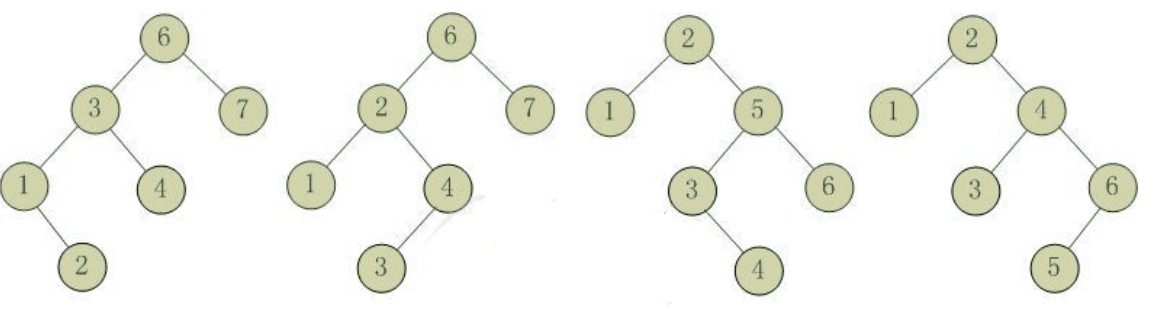
平衡二叉树的单旋转
左左插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::LL(AvlNode<T> *t)
{
AvlNode<T> *q = t->left;
t->left = q->right;
q->right = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
右右插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::RR(AvlNode<T> *t)
{
AvlNode<T> *q = t->right;
t->right = q->left;
q->left = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
平衡二叉树的双旋转
插入点位于t的左儿子的右子树
template <typename T>
AvlNode<T> * AvlTree<T>::LR(AvlNode<T> *t)
{
//双旋转可以通过两次单旋转实现
//对t的左结点进行RR旋转,再对根节点进行LL旋转
RR(t->left);
return LL(t);
}
插入点位于t的右儿子的左子树
template <typename T>
AvlNode<T> * AvlTree<T>::RL(AvlNode<T> *t)
{
LL(t->right);
return RR(t);
}
平衡二叉树的删除结点
template <typename T>
bool AvlTree<T>::Delete(AvlNode<T> *&t, T x)
{
//t为空 未找到要删除的结点
if (t == NULL)
return false;
//找到了要删除的结点
else if (t->data == x)
{
//左右子树都非空
if (t->left != NULL && t->right != NULL) //在高度更大的那个子树上进行删除操作
{
if (GetHeight(t->left) > GetHeight(t->right)) //左子树高度大,删除左子树中值最大的结点,将其赋给根结点
{
t->data = FindMax(t->left)->data;
Delete(t->left, t->data);
}
else//右子树高度更大,删除右子树中值最小的结点,将其赋给根结点
{
t->data = FindMin(t->right)->data;
Delete(t->right, t->data);
}
}
else //左右子树有一个不为空,直接用需要删除的结点的子结点替换即可
{
AvlNode<T> *old = t;
t = t->left ? t->left: t->right;//t赋值为不空的子结点
delete old;
}
}
else if (x < t->data)//要删除的结点在左子树上
{
Delete(t->left, x); //递归删除左子树上的结点
if (GetHeight(t->right) - GetHeight(t->left) > 1) //判断是否仍然满足平衡条件
{
if (GetHeight(t->right->left) > GetHeight(t->right->right))
t = RL(t); //RL双旋转
else
t = RR(t); //RR单旋转
}
else//满足平衡条件 调整高度信息
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
else//要删除的结点在右子树上
{
Delete(t->right, x); //递归删除右子树结点
if (GetHeight(t->left) - GetHeight(t->right) > 1) //判断平衡情况
{
if (GetHeight(t->left->right) > GetHeight(t->left->left))
t = LR(t); //LR双旋转
else
t = LL(t); //LL单旋转
}
else//满足平衡性 调整高度
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
return true;
}
平衡二叉树查找结点
template <typename T>
bool AvlTree<T>::Contains(AvlNode<T> *t, const T x) const
{
if (t == NULL)
return false;
if (x < t->data)
return Contains(t->left, x);
else if (x > t->data)
return Contains(t->right, x);
else
return true;
}
平衡二叉树查找最大值结点
template <typename T>
AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const
{
if (t == NULL)
return NULL;
if (t->right == NULL)
return t;
return FindMax(t->right);
}
平衡二叉树查找最小值结点
template <typename T>
AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const
{
if (t == NULL)
return NULL;
if (t->left == NULL)
return t;
return FindMin(t->left);
}
平衡二叉树求树的高度
template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T> *t)
{
if (t == NULL)
return -1;
else
return t->height;
}
平衡二叉树的插入结点
template <typename T>
void AvlTree<T>::Insert(AvlNode<T> *&t, T x)
{
if (t == NULL)
t = new AvlNode<T>(x);
else if (x < t->data)
{
Insert(t->left, x);
if (GetHeight(t->left) - GetHeight(t->right) > 1)//判断平衡情况
{
if (x < t->left->data)//左左
t = LL(t);
else //左右
t = LR(t);
}
}
else if (x > t->data)
{
Insert(t->right, x);
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
if (x > t->right->data)
t = RR(t);
else
t = RL(t);
}
}
else
;//数据重复
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
1.2.谈谈你对树的认识及学习体会。
- 不同类型的树之间是可以相互转化的,比如一颗普通的树可以通过特定的过程转化成二叉树,也可以转化成森林,反之亦然。树也存在着多种的存储结构,例如:双亲存储,孩子链存储,孩子兄弟存储。二叉树是最常见的树,我们详细的学历了二叉树的创建、消除等等基本构造二叉树的方法,也学习了如何用先序加中序,中序加后序来进行树的构建。通过二叉树的学习,我们又学习了线索二叉树,和哈夫曼树,这两个知识点都是在二叉树的基础上进行升华的。线索二叉树可以轻易的得到该结点的相邻的结点,而哈夫曼树则可以用来求解最优解的问题。
- 树形结构属于非线性结构,常用的树形结构有树和二叉树。树是由n(n>=1)个有限节点组成一个具有层次关系的集合。树的基本术语有:结点的度与树的度;分支节点与叶子结点;路径与路径长度;孩子结点、双亲结点和兄弟结点;结点层次和树的高度等等。树有多种类型,可分为二叉树和哈夫曼树等,其中二叉树又可分为完全二叉树和满二叉树。 在树中主要学习了二叉树和哈夫曼树这种树。
- 二叉树:二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子。二叉树的存储结构可以有顺序存储结构和连式存储结构。可以通过二叉树的疏密以及题目要求等来决定树的存储结构。二叉树遍历的方法有先序遍历、中序遍历、后序遍历与层次遍历四种方法。不论在树的建立或其他基本运算中基本是要运用到递归,代码量少,但是理解起来不容易,而且错误地方不容易调试看出来。
- 树的学习还是学的更懵逼了,特别是一开始递归部分不好理解,而且这章节需要记住的知识点很多,孩子节点、兄弟节点、满二叉树、完全二叉树等等一堆东西,我觉得我脑子已经不够用了,PTA上的题目以及不友好了,特别是表达式、目录树还有一堆的编程题,还有需要递归的地方,这学期真是不容易啊,学的要死要活的
2.阅读代码
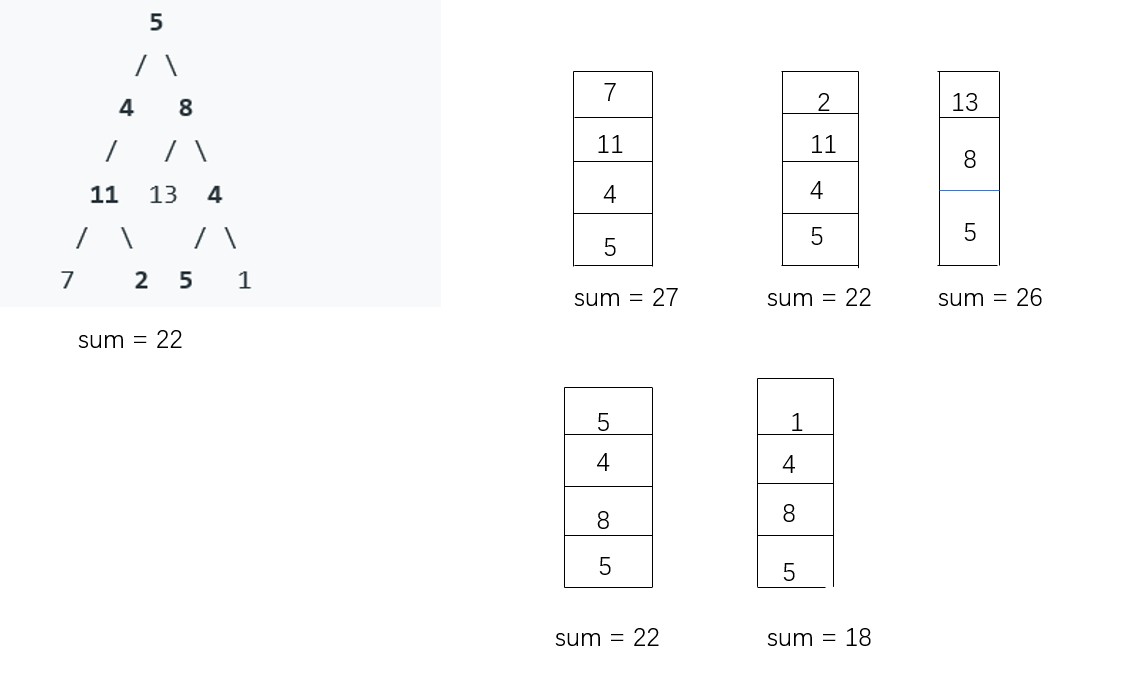
2.1 路径总和
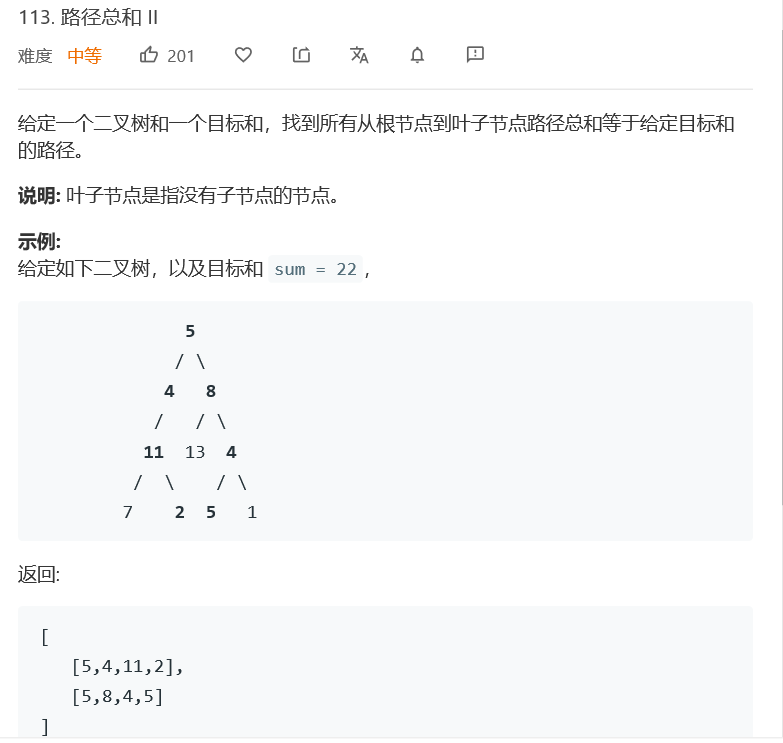
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> ans;
void dfs(TreeNode* root, int sum, vector<int> temp){
temp.push_back(root->val);
if(root->left == NULL && root->right == NULL){
int s = 0;
for(auto n: temp) s += n;
if(s == sum) ans.push_back(temp);
}
if(root->left) dfs(root->left, sum, temp);
if(root->right) dfs(root->right, sum, temp);
}
vector<vector<int>> pathSum(TreeNode* root, int sum) {
if(root == NULL) return ans;
dfs(root, sum, {});
return ans;
}
};
2.1.1 该题的设计思路
1.用临时数组记录当前路径上所有节点的值(递归实现)
2.当访问记录到叶子节点,计算路径总和。记录符合要求的路径
2.1.2 该题的伪代码
dfs(root,sum,temp)函数
{
temp.push_back(root->val)
if(temp的左右孩子都为空)
定义s=0
for (auto n : temp)
s += n;
if(s和sum相等)
ans.push_back(temp)
end if
end if
if(root左孩子不为空)
dfs(root->left,sum,temp)
end if
if(root右孩子不为空)
dfs(root->right,sum,temp)
end if
}
pathSum(root,sum)函数
{
if(root为空)
return ans
end if
dfs(root,sum,{})
return ans
}
2.1.3 运行结果
2.1.4分析该题目解题优势及难点。
- 优势:运用递归解法并把满足题目要求的路径储存到迭代器中
- 难点:如果用普通数组储存一条满足题意的路径,需要进行不断的更新删除替换,解题代码就灵活运用迭代器和队列的结合,可以做到很好的删除更新
2.2 玩转二叉树
#include<iostream>
#include<stdlib.h>
#include<queue>
using namespace std;
typedef struct TNode
{
int data;
struct TNode *left;
struct TNode *right;
}*BinTree;
BinTree create(int pre[], int mid[], int len)
{
if (len == 0)
return NULL;
BinTree bt = (BinTree)malloc(sizeof(struct TNode));
bt->data = pre[0];
int i;
for (i = 0; mid[i] != pre[0]; i++);
bt->left = create(pre + 1, mid, i);
bt->right = create(pre + i + 1, mid + i + 1, len - i - 1);
return bt;
}
void mirror(BinTree& bt)
{
BinTree node = (BinTree)malloc(sizeof(struct TNode));
node = bt->left;
bt->left = bt->right;
bt->right = node;
if (bt->left != NULL)
mirror(bt->left);
if (bt->right != NULL)
mirror(bt->right);
}
void lo(BinTree bt)
{
int flag = 0;
queue<BinTree> q;
q.push(bt);
while (!q.empty())
{
BinTree node = q.front();
q.pop();
if (flag == 0)
{
cout << node->data;
flag = 1;
}
else
cout << ' ' << node->data;
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
int main()
{
int n, pre[31], mid[30];
cin >> n;
for (int i = 0; i < n; i++)
cin >> mid[i];
for (int i = 0; i < n; i++)
cin >> pre[i];
BinTree bt = create(pre, mid, n);
mirror(bt);
lo(bt);
return 0;
}
2.2.1 该题的设计思路
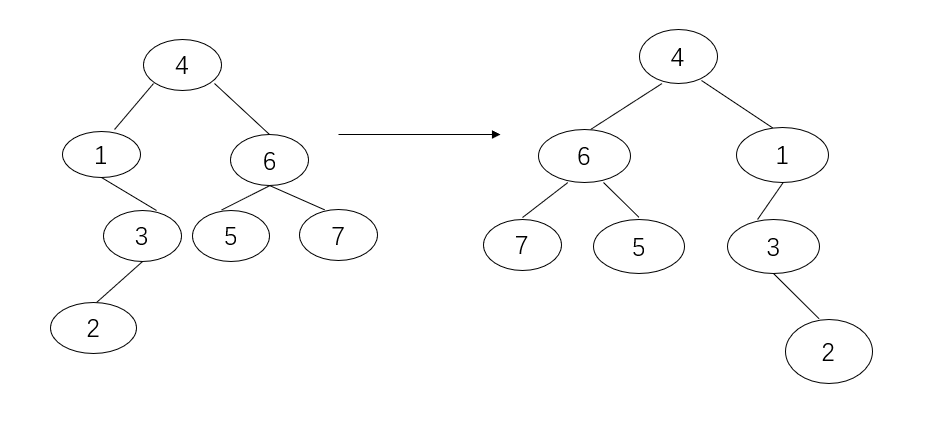
从镜面反转可以知道,反转后每一层的节点都会和原来的序列完全相反,因此或许可以不用写左右子树交换的代码,而是在层次遍历时做些手脚,每一层从最后一个节点开始遍历输出,也就是先右孩子在左孩子,这样一个小小的变动,瞬间就省去了很多麻烦。
2.2.2 该题的伪代码
create(pre[],mid[],len)函数
{
if(len为0)
return NULL
end if
给bt申请空间
for int i=0 to mid[i]!=pre[0] do i++
bt->left=creat(pre+1,mid,i)
bt->right=creat(pre+i+1,mid+i+1,len-i-1)
return bt
}
mirror(bt)函数
{
将bt的左右孩子互换
if(bt的左孩子不为空)
mirror(bt->left)
end if
if(bt的右孩子不为空)
mirror(bt->right)
end if
}
lo(bt)函数
{
定义树结点队列q
q.push(bt)
while(队列q不为空)
定义node=q.front()
q.pop()
输出node->data
if(node左孩子不为空)
q.push(node->left)
end if
if(node右孩子不为空)
q.push(node->right)
end if
end while
}
main函数
{
输入长度n
输入中序遍历结果mid[]
输入先序遍历结果pre[]
bt=creat(pre,mid,n)
mirror(bt)
lo(bt)
}
2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
- 优势:层次遍历输出的函数值得借鉴。在解题时,不要固性思维,可以多想想新的解题思路。可以通过学习别人的优秀代码,来扩宽自己的解题思路。有时候做题可能就会有意想不到的收获。
- 难点:如果层次遍历那里不能灵活转换的话,就会写左右子树交换的代码,加大题目的运行时间,反而更复杂
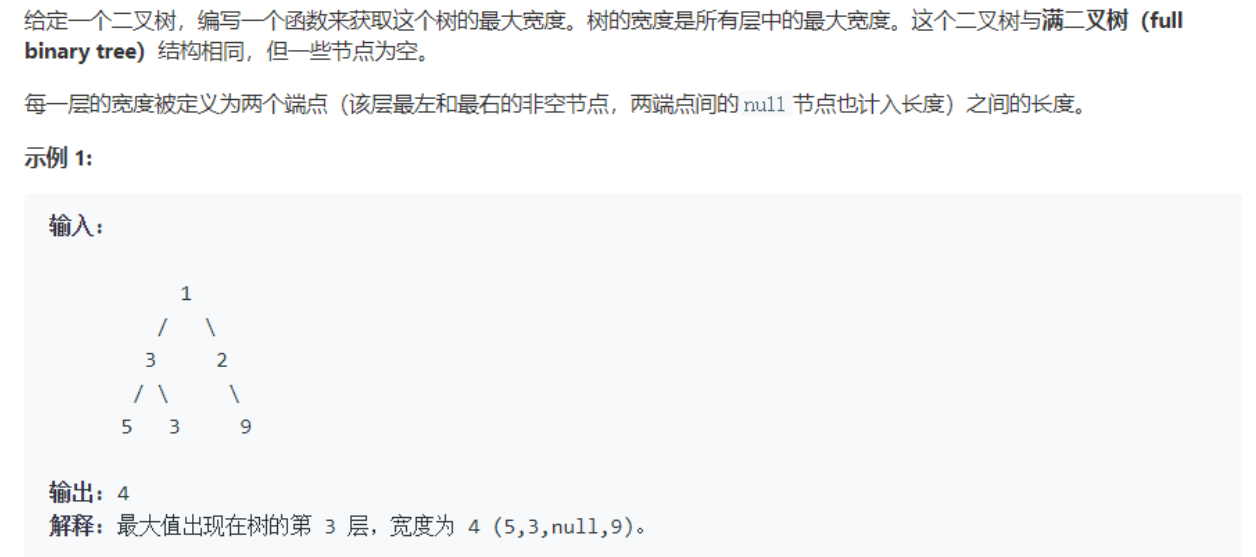
2.3 二叉树最大宽度
int widthOfBinaryTree(treenode*& root)
{
int ans = 0;
deque <Node> dque; //定义一个空的队列
Node tmp = NULL;
if (root == NULL)
return ans;
dque.push_back(root);
while (!dque.empty())
{
while (!dque.empty() && dque.front() == NULL)
dque.pop_front();
while (!dque.empty() && dque.back() == NULL)
dque.pop_back();
int n = dque.size();
if (n == 0)
break;
if (ans < n)
n = ans;
for (int i = 0; i < n; i++)
{
tmp = dque.front();
dque.pop_front();
dque.push_back(tmp == NULL ? NULL : tmp->left);
dque.push_back(tmp == NULL ? NULL : tmp->right);
}
}
return ans;
}
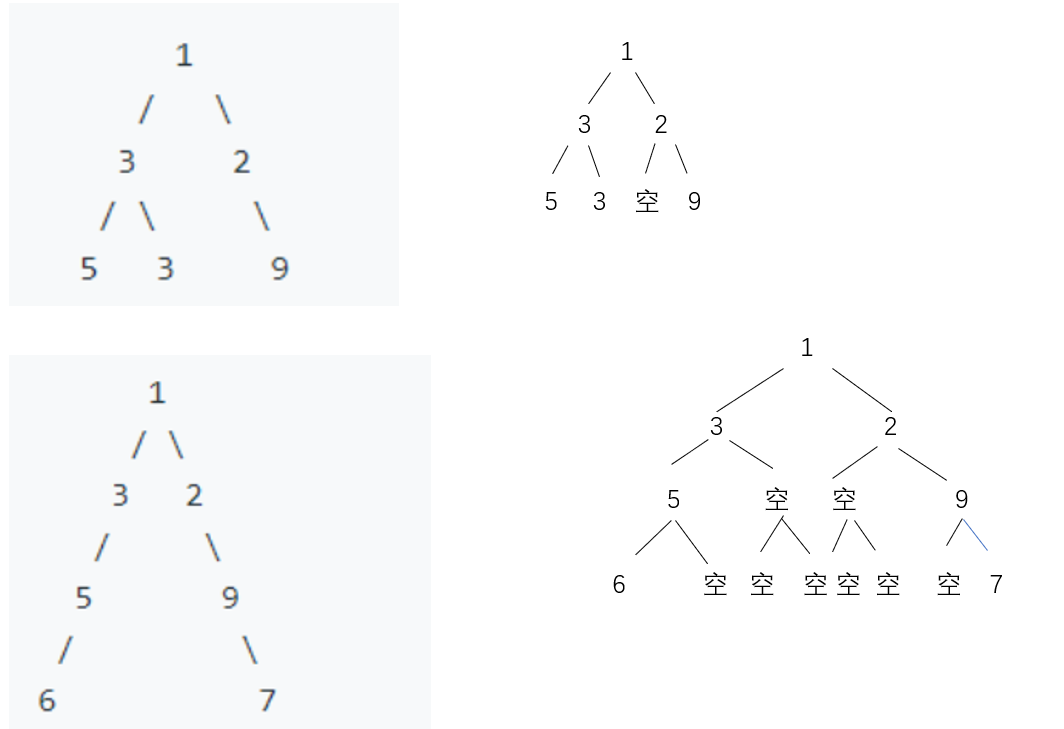
2.3.1 该题的设计思路
整体思路:采用双端队列,二叉树的层次遍历。每层遍历前,在队列中清除左右两边的null指针,再计算队列长度即为该层的宽度。
2.3.2 该题的伪代码
int widthOfBinaryTree(TreeNode* root)
定义整型变量ans用来记录层宽度,并初始化为0
定义一个双端队列dque
定义一个空指针tmp
if root ==NULL do
返回ans值
end if //即为空树的情况
否则root进队
while 队列不空 do
while 队列不空 and dque的队头为NULL do
将队头出队
end while
while 队列不空 and dque的对尾为NULL do
将队尾出队
end while
定义n存此时队列大小
将dque的size赋值给n
判断n和ans大小关系,将较大值赋给ans
if n=0 do /*即此时队列为空*/
break
end if
for i=0 to n do i++
取队列头赋值给tmp
队列头出队
tmp的左右结点进队 //注意:null指针的左右两个儿子均为null。
end for
end while
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
- 优势:运用了关于双端队列deque用法,即可以对队列的头尾都可以进行插入删除操作的队列。本题计算二叉树的最大宽度时要考虑到结点为空时此时依旧占有一个宽度的情况,所以计算时,是从队列最左边不是NULL位置开始到最右边不是NULL结束,即为该层的最大宽度;
- 难点:对空结点补NULL的时候是根据树的深度所判断的,这个地方就是这个题目的难点所在了,反而言之,求树的宽度就是求树的高度
2.4 二叉树

#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <unordered_map>
#include <map>
#include <algorithm>
using namespace std;
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
//以前序遍历创建二叉树
void CreateBiTree(TreeNode **T)//*T是指向BiTNode的指针
{
*T=new TreeNode(0);
if(*T==NULL)//如果*T还是指向NULL,表示内存分配失败,退出程序
exit(OVERFLOW);
char ch;
cin>>ch;
if(ch=='#')
*T=NULL;
else
{
(*T)->val=ch-'0';//*T指向的节点的data分配内容,即生成根节点
CreateBiTree(&((*T)->left));//创建&(*T)->lchild临时变量,传入CreateBiTree,构造左子树
CreateBiTree(&((*T)->right));//创建&(*T)->rchild临时变量,传入CreateBiTree,构造右子树
}
}
class Tree {
public:
int getDis(TreeNode* root)
{
// write code here
//第1步
map<int, pair<int, int>> parent;//标记每个子节点的父节点
queue<TreeNode*> que;//按照层序遍历处理每个节点
que.push(root);
parent[root->val] = make_pair(0, 0);//树根的双亲设置为(0,0)
int max = -65535;
int min = 65536;
int cnt = 0;//每处理一个节点计数加1
while (!que.empty())
{
//处理队列里的每个节点,每处理一个,计数加1。即cnt是目前处理的节点的序号(按层序遍历标序)。
TreeNode* temp = que.front();
cnt++;
//处理该节点的左右孩子
if (temp->left)//如果该节点有左孩子,标记左孩子,并且把左孩子入队列
{
parent[(temp->left)->val] = make_pair(temp->val, cnt);
que.push(temp->left);
}
if (temp->right)//如果该节点有右孩子,标记右孩子,并且把右孩子入队列
{
parent[(temp->right)->val] = make_pair(temp->val, cnt);
que.push(temp->right);
}
if (temp->left == NULL &&temp->right == NULL)//如果该节点是叶子节点,需要比较它和max和min的大小
{
if (temp->val > max)
max = temp->val;
if (temp->val < min)
min = temp->val;
}
que.pop();
}
//第2步
vector<int> v1;
vector<int> v2;
v1.push_back(min);
v2.push_back(max);
int move1 = min;
int move2 = max;
while(parent[move1].second > 0)//把min到树根的路径找出来
{
v1.push_back(parent[move1].first);
move1 = parent[move1].first;
}
while (parent[move2].second > 0)//把max到树根的路径找出来
{
v2.push_back(parent[move2].first);
move2 = parent[move2].first;
}
//反转一下方便查找公共串,第一个节点都是树根
reverse(v1.begin(), v1.end());
reverse(v2.begin(), v2.end());
int n = 0;
for (;v1[n] == v2[n];n++);//n是公共串的结尾
return (v1.size() + v2.size() - 2 * n);
}
};
//测试
int main()
{
TreeNode **pp;//定义指向BiTNode的二级指针pp
TreeNode *p;//定义指向BiTNode的指针p
pp=&p;//pp指向p
p=NULL;//初始化p指向NULL
CreateBiTree(pp);//传入指向p的地址,创建二叉树,输入5129###3##4#68##7##
Tree solution;
cout << solution.getDis(p);
return 0;
}
2.4.1 该题的设计思路
这道题的解题较为麻烦,分作两大步骤
1 标记每个节点的父节点,并且找出最大叶节点和最小叶节点
用map<int,pair<int,int>>标记每个子节点的父节点,first是子节点值,second是<父节点值,父节点位置>
用queue遍历二叉树的节点
依次把每个父节点的子节点push进队列,每取出一个节点处理,计数加1,然后处理取出节点的左右孩子进行标记
处理完之后,把取出的节点pop出去
2 计算两个叶节点的最短路径
分别找出两个叶节点到树根的路径,公共部分以前的路径相加即最短路径

2.4.2 该题的伪代码
getDis(TreeNode* root)函数
{
定义map<int,pair<int,int>> parent标记每个子节点的父节点
定义树结点队列que按照层序遍历处理每个结点
que.push(root)
将树根的双亲设置为(0,0)
定义 max=-65535
定义 min=65536
定义cnt=0用来统计处理的结点
while(队列不为空)
定义树结点temp=que.front()
cnt自增
if(temp->left不为空)
将左孩子的双亲设置为(temp->val,cnt)
que.push(temp->left)
end if
if(temp->right不为空)
将右孩子的双亲设置为(temp->val,cnt)
que.push(temp->right)
end if
if(temp左右孩子都为空)
将max,min重置
end if
que.pop()
定义双端队列v1,v2
v1.push_back(min)
v2.push_back(max)
定义move1=min,move2=max
while(parent[move1].second 大于 0)
v1.push_back(parent[move1].first);
将move1重置为parent[move1].first
end while
while(parent[move2].second 大于 0)
v2.push_back(parent[move2].first);
将move2重置为parent[move2].first
end while
将v1,v2反转
for int n=0 to v1[n]==v2[n] do n++
return (v1.size() + v2.size() - 2 * n)
}
2.4.3 运行结果

2.4.4分析该题目解题优势及难点
- 优势:没想到孰能解决的问题这么多,这道题看起来不是很难,只要找出权值最大的节点和权值最小的叶节点,然后在计算他们之间的距离。但是实际操作起来的话,首先找权值的问题是要先遍历一遍整棵树,把权值记录下来,然后进行比较找出两个节点,然后在进行遍历,便利的同时记录下来路径,存放好路径之后再使用一个函数进行计算路径。这道题用了很多的书的操作,创建左右子树,遍历子树,然后就是栈和队列的操作,很值得学习和深思。
- 难点:这道题注意是最大的叶子节点到最小的叶子节点的距离。叶子节点是没有左右孩子的节点。首先求出二叉树中所有从根节点到叶子节点的路径,然后找到权值最大的叶子节点和权值最小的叶子节点所在的路径所在的路径的编号。该问题可以转换为两个节点到最低公共祖先的距离问题。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号