数字图像处理---图像分割

图像分割

概述

图像分析

  • 概念：对图像中感兴趣的目标进行检测和测量，以获得它们的客观信息，从而建立对图像的描述
  • 步骤：
    1. 图像分割
    2. 特征识别
    3. 对象分类
    4. 建立联系

概述图像分割

  • 概念：将图像划分为互不重叠的区域并提取感兴趣目标的技术
  • 基本策略：
    • 基于灰度值的两个基本特性：不连续性和相似性
    • 通过检测不连续性先找边，后确定区域
    • 通过检测相似性，在一定阈值下找到灰度值相似区域，区域外轮廓即为对象边界
  • 方法
    • 基于边缘的分割方法：先提取区域边界，再确定边界限定区域
    • 区域分割：确定每个像素归属区域，从而形成区域图
    • 区域生长：将属性接近的连通像素聚集成区域
    • 分裂-合并分割：即存在图像划分，也存在图像合并

边缘检测算子---边缘分割法

边缘

  • 定义：图像中像素灰度有阶跃变化或屋顶变化的像素的集合
  • 分类：
    • 阶跃状
    • 屋顶状
  • 特点：
    • 属于高频信号区域
    • 往往为闭合连线
  • 边缘检测流程

    \[滤波 \Rightarrow 增强 \Rightarrow 检测 \Rightarrow 定位 \]

边缘检测算子

  • 基本思想：计算局部微分算子
  • 一阶微分：用梯度算子进行运算
    • 特点：
      • 对于阶跃状变化会出现极大值（两侧都是正值，中间最大）
      • 对于屋顶状变化会过零点（两侧符号相反）
      • 不变部分为0
    • 用途：检测图像中边的存在
    • 注意事项：由于结果图中存在负值，因此需要处理后使用
    • 处理方法：
      • 取绝对值
      • 加最小值
      • 阈值法
  • 二阶微分：通过拉普拉斯算子计算
    • 特点：
      • 对于阶跃状变化会过零点（两侧符号相反）
      • 对于屋顶状变化会出现负极大值（两侧都是正值，中间最小）
      • 不变部分为0
    • 用途：检测图像中边的存在

常用边缘检测算子

  • 梯度算子
  • Roberts算子
  • Prewitt算子
  • Sobel算子
  • Kirsch算子
  • Laplacian算子
  • Marr算子

交叉方向一阶锐化

  • 问题：锐化处理结果对具有矩形特征的物体的边缘提取较为有效，但是对于不规则形状的边缘提取，则存在信息上的缺损
  • 解决思想：利用无方向的锐化算法

交叉微分算子

交叉Roberts算子
  • 公式：

\[f'_x=|f(x+1,y+1)-f(x,y)| \]

\[f'_y=|f(x+1,y)-f(x,y+1)| \]

  • 模板:

\[f'_x= \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} ,f'_y= \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \]

  • 特点：算法简单,对噪声敏感，效果较梯度算子较好
交叉Prewitt算子
  • 模板:

\[d'_x= \begin{bmatrix} 0 & 1 & 1 \\ -1 & 0 & 1 \\ -1 & -1 & 0 \end{bmatrix} ,d'_y= \begin{bmatrix} -1 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix} \]

  • 特点：与Sobel相比有一定抗干扰性，图像效果较干净
交叉Sobel算子
  • 模板:

\[d'_x= \begin{bmatrix} 0 & 1 & 2 \\ -1 & 0 & 1 \\ -2 & -1 & 0 \end{bmatrix} ,d'_y= \begin{bmatrix} -2 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 2 \end{bmatrix} \]

  • 特点：锐化的边缘信息较强
kirsch 算子(方向算子)

  • 模板：

    kirsch 算子

  • 特点

    • 在计算边缘强度的同时可以得到边缘方向
    • 各方向间的夹角为45°

  • 分析

    • 取其中最大的值作为边缘强度，与之对应的方向作为边缘方向
    • 若取最大值绝对值，则仅需要前四个模板即可
Nevitia算子

  • 模板：

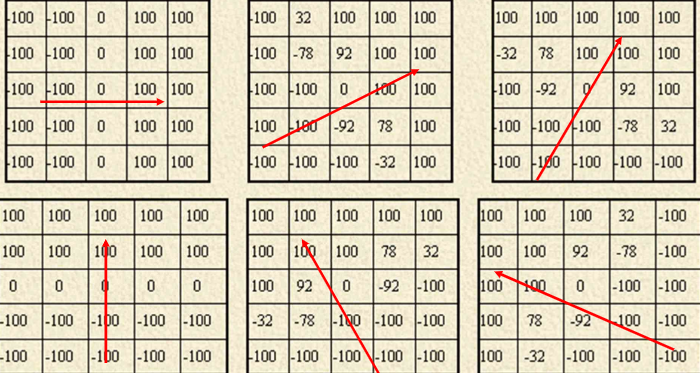
    Nevitia算子

  • 特点:各方向间的夹角为30°

Laplacian算子

同图像增强中的Laplacian算子

  • 优点：
    • 各向同性、线性和位移不变
    • 对细线和孤立点检测效果较好
  • 缺点
    • 对噪声敏感，有双倍加强作用
    • 不能检测出边缘方向
    • 常产生双像素边缘

使用之前需要对图像进行平滑

Marr算子

在Laplacian算子基础上发展而来

平滑函数采用高斯正态分布函数

\[h(x,y)= e ^{-\frac{x^2+y^2}{2 \sigma^2}} \]

\[\sigma 为方差 \]

用\(h(x,y)\)对图像\(f(x,y)\)平滑克表示为

\[g(x,y) = h(x,y) * f(x,y) \]

*代表卷积

令r表示从原点出发的径向距离，即\(r^2=x^2+y^2\)

利用高斯-拉普拉斯滤波器（LOG滤波器）

\[\bigtriangledown ^2h = (\frac{r^2-2\sigma^2}{\sigma^4})e^{-\frac{r^2}{2\sigma^2}} \]

即可利用二阶导数算子过零点的性质，确定图像中阶跃边缘的位置

在该算子中\(\sigma\)越小边缘位置精度越高，边缘细节变化越多；\(\sigma\)越大平滑作用越大，但是细节损失越大，边缘点定位精度越低

  • 过程
    1. 通过二维高斯函数对图像进行卷积降噪
    2. 用二阶导数差分算子计算图像强度的二阶导数
    3. 利用二阶导数算子过零点的性质，确定图像中阶跃边缘的位置
  • 优点：能快速得到一个闭合的轮廓
  • 缺点：对噪声敏感

Canny边缘检测算子

  • 最优边缘检测算子应有的指标
    • 低误判率
    • 高定位精度
    • 抑制虚假边缘
  • 过程：
    1. 计算图像梯度
    2. 梯度非极大值抑制
    3. 双阈值提取边缘点
  • 计算图像梯度
    • 高斯函数的一阶导数
    • 模板：

    \[ \begin{bmatrix} -1 & 1 \\ -1 & 1 \end{bmatrix} ,\begin{bmatrix} -1 & -1 \\ 1 & 1 \end{bmatrix} \]

  • 非极大值抑制 NMS
    • 思想：梯度幅值图像M(x,y)，仅保留梯度方向上的极大值点
    • 过程
      • 初始化N(x,y)=M(x,y)
      • 对每一点在梯度方向和反梯度方向各找n个点，若M(x,y)非最大值，则置零，否则保持不变
  • 对NMS结果二值化（双阈值提取边缘点）
    • 使用两个阈值\(T_1,T_2:T_2>>T_1\)
      • 由\(T_1\)得到\(E_1(x,y)\),低阈值边缘图：更大的误检率
      • 由\(T_2\)得到\(E_2(x,y)\),高阈值边缘图：更可靠
    • 边缘连接
      • 初始化\(E(x,y)\)=\(E_2(x,y)\)
      • 对\(E(x,y)\)中的每个点在\(E_1(x,y)\)中寻找延长部分进行连接
      • 输出\(E(x,y)\)

Canny边缘检测算子步骤

  1. 高斯滤波器平滑
  2. 一阶偏导计算梯度幅值与方向
  3. 对梯度幅值进行非极大值抑制
  4. 双阈值算法检测连接边缘

Canny边缘检测算子优点

  • 参数较小
  • 计算效率高
  • 得到边缘连续完整

双阈值选择\(T_{Low}=T_{HIGH}*0.4\)

曲面拟合法

  • 出发点：基于差分检测图像边缘的算子往往对噪声敏感
  • 四点拟合灰度表面法
    • 用一平面\(p(x,y)=ax+by+c\)来拟合四邻域像素灰度值
    • 定义均方差为

      \[\varepsilon = \sum [p(x,y)-f(x,y)]^2 \]

    • 模板

      \[a=\frac{1}{2}\begin{bmatrix} -1 & -1 \\ 1 & 1 \end{bmatrix}, b = \frac{1}{2}\begin{bmatrix} -1 & 1 \\ -1 & 1 \end{bmatrix} \]

    • 特点：
      • 先平均后求差分，对噪声由抑制作用

边缘跟踪

  • 出发点：
    • 噪声
    • 边检测需要归整边缘像素
  • 概念：将检测的边缘点连接成线
  • 过程：
    • 边缘提取
    • 连接成线
  • 方法
    • 光栅扫描跟踪法
    • 全向跟踪法

光栅扫描跟踪法

  • 概念：采用电视光栅行扫描顺序，结合门限检测，对遇到的像素进行分析并确定其是否是边缘的跟踪方法
  • 具体步骤：
    • 确定检测阈值d（较高）
    • 超过d的点作为对象点
    • 确定跟踪阈值t（较低）
    • 确定跟踪邻域
    • 扫描下一行，跟踪邻域内灰度差小于t的，接受为对象点
    • 若没有对象点，则该曲线跟踪结束
    • 重新从下一行开始利用d寻找对象点并进行跟踪
    • 扫描结束后跟踪结束
  • 特征可以不是灰度级
  • 跟踪准则根据具体问题灵活运用
  • 最好再进行一次其他方向的跟踪

全向跟踪

Hough变化检测法

  • 问题：如何连接边界点集
  • 基本思想
    • 利用xoy直角坐标系直线\(y=ax+b\),待求
    • 极坐标系内点\((\rho,\theta)\),已知
    • 求点到线的变化\(\rho = x cos \theta + y sin \theta\)
  • 原理:过每个点的直线系分别对应极坐标系上的一条正弦曲线，如正弦曲线存在共同交点\((\rho',\theta')\),则必定在平面上共线
  • 实现：
    • 使用交点累积器或直方图，寻找相交线段最多的参数空间的点，再寻找对应的直线线段
  • 特点：
  • 对\(\rho、\theta\)量化过粗会导致直线参数不精确，过细会导致计算量增加
  • 获得直线抗噪能力强
  • 可以用来检测直线

阈值分割法

  • 基本思想：通过阈值T生成二值图，在四邻域中有背景的像素就是边界像素
  • 特点：
    • 适用于物体与背景有强对比的情况下，且物体或背景的灰度较单一
    • 可以先求背景再求物体
    • 可以得到封闭且连通区域的边界
  • 通过交互获得阈值
  • 通过直方图得到阈值
    • 基本思想：边界上的点灰度值出现次数较少
    • 方法：选取直方图谷底的最小灰度值作为阈值
    • 缺点：会受到噪声干扰
    • 改进：
      • 取两个峰值之间的某个固定位置
      • 降噪

简单图像的阈值分割

  • 判断分析法
  • 最佳熵自动阈值法

复杂图像的阈值分割

  • 步骤
    • 自动平滑直方图
    • 确定区域类数
    • 自动搜索多个阈值

特征空间聚类

k均值聚类

  • 步骤
    • 任意选取K个初始聚类中心值
    • 使用最小距离判别，将新读入的像素分至K类
    • 重新计算中心值，等于一类元素的平均值
    • 重新聚类直至新旧差异不大

区域增长

通过像素集合的区域增长

  • 实现：
    • 根据应用选取种子
    • 选择描述符
    • 种子根据描述符扩张直至没有新的节点加入集合

简单区域扩张法

以未划分点与起点灰度差小于阈值T作为描述符

优缺点：

  1. 不好确定阈值
  2. 无法分割缓慢变化边界

质心区域增长法

以未划分点与区域平均灰度值差小于阈值T作为描述符

分裂合并法

实现：

  1. 对于灰度级不同的区域划分为四个子区域
  2. 若相邻子区域所有像素灰度级相同，则合并
  3. 反复进行直至不再进行新的分裂合并操作
posted @ 2020-12-12 18:03  springfield_psk  阅读(997)  评论(0)  编辑  收藏  举报