opengl算法学习---三维观察

概述

三维场景观察遵循二维观察中所使用的一般方法，即首先在建模坐标或直接在世界坐标里的对象定义中创建世界坐标场景，然后建立观察坐标参照系并将对象描述从世界坐标变换到观察坐标，最后将观察坐标描述变换到设备坐标。

不同同于二维观察，三维观察在变换到设备坐标之前，需要投影程序把对象描述变换到观察平面上，三维观察操作包含更多的空间参数，对已选择的视图，必须识别场景的可见部分，对于场景的真实绘制，则必须使用相关的表面绘制算法。

三维观察流水线

三维对象在局部的建模坐标系（MC）中完成后，需要组装到统一的世界坐标系（WC）中搭建场景模型，并再将场景描述转换到选择的观察坐标系(VC)。观察坐标系定义了观察参数，包括投影平面(观察平面)的位置和方向，投影平面可视为照相机胶片平面。

在投影平面上定义为照相机镜头对应的二维裁剪窗口,并建立三维裁剪区域。该裁剪区域称为视景体(view volume )，其形状和大小依赖于裁剪窗口的尺寸、投影方式和所选的观察方向的边界位置。

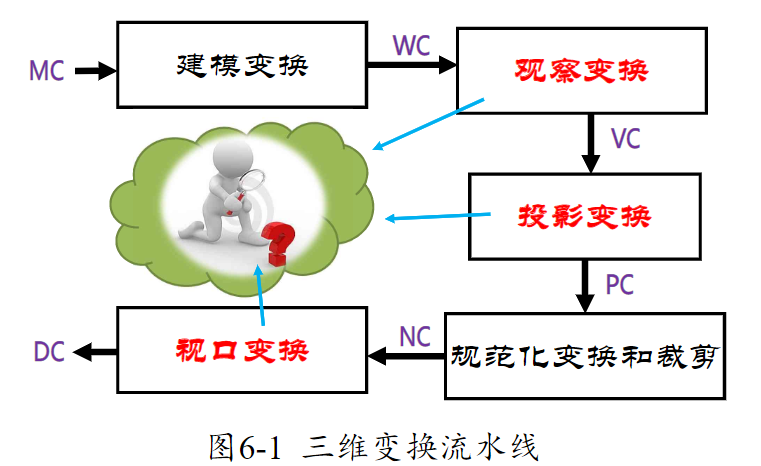
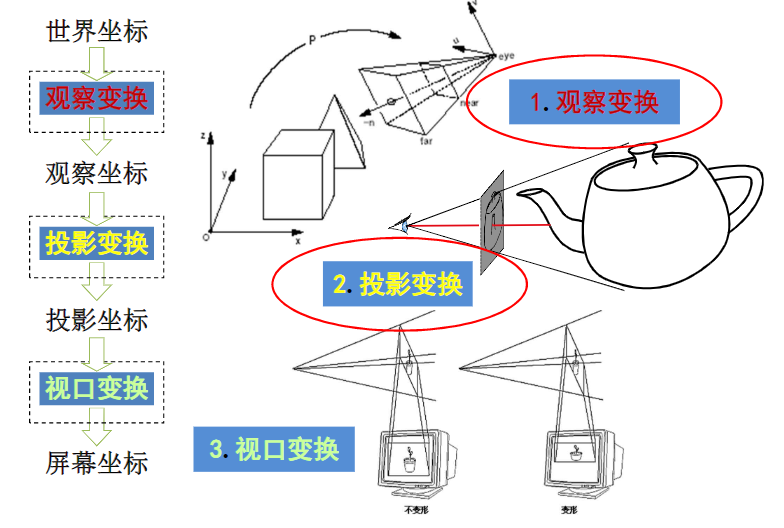
观察变换

三维观察变换系参数

观察变换指从世界坐标空间到观察坐标系空间的变换，也称视点变换。在观察坐标空间中，某些操作更方便，通常 观察坐标系的原点模拟视点或摄像机的位置，Z轴与观察方向共线，它可被放置在世界坐标系中的任意位置并指向
任意方向，还可以随意旋转，这样能够很好地模拟人眼或摄像机对场景的各类观察情形

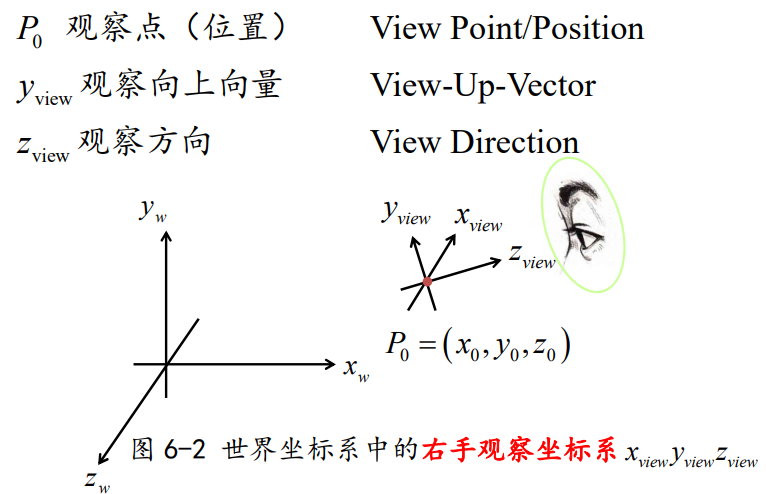
(1)观察平面法向量(View Plane Normal Vector)
因为观察方向通常沿着z_view轴，因此观察平面(View Plane)有时也称为投影平面(Projection Plane)。
观察平面沿z_view轴方向移动,设与z_view轴交点为z_vp,该参数表示为从观察原点沿观察方向到观察平面的距离，常为负。人机交互中,投影平面满足如下过视心参考点\(\bar{o}=(x_{0},y_{0},z_{0})\)且与法向量\(N=(x_{n},y_{n},z_{n})\)相垂直的平面方程:

\[x_{n}(x-x_{0})+y_{n}(y-y_{0})+z_{n}(z-z_{0})=0 \]

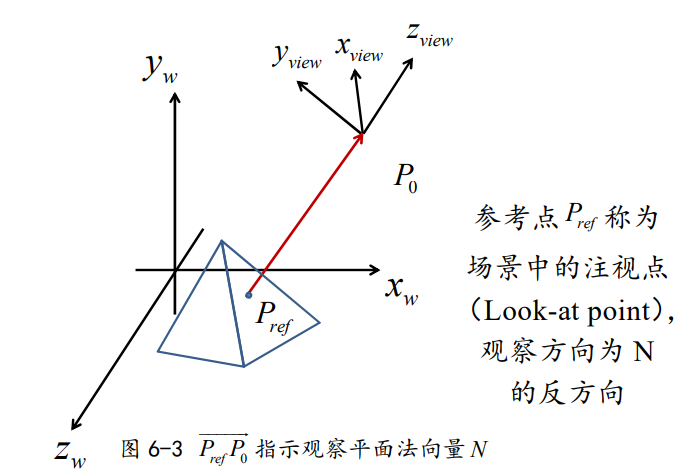
(2)观察向上向量
选定观察平面法向量N后，可接着选择观察向上向量V,该向量用来确定y_view轴正向。

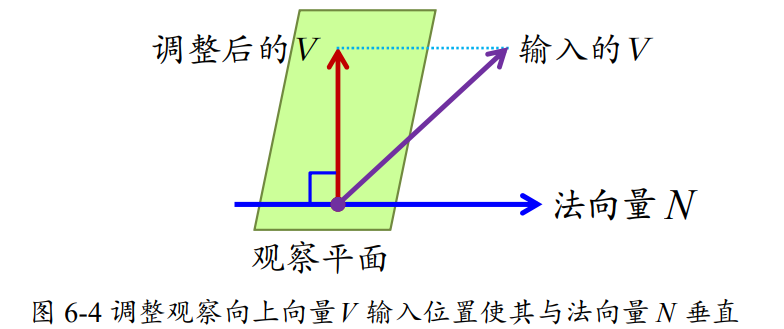
(3)uvn观察坐标系统（右手观察坐标系统）
单位化

\[z_{view}=n=\frac{N}{|N|}=(n_{x},n_{y},n_{z}) \]

\[x_{view}=u=\frac{V \times N}{|V \times N|}=(u_{x},u_{y},u_{z}) \]

\[y_{view}=v=n \times u =(v_{x},v_{y},v_{z}) \]

在交互式应用中，法向量N是一个经常变动的观察参数。当然，在修改N的方向时，也要修改其他轴向量从而维护右手观察坐标系统。
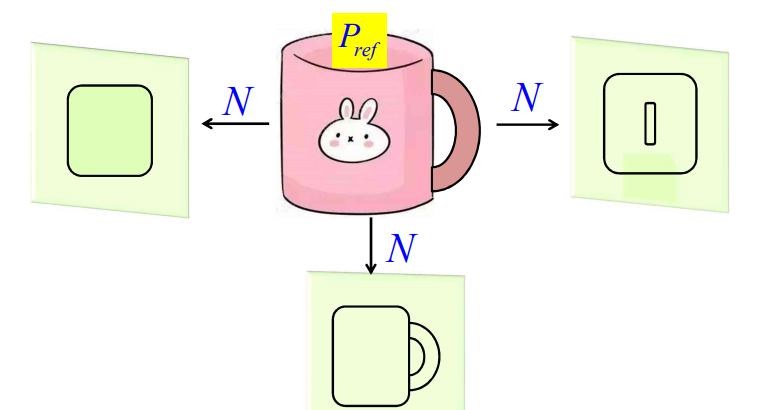
(1)通过固定的方向、改变观察参考点位置而生成移镜效果

(2)以固定观察参考点对某一特定场景从不同方向进行观察.

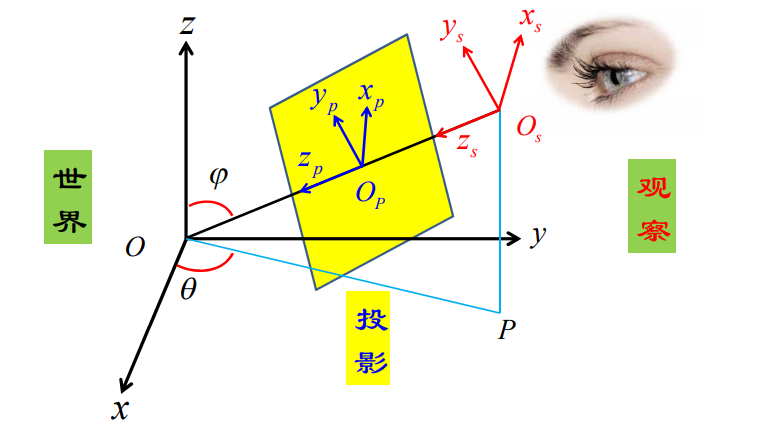
世界坐标系到观察坐标系的变换

1)世界坐标系
视点直角坐标\(O_{s}(a,b,c)，|OO_{s}|=R\)，夹角φ和θ如图所示。视点的球面坐标与直角坐标的关系为

\[\left\{\begin{matrix} a=R \cdot sin \varphi \cdot cos \theta \\ b=R \cdot sin \varphi \cdot sin \theta \\ c=R \cdot cos \varphi \end{matrix}\right. \]

2)观察坐标系
此处的观察坐标系采用左手系，坐标原点即为视点\(O_{s}\); z_s 轴沿着视线方
向0_s0，视线的正上方为y_s轴，视线的正右方为x_s轴。

3)投影平面坐标系
投影平面坐标系也是左手系，坐标原点O_p,位于视心。投影平面坐标系的x_p轴、y_p轴与观察坐标系的x_s轴、y_s轴方向一致，z_p轴与z_s轴重合，也就是说投影平面垂直于视线。

观察变换坐标系
1)把世界坐标系原点O(0,0,0)平移到观察坐标系原点O_s(a,b,c)，形成新坐标系O₁x₁y₁z₁，则P(x,y,z)在新坐标系O₁x₁y₁z₁下的新坐标为P₁(x₁,y₁,z₁)。
即进行一次平移变换\(P_{1}=T_{1}P\)

\[T_{1}= \begin{bmatrix} 1 & 0 & 0 & -a \\ 0 & 1 & 0 &-b \\ 0 & 0 & 1 & -c \\ 0 & 0& 0 &1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & -R \cdot sin \varphi \cdot cos \theta \\ 0 & 1 & 0 & -R \cdot sin \varphi \cdot sin \theta \\ 0 & 0 & 1 & -R \cdot cos \varphi \\ 0 & 0& 0 &1 \end{bmatrix} \]

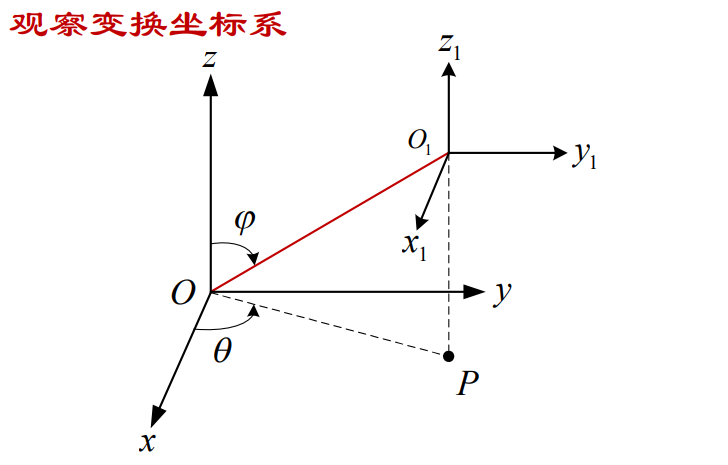
2)坐标系O₁x₁y₁z₁绕z₁轴顺时针旋转90°-θ角，使y₁轴位于O₁O_pO平面内，形成新坐标系O₂x₂y₂z₂(由于变换对象为坐标系，旋转参数需取反)
即进行一次旋转变换\(P_{2}=R_{2}P_{1}\)

\[R_{2}= \begin{bmatrix} cos (\pi / 2 - \theta) & -sin (\pi / 2 - \theta) & 0 & 0 \\ sin (\pi / 2 - \theta) & cos (\pi / 2 - \theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} sin \theta & -cos \theta & 0 & 0 \\ cos \theta & sin \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

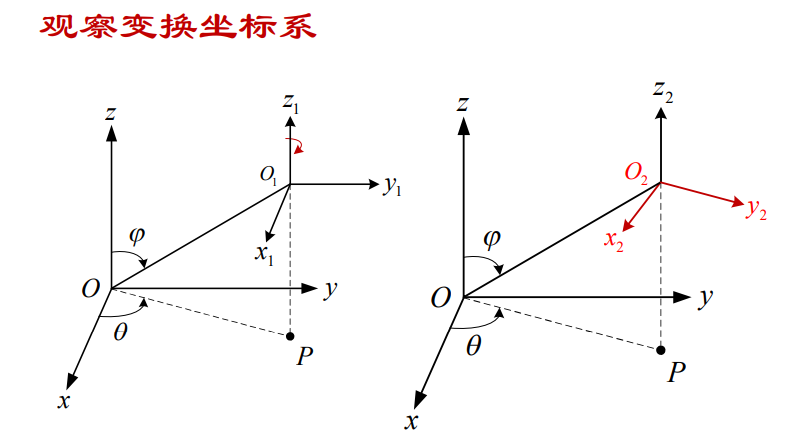
3)坐标系O₂x₂y₂z₂绕x₂轴逆时针旋转$180° - \varphi \(角，使z~2~轴沿视线方向，形成新坐标系O~3~x~3~y~3~z~3~(由于变换对象为坐标系，旋转参数需取反) 即进行一次旋转变换\)P_{3}=R_{3}P_{2}$

\[R_{3}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos (\pi - \varphi) & sin (\pi - \varphi) & 0 \\ 0 & -sin (\pi - \varphi) & cos (\pi - \varphi) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & -cos (\varphi) & sin (\varphi) & 0 \\ 0 & -sin (\varphi) & -cos (\varphi) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}= \]

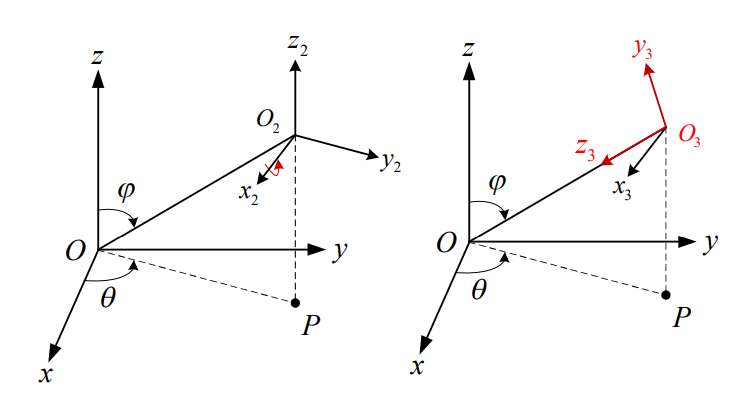
4)由于世界坐标系是右手坐标系，观察坐标系是左手坐标系，因此两者之间还需要通过一次对称变换才能完全重合。故将轴x₃作关于y₃O₃z₃面的对称变换，得到最终的观察坐标系O_vx_vy_vz_v。

即进行一次对称变换\(P_{4}=M_{4}P_{3}\)

\[M_{4}= \begin{bmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

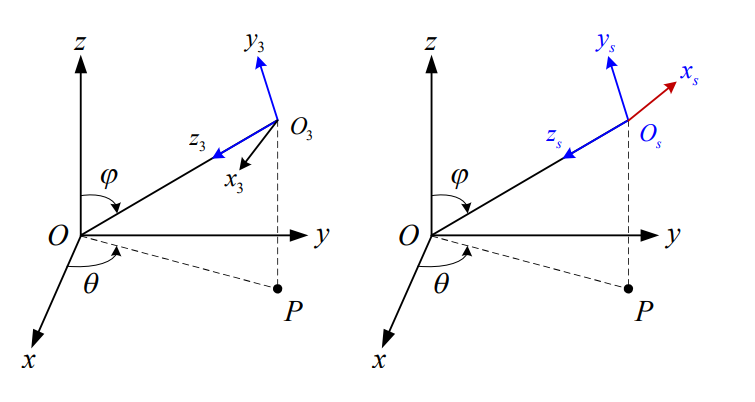
复合变换矩阵

\[M=M_{4}R_{3}R_{2}T_{1}= \begin{bmatrix} -sin \theta & cos \theta & 0 & 0 \\ -cos \theta cos \varphi & -sin \theta cos \varphi & sin \varphi & 0 \\ -cos \theta sin \varphi & -sin \theta sin \varphi & -cos \varphi & R \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

所以
世界坐标系到观察坐标系变换为

\[\begin{pmatrix} {x}'&{y}'&{z}'&1 \end{pmatrix} ^{T} = M \cdot \begin{pmatrix} x& y & z & 1\end{pmatrix}^{T} \]

投影变换

世界坐标系下的对象描述变换到观察坐标系后，这些客观物体或形体等对象描述仍然是三维的,而这些对象的图形显示与图形输出最终都只能在二维平面内实现。因此采用投影的方法，把三维物体变为二维图形表示，这个过程称为投影变换。

平面投影过程:
首先在三维空间中选择一个点为投影中心(或称投影参考点)，再定义一个不经过投影中心的投影面，即前面提及的观察平面,连接投影中心与三维物体(线段AB)的线,称为投影线,投影线或其延长线将与投影面相交，在投影面上形成物体的像，这个像称为三维物体在二维投影面.上的投影。实际上，投影中心相当于人的视点，投影线则相当于视线。

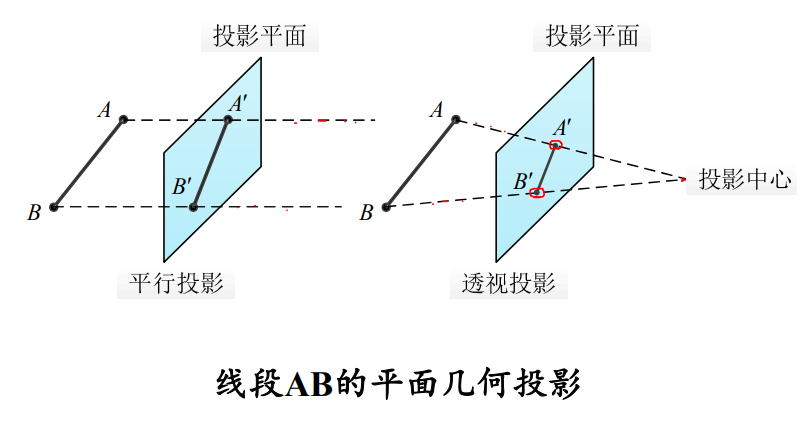
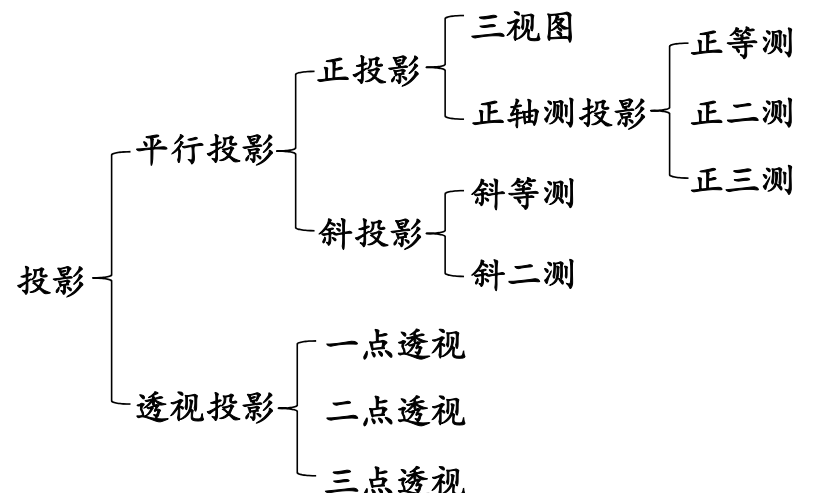
平行投影

正投影

对象描述沿与投影平面法向量平行的方向到投影平面上的变换称为正投影或正交投影。正投影常常用来生成对象的三视图和正轴测视图，当观察平面与某一坐标轴垂直时，得到的投影为三视图，否则，得到的投影为正轴测视图。

点的正投影
点在单个投影面上的投影不能确定点的空间位置
需要通过多面投影，如三视图

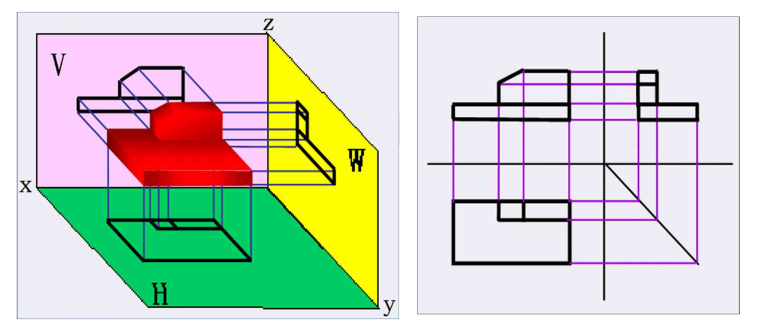
三视图

先投影后展开
主视图
将三维形体向xoz面（V面）作正投影得到
投影矩阵为

\[\begin{bmatrix} {x}' & {y}' & {z}' & 1 \end{bmatrix} = \begin{bmatrix} x & y & z & 1 \end{bmatrix} \begin{bmatrix} 1 &0 & 0 & 0 \\ 0 &0 & 0 & 0 \\ 0 &0 & 1 & 0 \\ 0 &0 & 0 & 1 \\ \end{bmatrix} \]

俯视图
将三维形体向xoy面（H面）作正投影再旋转得到
1）xoy面（H面）作正投影 2） 使H面绕x轴转-90°
投影矩阵为

\[\begin{bmatrix} {x}' & {y}' & {z}' & 1 \end{bmatrix} = \begin{bmatrix} x & y & z & 1 \end{bmatrix} \begin{bmatrix} 1 &0 & 0 & 0 \\ 0 &1 & 0 & 0 \\ 0 &0 & 0 & 0 \\ 0 &0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 &0 & 0 & 0 \\ 0 & cos(- \pi /2) & sin (- \pi /2) & 0 \\ 0 & -sin(- \pi /2) & cos (- \pi /2) & 0 \\ 0 &0 & 0 & 1 \\ \end{bmatrix} \]

侧视图
先将物体向YOZ平面作正投影（即坐标x=0），然后绕Z轴逆时针旋转90度，使其与V面共面

\[\begin{bmatrix} {x}' & {y}' & {z}' & 1 \end{bmatrix} = \begin{bmatrix} x & y & z & 1 \end{bmatrix} \begin{bmatrix} 0 &0 & 0 & 0 \\ 0 &1 & 0 & 0 \\ 0 &0 & 1 & 0 \\ 0 &0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} cos(- \pi /2) &sin (- \pi /2) & 0 & 0 \\ -sin(- \pi /2) & cos (- \pi /2) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 &0 & 0 & 1 \\ \end{bmatrix} \]

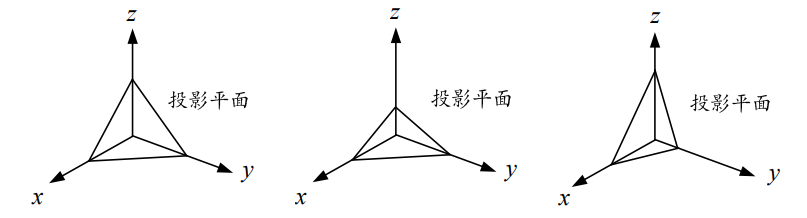
正轴测视图

当观察平面与三个坐标轴之间的夹角都相等时为正等测;当观察平面与两个坐标轴之间的夹角相等时为正二侧;当观察平面与3个坐标轴之间的夹角都不相等时为正三测。

斜投影

当投影路径与观察平面不垂直时，该映射称为斜平行投影，简称斜投影。


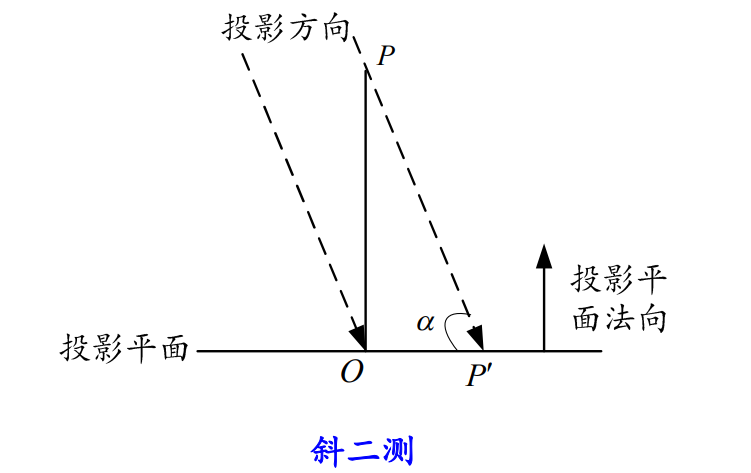
斜平行投影常使用两个角度描述

透视投影

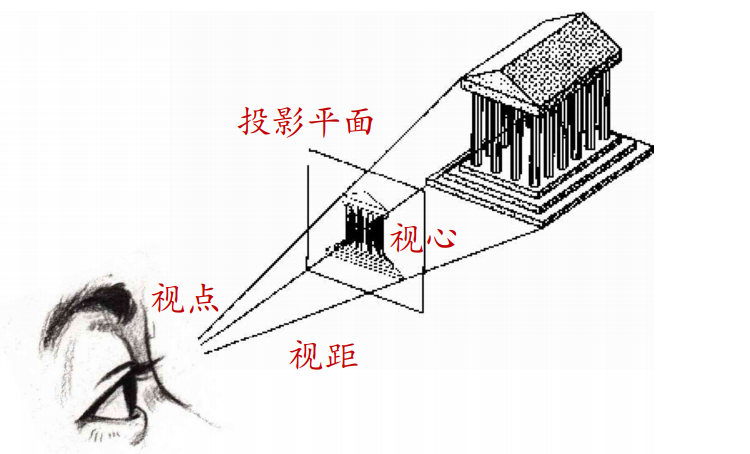
与平行投影相比，透视投影的特点是所有的投影线都从空间一点投射，离视点近的物体投影大，离视点远的物体投影小，小到极点成为灭点。生活中照相机拍摄的照片，画家的写生画等均是透视投影的例子。透视投影模拟了人的眼睛观察物体的过程，符合人类的视觉习惯，所以在真实感图形中得到广泛应用。

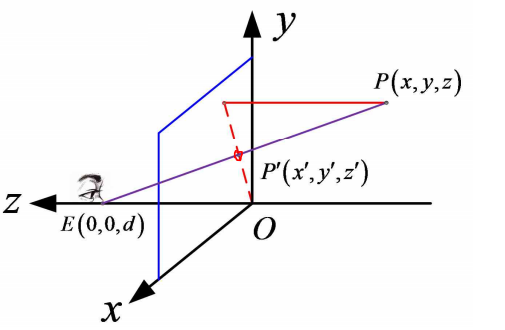
为推导点的透视投影规律,首先根据问题需要在观察坐标系中建立投影坐标系。设视距为d，将观察坐标系沿z轴
向其负方向平移距离d，则投影面与平移后所得的Oxyz坐标系直接设为投影坐标系，其中，视点E(0,0,d)，设空间任意一点为P(x,y,z),视线EP与投影面的交点为P',称为点P的透视投影。

令t为参数，可得视线EP的直线参数方程为

\[\left\{\begin{matrix} X=0+(x-0)t \\ Y=0+(y-0)t \\ Z=d+(z-d)t \end{matrix}\right. \]

视线EP与投影平面Z=0相交时的参数t=d/(d-z),带入直线参数方程，得

\[\left\{\begin{matrix} {x}'=xd/(d-z) \\ {y}'=yd/(d-z) \\ {z}'=0 \end{matrix}\right. \]

上述结果也可以通过相似三角形来推导得出，用齐次坐标写成矩阵形式为

\[{P}'= \begin{bmatrix} {x}' \\ {y}' \\ {z}' \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{x}{1- \frac{z}{d}} \\ \frac{y}{1- \frac{z}{d}} \\0 \\ 1 \end{bmatrix} =\frac{1}{1- \frac{z}{d}} \begin{bmatrix} 1 & 0 & 0& 0\\ 0 &1 & 0& 0 \\ 0 & 0 &0 &0 \\ 0 & 0 & -\frac{1}{d} & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = MP \]

根据点的透视投影变换公式，不难发现透视投影后z'=0,导致P点离视点的距离(即深度)信息无法计算，这将导致
后续无法进行隐藏面消除。

此处，P点的实际深度为\(\sqrt{x^{2}+y^{2}+(z-d)^{2}}\)
实际应用中，通常在投影后对投影点增加一个伪深度值，提供对P点深度的适当度量，从而实现消隐。

对消除隐藏面而言，真正需要是一种距离视点的度量方法,使得当两个点投影到投影面时能够判别出哪个点更靠近视点从而使其可见。显然，深度值与点的纵坐标z负相关。因此可将-z作为该点伪深度值。

考虑到伪深度值与z的线性关系和变换表达式的一致性可采用如下保留z坐标的变换式

\[\left\{\begin{matrix} {x}'=x/(1- \frac{z}{d}) \\ {y}'=y/(1- \frac{z}{d}) \\ {z}'=z/(1- \frac{z}{d}) \end{matrix}\right. \]

用齐次坐标写成矩阵形式为

\[{P}'= \begin{bmatrix} {x}' \\ {y}' \\ {z}' \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{x}{1- \frac{z}{d}} \\ \frac{y}{1- \frac{z}{d}} \\ \frac{z}{1- \frac{z}{d}} \\ 1 \end{bmatrix} =\frac{1}{1- \frac{z}{d}} \begin{bmatrix} 1 & 0 & 0& 0\\ 0 &1 & 0& 0 \\ 0 & 0 &1 &0 \\ 0 & 0 & -\frac{1}{d} & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = TP \]

矩阵T称之为透视变换矩阵，把一个三维点P变换为另外一个三维点P'

其中，P'点称为P点的透视。变换后P'点坐标的前两个分量即为P点的投影坐标，而第三个分量可用于深度测试和隐
藏面消除。

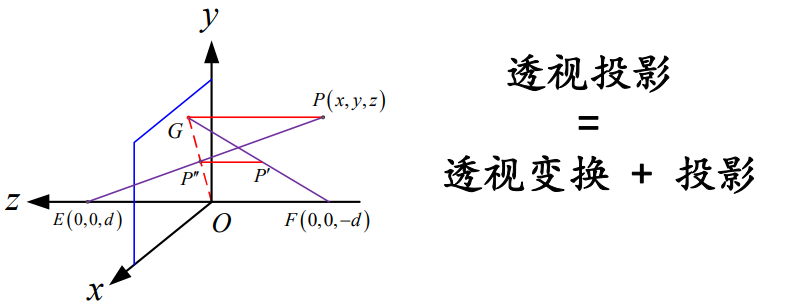
当z=0时，点的透视与原有点重合，也即投影面上点的透视就是其自身;
当z→$\infty $时，z'→-d，同时有P'(x,y,z)→F(0,0,-d),即视线上无穷远处的点，其透视趋近于点F(0,0,-d)，称之为灭点。

主轴及平行于该主轴方向的平行线在屏幕上投影形成的灭点称为主灭点。

一点透视(平行透视)

世界坐标系某一主轴垂直于投影平面
透视图只有一个主灭点

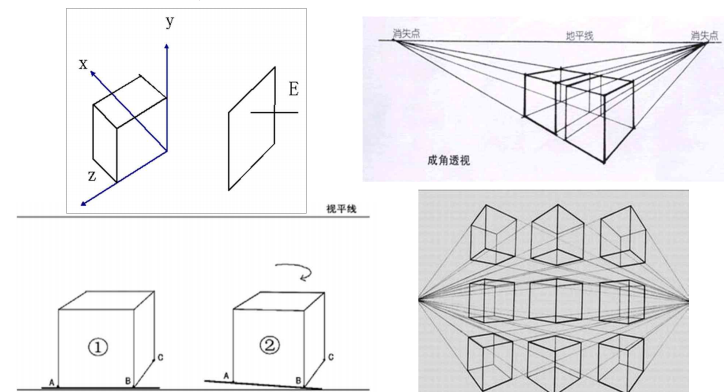
两点透视(成角透视)

某一条主轴与画面平行，另外两主轴与画面相交
透视图有两个主灭点

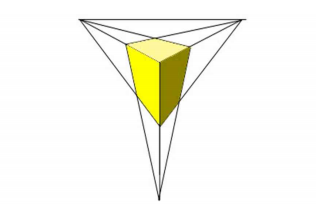
三点透视(斜透视)
三条主轴均与画面相交
产生三个主灭点

opengl编程实践

glMatrixMode(GL_MODELVIEW);
gluLookAt();
glMatrixMode(GL_PROJECTION);
glFrustum();
gluPerspective();

gluPerspective();

这个函数原型为:
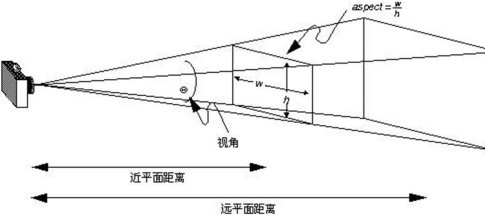
void gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear,GLdouble zFar);

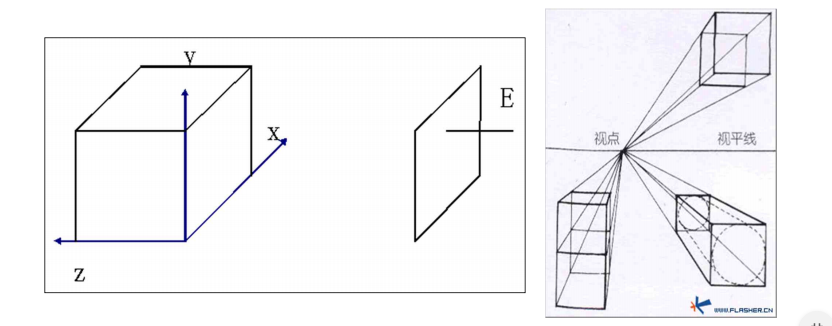
创建一个对称的透视型视景体，但它的参数定义于前面的不同，如图。其操作是创建-一个对称的透视投影矩阵，并且用这个矩阵乘以当前矩阵。参数fovy定义视野在Y-Z平面的角度，范围是[0.0, 180.0]; 参数aspect是投影平面宽度与高度的比率;参数Near和Far分别是近远裁剪面到视点(沿Z负轴)的距离，它们总为正值。

glFrustum();

这个函数原型为:
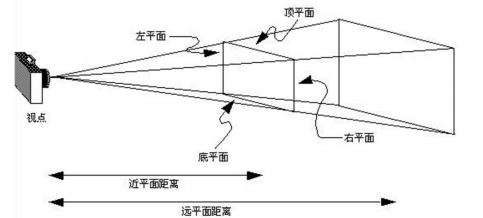
void glFrustum(GLdouble left, GLdouble Right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far);
创建一个透视型的视景体。其操作是创建一个透视投影的矩阵，并且用这个矩阵乘以当前矩阵。这个函数的参数只定义近裁剪平面的左下角点和右上角点的三维空间坐标，即(left,bottom,-near)和(right， top， -near) ;最后一个参数far是远裁剪平面的离视点的距离值，其左下角点和右上角点空间坐标由函数根据透视投影原理自动生成。near和far表示离视点的远近，它们总为正值(near/far必须>0)。