图形几何变换
图形变换是计算机图形学中的一个重要内容。通过对简单图形进行多种变换和组合,可以形成一个复杂图形,这些操作也用于将世界坐标系中的场景描述转换为输出设备上的观察显示中。
应用于对象几何描述并改变它的位置、方向或大小等几何信息的操作称为几何变换(Geometric Transformation)。这种变换一般维持图形的拓扑关系(构成规则)不变,只改变图形的几何关系(大小、形状及相对位置),主要包括平移、放缩、旋转及投影等操作。
平移变换
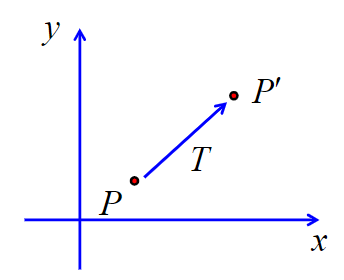
\[P=\begin{bmatrix}
x
\\
y
\end{bmatrix}
{P}'=\begin{bmatrix}
{x}'
\\
{y}'
\end{bmatrix}
T=\begin{bmatrix}
t_{x}
\\
t_{y}
\end{bmatrix}\]
\[{P}'=P+T
\]
通过齐次坐标变换矩阵表示
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix}1 & 0 & t_{x}\\ 0 & 1 & t_{y} \\ 0 & 0& 1 \end{bmatrix}\cdot\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}=
T(t_{x},t_{y})\cdot P
\]
绕坐标原点的旋转变换
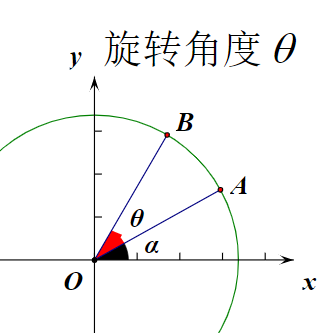
旋转角定向:逆时针为正,顺时针为负
\[cos(\alpha + \theta )= cos(\alpha)cos(\theta) - sin(\alpha)sin(\theta)
\]
\[sin(\alpha + \theta )= sin(\alpha)cos(\theta) + cos(\alpha)sin(\theta)
\]
\[OA=\begin{bmatrix}
rcos(\alpha)
\\
rsin(\alpha)
\end{bmatrix}
OB=\begin{bmatrix}
rcos(\alpha + \theta )
\\
rsin(\alpha + \theta )
\end{bmatrix}
T=\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta
\end{bmatrix}\]
\[OB=OA \cdot T
\]
通过齐次坐标变换矩阵表示
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix}cos \theta & -sin \theta & 0\\ sin \theta & cos \theta & 0 \\ 0 & 0& 1 \end{bmatrix}\cdot\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}=
R(\theta) \cdot P
\]
以坐标原点为基准点的缩放变换
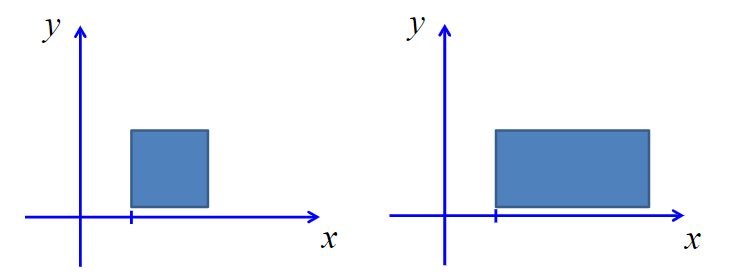
\[{x}'=x \cdot s_{x}
\]
\[{y}'=y \cdot s_{y}
\]
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \end{bmatrix}
=\begin{bmatrix}s_{x} & 0\\ 0 & s_{y} \end{bmatrix}\cdot\begin{bmatrix}x\\ y \end{bmatrix}=
s \cdot P\]
通过齐次坐标变换矩阵表示
\[{x}'=x \cdot s_{x}
\]
\[{y}'=y \cdot s_{y}
\]
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix} s_{x} & 0 & 0\\ 0 & s_{y} & 0 \\ 0 & 0& 1 \end{bmatrix}\cdot\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}=
S(S_{x},s_{y}) \cdot P
\]
反射变换
产生对象镜像的变换称为反射(reflection),变换通过将对象绕反射轴旋转180°来生成反射镜像
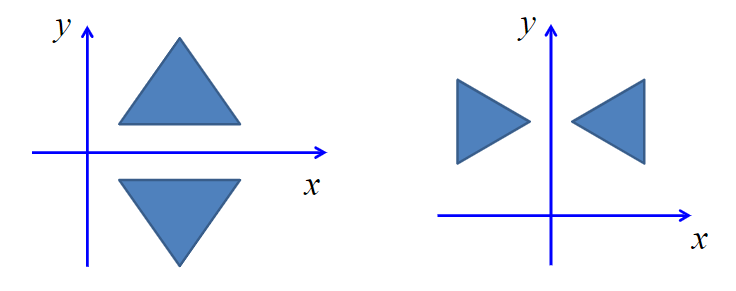
1 相对于x轴的反射
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}
=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
2 相对于y轴的反射
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}=
\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
3 相对于坐标原点的反射
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}=
\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
通过齐次坐标变换矩阵表示
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix} a & b & 0\\ c & d & 0 \\ 0 & 0& 1
\end{bmatrix} \cdot
\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}
=R(a,b,c,d) \cdot P
\]
4 相对于任意点的反射
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix} -1 & 0 & 2u\\ 0 & -1 & 2v \\ 0 & 0& 1
\end{bmatrix} \cdot
\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}
=T \cdot P
\]
5 关于对角线 y= x 的反射
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}=
\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
6 关于对角线 y= -x 的反射
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}=
\begin{bmatrix} 0 & -1 \\ -1 & 0 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
7 相对于任意直线 y=mx+b 的反射
\[p'=
\begin{bmatrix}
x'\\
y' \\
1
\end{bmatrix}
=
\frac{1}{1+m^{2}}
\begin{bmatrix}
1-m^{2} & 2m & -2mb\\
2m & m^{2}-1 & 2b\\
0 & 0 & 1+m^{2}
\end{bmatrix}
\cdot
\begin{bmatrix}
x\\
y \\
1
\end{bmatrix}
=T\cdot P
\]
推导
错切变换
错切(shear)是一种使对象形状发生变化的变换,经过错切的对象好像是由相互滑动的内部夹层组成
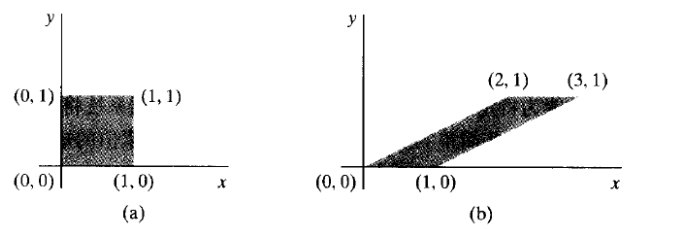
相对于x轴的x方向错切由下列变换产生
\[ \begin{bmatrix} {x}' \\ {y}' \end{bmatrix}
=\begin{bmatrix} 1 & sh_{x} \\ 0 & 1 \end{bmatrix} \cdot
\begin{bmatrix} x \\ y \end{bmatrix} \]
该变换对应的坐标转换为
\[{x}'=x+sh_{x} \cdot y
\]
\[{y}'=y
\]
通过齐次坐标变换矩阵表示
相对于线\(y=y_{ref}\)的x方向错切
\[ \begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix} 1 & sh_{x} & -sh_{x} \cdot y_{ref} \\ 0 & 1 & 0 \\ 0 & 0& 1
\end{bmatrix} \cdot
\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}
\]
相对于线\(x=x_{ref}\)的y方向错切
\[ \begin{bmatrix}{x}'\\ {y}' \\ 1 \end{bmatrix}
=\begin{bmatrix} 1 & 0 & 0 \\ sh_{y} & 1 & -sh_{y} \cdot x_{ref}\\ 0 & 0& 1
\end{bmatrix} \cdot
\begin{bmatrix}x\\ y \\ 1 \end{bmatrix}
\]
逆变换
通过齐次坐标变换矩阵表示
平移逆变换
\[T^{-1} =\begin{bmatrix} 1 & 0 & -t_{x} \\ 0 & 1 & -t_{y} \\ 0 & 0& 1
\end{bmatrix}
\]
旋转逆变换
\[R^{-1} =\begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0& 1 \end{bmatrix}
\]
缩放逆变换
\[S^{-1} =\begin{bmatrix} \frac{1}{s_{x}} & 0 & 0 \\ 0 & \frac{1}{s_{y}} & 0 \\ 0 & 0& 1
\end{bmatrix}
\]
二维复合变换
利用矩阵表达式,可以通过计算单个变换的矩阵乘积,将任意的变换序列组成复合变换矩阵。形成变换矩阵的乘积经常称为矩阵的合并或复合。由于坐标点位置已经用齐次列矩阵表示,故必须将变换矩阵序列依次先乘该列矩阵。由于场景中许多位置用相同的顺序变换,因此先将所有变换矩阵相乘形成一个复合矩阵将是高效率的方法。
因此,如果对点位置P进行两次变换,变换后的位置将用下式计算
\[{P}'=M_{1} \cdot M_{2} \cdot P = M \cdot P
\]
\(该坐标位置可采用矩阵M来变换,而不是单独地先用M_{1}然后再用M_{2}来变换\)
二维基本复合变换
1 复合二维平移
\[\begin{bmatrix} 1 & 0 & t_{2x} \\ 0 & 1 & t_{2y} \\ 0 & 0& 1 \end{bmatrix}
\cdot
\begin{bmatrix} 1 & 0 & t_{1x} \\ 0 & 1 & t_{1y} \\ 0 & 0& 1 \end{bmatrix}
=
\begin{bmatrix} 1 & 0 & t_{1x}+t_{2x} \\ 0 & 1 & t_{1y}+t_{2y} \\ 0 & 0& 1 \end{bmatrix}
\]
\[T(t_{2x},t_{2y}) \cdot T(t_{1x},t_{1y}) = T (t_{1x}+t_{2x},t_{1y}+t_{2y} )
\]
2 复合二维旋转
\[\begin{bmatrix}
cos \theta_{1} & -sin \theta_{1} & 0
\\ sin \theta_{1} & cos \theta_{1} & 0
\\ 0 & 0& 1
\end{bmatrix}
\cdot
\begin{bmatrix}
cos \theta_{2} & -sin \theta_{2} & 0
\\ sin \theta_{2} & cos \theta_{2} & 0
\\ 0 & 0& 1
\end{bmatrix}
=
\begin{bmatrix}
cos (\theta_{1}+\theta_{2}) & -sin (\theta_{1}+\theta_{2}) & 0
\\ sin (\theta_{1}+\theta_{2}) & cos (\theta_{1}+\theta_{2}) & 0
\\ 0 & 0& 1
\end{bmatrix}
\]
\[R( \theta_{1}) \cdot R(\theta_{2}) = R(\theta_{1} + \theta_{2})
\]
3 复合二维缩放
\[\begin{bmatrix} s_{2x} & 0 & 0 \\ 0 & s_{2y} & 1 \\ 0 & 0& 1 \end{bmatrix}
\cdot
\begin{bmatrix} s_{1x} & 0 & 0 \\ 0 & s_{1y} & 1 \\ 0 & 0& 1 \end{bmatrix}
=
\begin{bmatrix} s_{2x} \cdot s_{1x} & 0 & 0 \\ 0 & s_{2y} \cdot s_{1y} & 1 \\ 0 & 0& 1 \end{bmatrix}
\]
\[S(s_{2x},s_{2y}) \cdot S(s_{1x},s_{1y}) = S (s_{1x} \cdot s_{2x},s_{1y} \cdot s_{2y} )
\]
二维通用复合变换
基准点旋转
平移对象使基准点位置移动到坐标原点
绕坐标原点旋转
平移对象使基准点回到其原始位置
\[T(x_{r},y_{r}) \cdot R(\theta) \cdot T(-x_{r},-y_{r}) = R(x_{r},y_{r},\theta)
\]
基准点缩放
平移对象使固定点与坐标原点重合
对坐标原点为基准点进行缩放
反向平移将对象返回到原始位置
\[T(x_{r},y_{r}) \cdot S(s_{x},s_{y}) \cdot T(-x_{r},-y_{r}) = R(x_{r},y_{r},s_{x},s_{y})
\]
定向缩放
将对象所希望的缩放方向旋转到与坐标轴一致,进行缩放后再逆向旋转至原来方位。
\[R^{-1}(\theta) \cdot S(s_{x},s_{y}) \cdot R(\theta)
\]
二维坐标系间的变换
计算机图形应用经常需要在场景处理的各阶段将对象的描述从一个坐标系变换到另一个坐标系。观察子程序将对象描述从世界坐标系变换到设备坐标系。对于建模和设计应用,每个对象在各自的局部笛卡尔坐标系中设计。这些局部坐标描述必须接着变换到整个场景坐标系的相应位置和方向。
同样,有时场景在利用对象对称性的非笛卡尔参考系描述。在这些系统中的对象描述必须转换到笛卡尔世界坐标系中进行处理。
三维几何基本变换
三维基本几何变换都是相对于坐标原点和坐标轴进行的几何变换
假设三维形体变换前一点为p(x,y,z),变换后为p'(x',y',z')。
平移变换
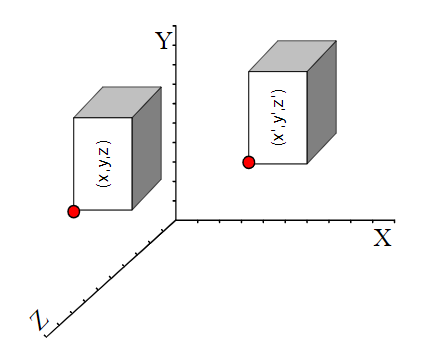
通过齐次坐标变换矩阵表示
\[{P}'=\begin{bmatrix}{x}'\\ {y}' \\ {z}' \\ 1 \end{bmatrix}
=\begin{bmatrix}1 & 0 & 0 & t_{x}\\ 0 & 1 & 0&t_{y} \\ 0 & 0& 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix}x\\ y \\ z \\ 1 \end{bmatrix}
\]
绕坐标原点的旋转变换
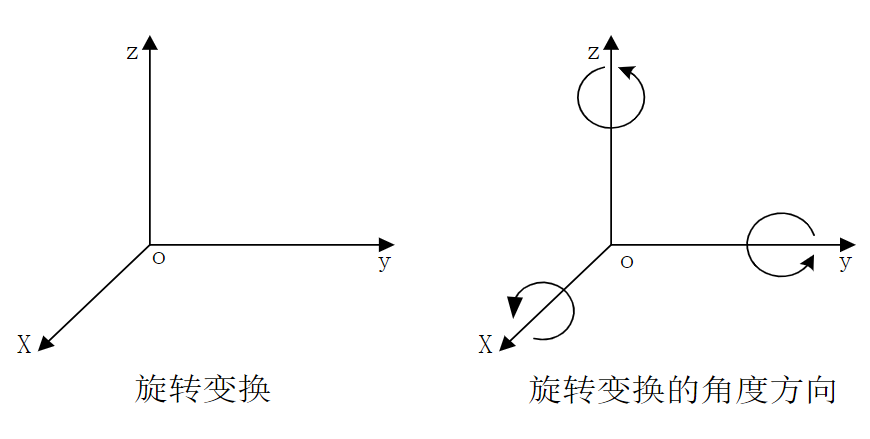
通过齐次坐标变换矩阵表示
- 绕x轴旋转
\[T_{RX}
=\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & cos \theta & -sin \theta & 0\\
0 & sin \theta & cos \theta & 0 \\
0 & 0 & 0& 1
\end{bmatrix}
\]
- 绕y轴旋转
\[T_{RY}
=\begin{bmatrix}
cos \theta & 0 & sin \theta & 0 \\
0 & 1 & 0 & 0\\
-sin \theta & 0 & cos \theta & 0 \\
0 & 0 & 0& 1
\end{bmatrix}
\]
- 绕z轴旋转
\[T_{RZ}
=\begin{bmatrix}
cos \theta & -sin \theta & 0 & 0 \\
sin \theta & cos \theta & 0 & 0\\
0 & 0 & 1 & 0 \\
0 & 0 & 0& 1
\end{bmatrix}
\]
缩放变换
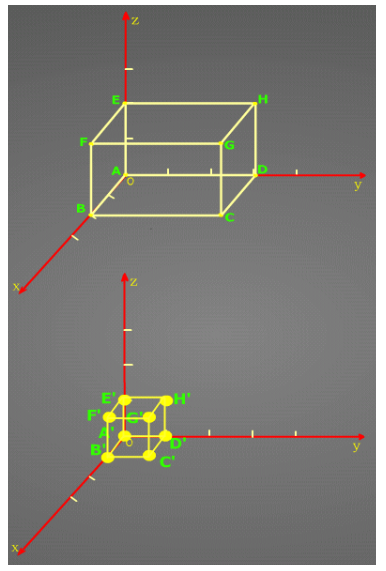
通过齐次坐标变换矩阵表示
\[T_{S}
=\begin{bmatrix}
S_{x} & 0 & 0 & 0 \\
0 & S_{y} & 0 & 0\\
0 & 0 & S_{z} & 0 \\
0 & 0 & 0& 1
\end{bmatrix}
\]
三维复合变换
三维复合变换是指图形作一次以上的基本变换,变换结果是基本变换矩阵相乘
图形几何变换的模式
变换合成的方法大大提高了对图形对象依次做多次变换时的效率,同时变换合成也提供了一种构造复杂变换的方法。需要对图形对象进行的复杂变换也可以分解成为多个简单的基本变换,再依次将其作用于图形
固定坐标系模式(相对于原始坐标系)
相对于同一个固定坐标系,每一次变换均可看成相对于原始坐标系执行
先调用的变换先执行,后调用的变换后执行
矩阵合并时,先调用的矩阵放在右边,后调用的矩阵放在左边,也称为固定坐标系模式
活动坐标系模式(堆栈结构调用)
又称空间模式,连续执行几个变换时,变换矩阵的合并方式与固定坐标系模式相反。
先调用的变换乘在连乘式左边,而后调用的变换乘在连乘式右边。
体现在程序执行方式上,即为先调用的变换后执行,后调用的变换先执行。
该模式非常适合堆栈结构实现,也是OpenGL图形库所采用的方式










