opengl算法学习---直线裁剪算法
裁剪是从数据集合提取信息的过程,它是计算机图形学许多重要问题的基础。裁剪典型的用途就是从一个大的场景中提取所需的信息,以显示某一局部场景或视图。比如浏览地图时,对感兴趣的区域放大显示,此时窗口内显示的内容会相应减少。确定图形的哪些部分在窗口内,哪些部分在窗口外(不可见区域),只显示窗口内的那部分图形,这个选择处理过程就是裁剪。
这里详细讲述两种算法
Cohen-Sutherland编码裁剪算法
Cohen-Sutherland编码裁剪算法
算法思想
1)若线段完全在窗口之内则显示该线段称为“取”,
2)若线段明显在窗口之外则丢弃该线段称为“弃”
3)若线段既不满足“取”的条件也不满足“弃”的条件则把线段分割为两段,对于完全在窗口之外的部分可弃之。
具体实现
为快速判断一条直线段与矩形窗口的位置关系采用如图所示的空间划分和编码方案(四位二进制编码上下右左)

裁剪一条线段时先求出两端点所在的区号,若皆为零保留。
若端点编码按位取与运算的结果不为零,意味着线段位于窗口之外,应舍弃。
否则求出线段与窗口某边的交点并将该线段一分为二后,舍弃完全在窗口外的线段并对另一段重复上述处理。
代码实现
稍后再补
Liang-Barsky算法
概念
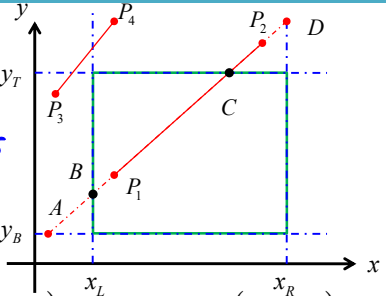
Liang-Barsky算法的基本思想是,从 A、B 和 P1中找出最靠近 P2的点,如图所示为 P1;从C 、D 和 P2中找出最靠近P1的点,显然为C 点;也即 PC1即为裁剪后部分。
具体实现
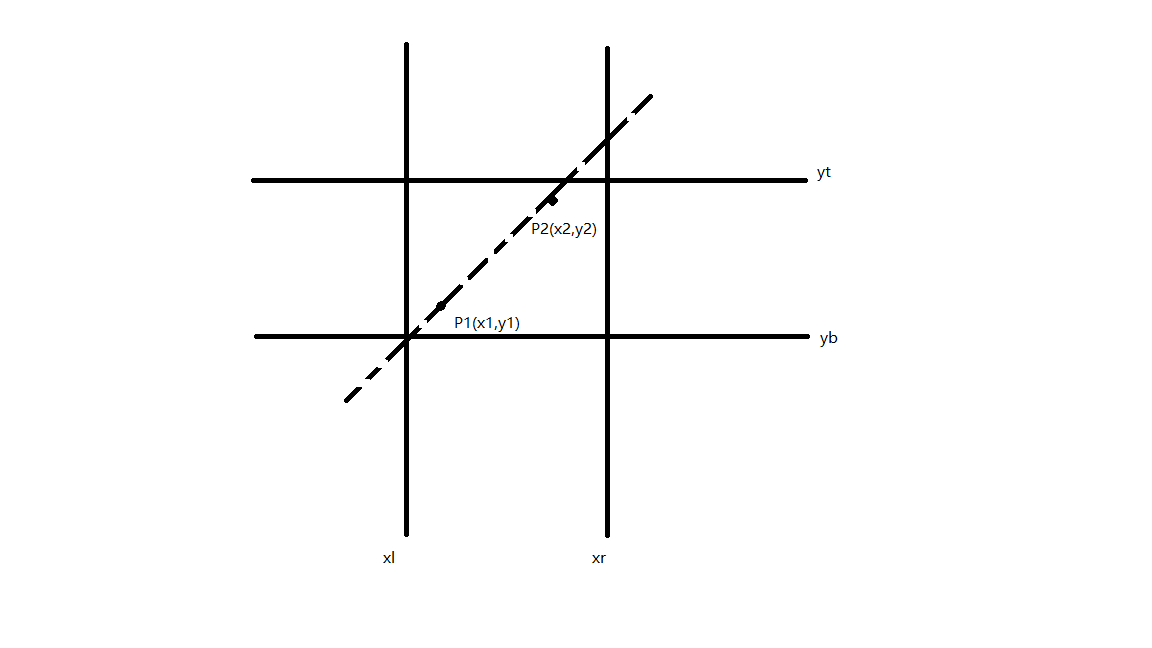
对于区域内存在的线段P1P2,根据两点坐标构造方程
令\(\Delta x=x_{2}-x_{1} \Delta y=y_{2}-y_{1}\)
即可推出
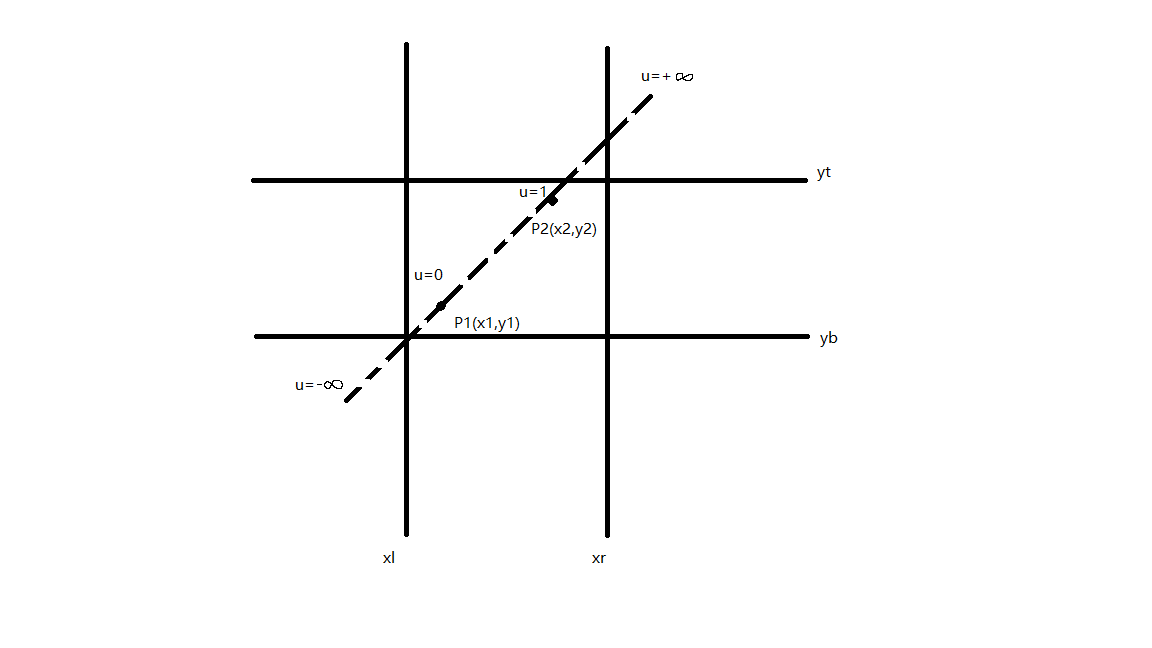
Liang-Barsky算法通过计算两端点截取后的u值,绘制截取后的线段,设截取后线段的两端点u为\(u_{1}、u_{2}\)
\(u_{1}\)初始值=0,即线段初始点,\(u_{2}\)初始值=1,即线段终点
对于x而言
同理
即可推得
构造
每个k对应上式每种情况
当\(p_{k}=0\)时,该线段平行于轮廓线
如果\(q_{k}<0\)
当k=1时,\(x_{r}<x_{1}\)
当k=2时,\(x_{1}<x_{l}\)
当k=3时,\(y_{t}<y_{1}\)
当k=4时,\(y_{1}<y_{b}\)
可推出若\(q_{k}<0\)时,该线段位于裁剪区域外
如果\(q_{k}\geqslant 0\)
则该线段位于区域内
当\(p_{k} \neq 0\)时,
此时线段延长线与轮廓线交点在上式中u值\(=\frac{q_{k}}{p_{k}}\)
若\(p_{k}<0\) 则该线段部分为由边界外到边界内,\(u_{1}=max(u_{1},u)\)
若\(p_{k}>0\) 则该线段部分为由边界内到边界外,\(u_{2}=min(u_{2},u)\)
通过以上过程,可推出截取后线段两端点的\(u_{1}\)与\(u_{2}\),若\(u_{1}>u_{2}\),则该线段不为于裁剪区域内
代码实现
void LiangBarsky(Point p1,Point p2,Rectan rec)
{
float u1=0,u2=1,p[4],q[4];
p[0]=p1.x-p2.x;p[1]=p2.x-p1.x;
p[2]=p1.y-p2.y;p[3]=p2.y-p1.y;
q[0]=p1.x-rec.xl;q[1]=rec.xr-p1.x;
q[2]=p1.y-rec.yb;q[3]=rec.yt-p1.x;
for(int i=0;i<4;i++)
{
if(!p[i] && q[i]<0) return ;
else if(p[i])
{
float u=q[i]/p[i];
if(p[i]<0) u1=max(u1,u);
else u2=min(u2,u);
}
}
if(u1>u2) return ;
drawline(Point(p1.x+u1*(p2.x-p1.x),p1.y+u1*(p2.y-p1.y)),Point(p1.x+u2*(p2.x-p1.x),p1.y+u2*(p2.y-p1.y)),BLUE);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号