opengl算法学习---直线绘制
opengl算法学习--直线绘制
DDA方法
DDA方法(Digital Differential Analyzer)是一种线段扫描转换算法,在一个坐标轴上以单位间隔对线段取样,从而确定另一个坐标轴上最靠近线路径的对应整数值。
方法概述
假设已知直线两端点\(A(x_{a},y_{a})\),\(B(x_{b},y_{b})\)
\(\Delta x=x_{b}-x_{a}\) \(\Delta y=y_{b}-y_{a}\)
已知直线的斜截式方程为y=m* x+b (\(m=\frac{\Delta y}{\Delta x}\))
当\(m\in(0,1)\)时,以单位x间隔(\(\delta x=1\)),逐次计算y值
当\(m\in(1,\infty)\)时,以单位y间隔(\(\delta y=1\)),逐次计算x值
对计算出的x与y,要经过四舍五入后置入像素位置
如斜率m<0时,可以通过取m绝对值,从终点向起点绘制
代码实现
#include <GL/gl.h>
#include <GL/glut.h>
using namespace std;
void init()
{
glClearColor (0.0, 0.0, 0.0, 0.0);
glMatrixMode (GL_PROJECTION);
gluOrtho2D (0, 500, 0, 500);
}
inline int Round(int x) {return int(x+0.5);}
void Setpoint(float x,float y)
{
glPointSize(2);
glBegin(GL_POINTS);
glVertex2i(Round(x+0.5),Round(y+0.5));
glEnd();
glFlush();
}
void DDALine(int sx,int sy,int ex,int ey)
{
int dx=ex-sx,dy=ey-sy;
float x=sx,y=sy;
double step;
if(abs(dx)>abs(dy)) step=abs(dx);
else step=abs(dy);
double addx=dx/step;
double addy=dy/step;
Setpoint(x,y);
for(int k=0; k<=step; ++k)
{
x+=addx;y+=addy;
Setpoint(x,y);
}
}
void display()
{
glClear(GL_COLOR_BUFFER_BIT);
DDALine(100,100,400,400);
}
int main(int argc, char *argv[])
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);
glutInitWindowPosition(100, 100);
glutInitWindowSize(500, 500);
glutCreateWindow("a dda line");
init();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
DDA算法利用光栅特性消除了直线方程中的乘法,通过在x或y方向使用合适的增量,从而沿线路径逐步得到各像素的位置。但由于浮点增量的存在,使得该方法对于长线段存在较大误差,且浮点运算耗时也相对较大
Bresenham画线算法
Bresenham画线算法是应用最广泛的直线生成算法,它采用加减与乘2运算(即移位运算)来实现。
举例说明,对于一条斜率为\(m\in (0,1)\)的直线,可以预测到在原点的基础上的下一个绘制点,必定为T或者S,因此,可以通过比较TS两点对直线的纵向距离t与s,来确定下一个绘制点
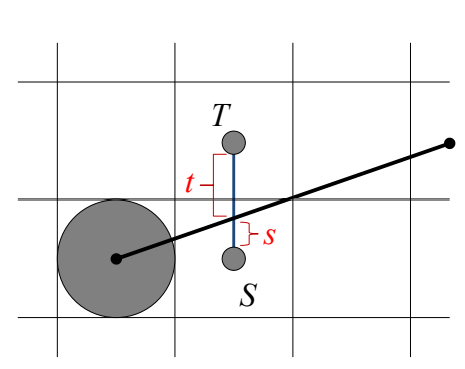
方法概述
当\(m\in(0,1)\)时,选取x轴为计步方向
设原点为( \(x_{i}\) , \(y_{i}\) ),则S( \(x_{i+1}\) , \(y_{i}\) ),T( \(x_{i+1}\) , \(y_{i+1}\) )
令
可得
当\(d_{i}\)>0时 \(y_{i+1}=y_{i}+1\)
当\(d_{i}\)<0时 \(y_{i+1}=y_{i}\)
当i=1时,\(y_{i}=mx_{i}+b\)
所以
当\(m\in(1,\infty)\)时,选取y轴为计步方向
设原点为( \(x_{i}\) , \(y_{i}\) ),则S( \(x_{i+1}\) , \(y_{i}\) ),T( \(x_{i+1}\) , \(y_{i+1}\) )
令\(k=\frac{1}{m}\)
令
可得
当\(d_{i}\)>0时 \(x_{i+1}=x_{i}+1\)
当\(d_{i}\)<0时 \(x_{i+1}=x_{i}\)
当i=1时,\(x_{i}=k(y_{i}-b)\)
所以
当m<0时,可视为反向绘制,因此适用上式
代码实现
void Bresenham(int sx,int sy,int ex,int ey)
{
int dx=abs(sx-ex),dy=abs(sy-ey);
bool flag=false;
if(dy>dx)
{
swap(dx,dy);
swap(sx,sy);
swap(ex,ey);
flag=true;
}
int d=(dy<<1)-dx;
int d1p=(dy-dx)<<1,d1d=dy<<1;
int x=sx,y=sy;
int ix = (ex - sx) > 0 ? 1 : -1,iy = (ey - sy) > 0 ? 1 : -1;
if(!flag) Setpoint(x,y);
else Setpoint(y,x);
while (x!=ex)
{
x+=ix;
if(d<0) d+=d1d;
else
{
y+=iy;
d+=d1p;
}
if(!flag) Setpoint(x,y);
else Setpoint(y,x);
}
}
Bresenham画线算法相比DDA算法,因为没有浮点运算,因此更加效率