图：1928.规定时间内到达终点的最小花费，题解：动态规划方法

1928. 规定时间内到达终点的最小花费 - 力扣（LeetCode）

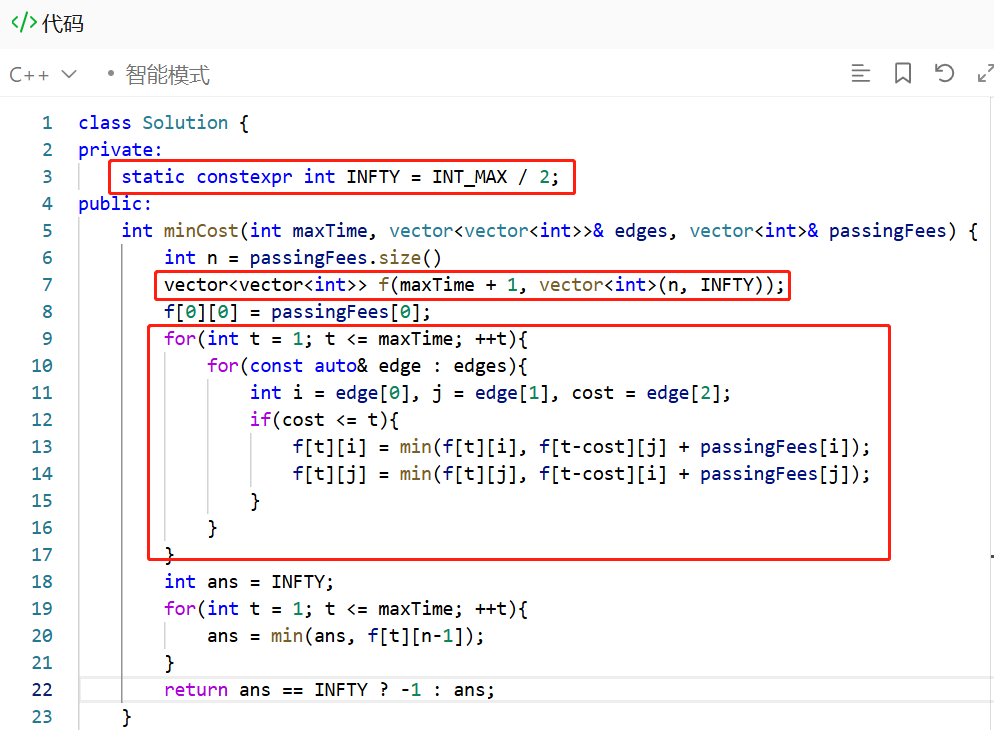
有点难，参考官方题解代码：

利用了动态规划思想，逐步计算从起点到各个城市在不同时间下的最小费用。

 1.代码解释，涉及，static关键字，constexpr关键字，INT_MAX除以2赋值的含义

static constexpr int INFTY = INT_MAX / 2;

 1. **`static` 关键字**：
- **`static`** 表示这个变量具有**静态存储周期**，意味着它只在内存中存储一份，并且生命周期从程序开始到程序结束。它也意味着该变量的作用域限制在声明它的类或文件中，不会被外部直接访问。通常用在类或函数内部，或者在全局作用域中限制变量的可见性。

 2. **`constexpr` 关键字**：
- **`constexpr`** 表示这是一个**常量表达式**，在编译时就能确定它的值。与 `const` 类似，但它更严格，要求编译器在编译时对表达式求值。换句话说，`constexpr` 变量必须能够在编译阶段被计算出其值。

 3. **`int INFTY`**：
- **`INFTY`** 是定义的一个整数常量，表示无穷大。这个常量是整型（`int`），并且通过 `static constexpr` 限定，它的值在编译时确定，并且在类或文件的整个生命周期内都有效。

 4. **`INT_MAX / 2`**：
- **`INT_MAX`** 是在 `climits` 头文件中定义的一个宏，表示 **int 类型能够表示的最大值**，通常是 `2,147,483,647`（对于 32 位的 `int` 类型）。
- 使用 `INT_MAX / 2` 而不是 `INT_MAX` 的原因是为了防止在执行某些算法时，防止数值溢出。很多时候我们在图算法或者动态规划中使用 "无穷大" 来表示不可达的节点或状态。如果直接使用 `INT_MAX`，在计算时（比如加权图中更新路径长度时）可能会导致数值溢出（因为超过了 `INT_MAX` 的范围）。而使用 `INT_MAX / 2` 可以让值足够大，但避免溢出的风险。

总结：
这行代码定义了一个 **`INFTY`** 常量，表示一个**非常大的值**（接近于 `INT_MAX`，但小一半），用于表示类似“无穷大”的含义，常见于**图算法**（如 Dijkstra 最短路径）或者动态规划中，作为初始化的最大值。它使用了 `static constexpr`，所以它的值是在编译时就确定的，且在整个程序生命周期中只会存在一份。

2.

vector<vector<int>> f(maxTime + 1, vector<int>(n, INFTY));

这一行代码的作用是定义一个二维动态数组 `f`，其中 `f[t][i]` 表示在使用了 `t` 时间时，能够到达城市 `i` 的最小费用。详细解释如下：

 1. **定义二维数组 `f`**：

- `f` 是一个大小为 `(maxTime + 1) x n` 的二维数组。
- 第一维：时间，从 `0` 到 `maxTime`，共 `maxTime + 1` 行，表示可以使用的时间。
- 第二维：城市，从 `0` 到 `n-1`，表示共有 `n` 个城市。

 2. **`vector<int>(n, INFTY)`**：
- 这一部分表示创建一个长度为 `n` 的一维数组，每个元素都初始化为 `INFTY`。
- `n` 是城市的数量。
- `INFTY` 是一个表示“无穷大”的值，表示无法在当前状态下到达某个城市。
- 也就是一开始所有城市的通行费用都设置为一个极大值（表示不可能到达）。

 3. **构建二维数组**：
- `vector<vector<int>> f(maxTime + 1, ...)`：创建 `maxTime + 1` 行，每一行是一个长度为 `n` 的数组，每个元素初始为 `INFTY`。
- 因此，`f` 是一个二维数组，表示在不同时间下到达不同城市的最小通行费用。每个城市在每个时间点的初始状态都是不可达（`INFTY`）。