交叉熵代价函数（04-1）

二次代价函数

C=12n∑x1,...xn∥y(x)−aL(x)∥2C=12n∑x1,...xn‖y(x)−aL(x)‖2

其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数；整个的意思就是把n个y-a的平方累加起来，再除以2求一下均值。

为简单起见，先看下 一个样本 的情况，此时二次代价函数为：C=(y−a)22C=(y−a)22

a=σ(z),z=∑wj∗xj+ba=σ(z),z=∑wj∗xj+b  ，其中a就代表激活函数的输出值，这个符号σσ代表sigmoid函数将变量映射到0-1的SS型光滑的曲线，z是上一层神经元信号的总和

假如我们使用梯度下降发(Gradient descent)来调整权值参数的大小，权值w和权值b的梯度推到如下(求导数)：

   ∂C∂w=(a−y)σ′(z)x∂C∂w=(a−y)σ′(z)x    ∂C∂b=(a−y)σ′(z)∂C∂b=(a−y)σ′(z)

其中，z表示神经元的输入，σσ表示激活函数sigmoid。可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整越快，训练收敛的就越快。

 

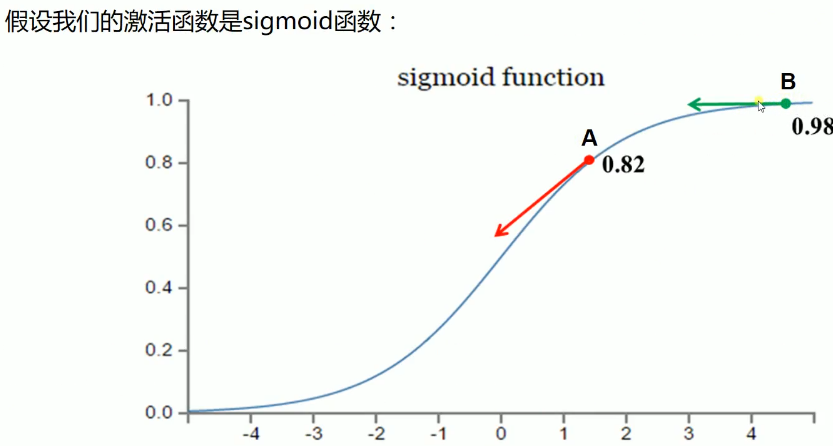
 假设我们激活函数输出的值目标是收敛到1，A点离目标较远，梯度较大，权值调整比较大。B点为0.98离目标比较近，梯度比较小，权值调整比较小，调整方案合理。

 假设我们激活函数输出的值目标是收敛到0，A点离目标较远，梯度较大，权值调整比较大。B点为0.98离目标比较远，梯度比较小，权值调整比较小，调整方案不合理，B点要经过非常长的时间才会收敛到0，而且B点很可能成为不收敛的点。

 

交叉墒代价函数(cross-entropy)

由于上边的问题，我们换一种思路，我们不改变激活函数，而是改变代价函数，改用交叉墒代价函数：

C=−1n∑x1,,,xn,[ylna+(1−y)ln(1−a)]C=−1n∑x1,,,xn,[yln⁡a+(1−y)ln⁡(1−a)]

其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。

a=σ(z),z=∑wj∗xj+ba=σ(z),z=∑wj∗xj+b σ′(z)=σ(z)(1−σ(x))σ′(z)=σ(z)(1−σ(x)) sigmod函数的导数比较好求，这也是为什么大家用sigmoid做激活函数的原因，接下来我们看一下求导的过程

 

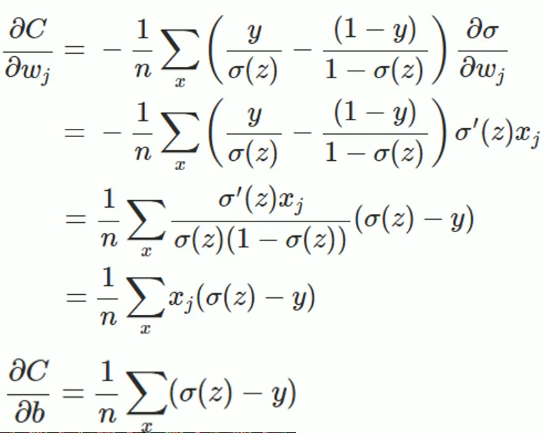
懒得敲了，直接贴个图过来，之后闲了在敲一遍，上边就是求导的推导过程，从最后的式子可以看出：权值w和偏执值b的调整与σ′(z)σ′(z)无关，另外，梯度公式中的σ(z)−yσ(z)−y表示输出值与实际值放入误差。所以当误差越大时，梯度就越大，参数w和b的调整就越快，训练的速度也就越快。

总结：当输出神经元是线性的，那么二次代价函数就是一种合适的选择。如果输出神经元是S型函数，那么比较适合交叉墒代价函数。

对数似然代价函数（log-likelihood cost）

对数似然函数常用来作为softmax回归的代价函数，如果输出层神经元是sigmoid函数，可以使用交叉墒代价函数。而深度学习中更普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数似然代价函数。

对数似然代价函数与softmax的组合和交叉墒与sigmoid函数的组合非常相似。对数似然代价函数在二分类时可以化简为交叉墒代价函数的形式。

在TensorFlow中用：

tf.nn.sigmoid_cross_entropy_with_logits()来表示跟sigmoid搭配使用的交叉墒。

tf.nn.softmax_cross_entropy_with_logits()来表示跟softmax搭配使用的交叉墒。

代码中黄色是对上节代码的优化

使用交叉熵代价函数，加快模型迭代的速度，有助于模型快速收敛，可以节省训练模型的时间。在适时地时候使用交叉熵作为代价函数，效果会好很多

loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=prediction))

# -*- coding: UTF-8 -*-

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
 
#载入数据集
mnist=input_data.read_data_sets("MNIST_data", one_hot=True)
 
#每个批次的大小
batch_size=100
#计算一共有多少个批次
n_batch=mnist.train.num_examples // batch_size
 
#定义两个placeholder
x=tf.placeholder(tf.float32,[None,784])
y=tf.placeholder(tf.float32,[None,10])
 
#创建一个简单的神经网络
W=tf.Variable(tf.zeros([784,10]))
b=tf.Variable(tf.zeros([1,10]))
prediction=tf.nn.softmax(tf.matmul(x,W)+b)
 

#二次代价函数
#loss = tf.reduce_mean(tf.square(y-prediction))
#使用交叉熵代价函数，加快模型迭代的速度，有助于模型快速收敛，可以节省训练模型的时间。在适时地时候使用交叉熵作为代价函数，效果会好很多
loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=prediction))
#使用梯度下降法优化
train_step=tf.train.GradientDescentOptimizer(0.2).minimize(loss)
 
#初始化变量
init=tf.global_variables_initializer()
 
#结果放在一个布尔型列表中
correct_prediction=tf.equal(tf.argmax(y,1), tf.argmax(prediction,1)) #argmax函数返回一维向量中最大值所在的位置
#求准确率
accuracy=tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
 
with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):#把所有图片训练21遍
        for batch in range(n_batch):#把所有图片都训练一遍
            batch_xs,batch_ys=mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs, y:batch_ys})
 
        acc=sess.run(accuracy,feed_dict={x:mnist.test.images, y:mnist.test.labels})
        print("Iter"+str(epoch)+",Testing Accuracy "+str(acc))

运行结果：

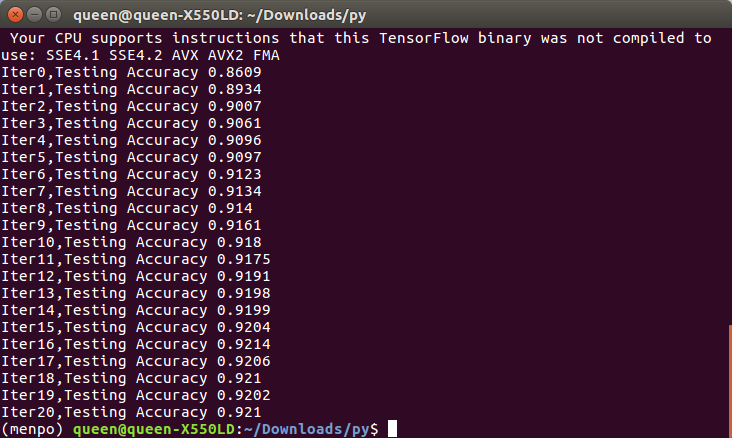
发现使用了交叉熵代价函数时发现迭代第2次就达到90%，而用的二次代价函数迭代第7次才达到90%（上节用的是二次代价函数）。准确率也提高了1%