编译原理语法分析之LL(1) parser
一、 数据组成部分:
- input buffer——待分析的字符串,以$结尾
- output——最左推导的产生式
- stack——栈底部为$,包含grammar symbols
- parsing table——二维数组M[A,a],row表示非终结符,col表示终结符或者$,每一个entry标注一条产生式或者error

二、 LL(1) Parser——步骤
- 产生式分解:将 B->bB|ε 分解成两条 B->bB和B->ε
- 求FIRST集和FOLLOW集
- 根据FIRST和FOLLOW集构建parsing table
- 初始化栈:$ 初始化input:字符串$
- 分析栈得出输出产生式
α是grammar symbols中一个字符串,FIRST(α)是出现在α的leftmost的所有可能终结符
-
If X is a terminal, FIRST(X) = {X}
- If X → ε is a production rule, add ε to FIRST (X)
-
If X is a non-terminal, and X→ Y1Y2…Yk is a production rule
Place FIRST(Y1) in FIRST (X) if Y1→ ε,
Place FIRST (Y2) in FIRST(X) if Y2 → ε,
Place FIRST(Y3) in FIRST(X) … if Yk-1 → ε,
Place FIRST(Yk) in FIRST(X)
NOTE: As soon as Yi → ε , Stop.
NOTE:if α → ε,then ε is FIRST(α)
exam.
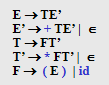
FIRST(E)=FIRST(TE')=FIRST(T)=FIRST(FT')=FIRST(F)={ ( , id }
FIRST(E')=FIRST(+TE')|FIRST(ε)={ + , ε }
FIRST(T)=FIRST(FT')=FIRST(F)={ ( , id }
FIRST(T')={ * , ε }
FIRST(F)={ ( , id }

-
If S is the start symbol : $ is in FOLLOW(S)
-
If A → αBβ is a production rule : everything in FIRST(β) is FOLLOW(B) except ε
-
If ( A→ αB is a production rule ) or ( A → αBβ is a production rule and ε is in FIRST(β) ) : everything in FOLLOW(A) is in FOLLOW(B).
exam.
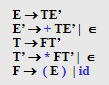
FOLLOW(E) = { ), $ }
FOLLOW(E’) = { ), $ }
FOLLOW(T) = { +, ), $ }
FOLLOW(T’) = { +, ), $ }
FOLLOW(F) = {*, +, ), $ }
构建parsing table 需要分几种情况:
1. 对于每一条分解开的产生式 A → α 重复步骤2&3
2. 如果a in FIRST(α),将A → α添加进M[A,a]
3. 如果ε in FIRST(α),将A → α添加进M[A,b](b是FOLLOW(A)中的所有终结符)
4. 所有没有定义的entries都是errors
exam.



六、 parsing过程
我们回到最开始的一张图:
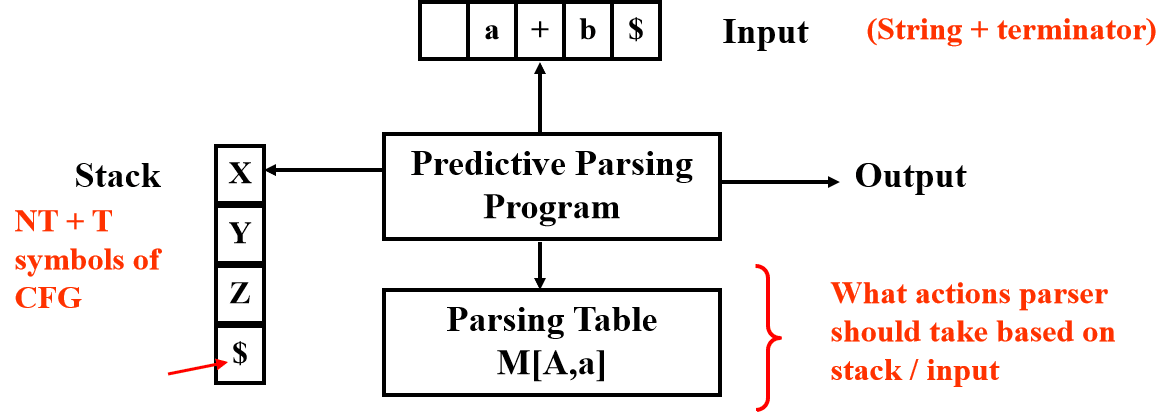
我们将X作为栈顶,a作为current input
分析规则:
1. 当X=a=$ ,终止,accept——success
2. 当X=a≠$,pop X off stack, advance input, 跳转到步骤1
3. 当X是非终结符,查表M[X,a],如果是error:call recovery routine处理;如果是产生式,即M[X,a]={X -> UVW}, pop X, push W,V,U(这里注意是倒序插入stack,因为先进后出),不要前进input。
比如本例子
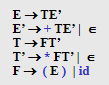

parsing过程:

手写过程就是这样啦:

七、 消除ambiguity
为什么要消除ambiguity——二义性?我们看下面的例子:
stmt -> if expr then stmt | if expr then stmt else stmt | other (any other statement)
简单的语法树是这样的:
general rule:每一个else都要和前面的then相match。
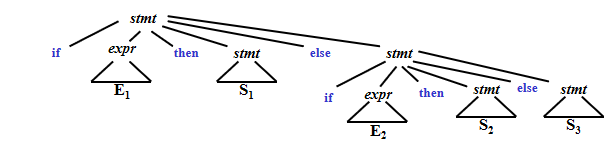
那么如果程序语句是 if E1 then if E2 then S1 else S2

上面两种分析分别对应于下面两种形式的语法树:

出于一般的语法规则,我们更偏向第二种语法树,所以我们需要消除第一种分析带来的影响,我们修改语法规则为下:
stmt -> matchedstmt
| unmatchedstmt matchedstmt -> if expr then matchedstmt else matchedstmt
| otherstmts unmatchedstmt -> if expr then stmt
| if expr then matchedstmt else unmatchedstmt
general rule: 每一个else和上一个最近的没有matched的then相match。
1. 左因式分解LEFT-FACTORING:
基本思想是,当不清楚使用两个替代产生式中的哪一个来扩展非终结符A时,我们可以重写A产生式来推迟决策,直到我们看到足够的输入以做出正确的选择为止 :
比如 A->αβ1 | αβ2
转换成 A->αA'
A'-> A->β1 | β2
2. 消除左递归LEFT-RECURSION:

exam.

八、 源码——内部含有注释
包括非终结符的语法树生成,first集生成,follow集生成,parsing table生成,stack parsing分析过程。
文法由空格间隔,自定义于grammar.txt中;程序语句存于program.txt中。
详情——>我的GitHub->biubiu


