2020-12-9 and 2020-12-10

2020upc第二十五场组队训练

问题 C: Dessert Café时间限制: 1 Sec 内存限制: 128 MB
提交 状态

题目描述

Kim, who wishes to start a business, is trying to open a dessert cafe he has been preparing after graduating from college. The road network in the town where Kim lives forms a tree structure, that is, a connected acyclic graph as shown in the figure below. There are n candidate sites for a dessert café in the town. In the figure below, a circle represents a candidate site for a dessert café, a line segment between two candidate sites represents a road, and the value labeled on a line segment represents the length of a road.

There are k apartment complexes in this town, so he wants his dessert café to be located as close as possible to an apartment complex. In above figure, there are three apartment complexes which are located to the candidate sites labeled by A, B, and C. Considering the competitiveness and profitability, he thinks that a candidate site satisfying the following condition is a good place.

Let d(x, y) be the length of the shortest path on a road network between two candidate sites x and y. A candidate site p is a good place if there exists a candidate site z where an apartment complex is located such that d(p, z) < d(q, z) for each candidate site q (≠ p).

In above figure, candidate sites 2, 4, 5, 6, 8, and 9 are good places. More specifically, for example, candidate 6 is a good place because it is closer to apartment complex B than any other candidate sites except for candidate 5, and is closer to apartment complex A than candidate 5. That is, there exists apartment complex B on candidate 5 satisfying d(6, 5) < d(q, 5) for q ∈ {1, 2, 3, 4, 7, 8, 9}, and there exists apartment complex A on candidate 2 satisfying d(6, 2) < d(5, 2). Candidate 7 is not a good place because none of apartment complexes are closer than candidate 6.

Given the information on candidate sites and apartment complexes in the town, write a program to output the number of good places.

输入

Your program is to read from standard input. The input starts with a line containing two integers, n and k (3 ≤ n ≤ 100,000 , 1 ≤ k ≤ n), where n is the number of candidate sites and k is the number of apartment complexes. The candidate sites are numbered from 1 to n. In the following n − 1 lines, each line contains three integers, i, j, and w (1 ≤ i,j ≤ n, 1 ≤ w ≤ 1,000), where i and j are candidate sites and w is the length of the road between i and j. The last line contains k integers which represent the locations of apartment complexes in the town.

输出

Your program is to write to standard output. Print exactly one line. The line should contain the number of good places.

样例输入 [Copy](javascript:CopyToClipboard($('#sampleinput').text()))

【样例1】
9 3
1 2 8
2 4 7
4 3 6
4 6 4
5 6 3
6 7 2
6 9 5
9 8 6
2 5 8
【样例2】
4 4
1 2 1
1 3 1
1 4 1
2 4 1 3

样例输出 [Copy](javascript:CopyToClipboard($('#sampleoutput').text()))

【样例1】
6
【样例2】
4

换根dp，发现k个点，两两之间路径上的点到k个点的长度和是一样的，并且还是最短的，裸的换根dp

/*
 *@author spnooyseed
 */
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 2e5 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
int e[N] , ne[N] , w[N] , h[N] , idx , n , m , vis[N] ;
void add(int a , int b , int c) {
  e[idx] = b , ne[idx] = h[a] , w[idx] = c , h[a] = idx ++ ;
}
ll dp[N] ;
void dfs(int u , int f){
  for(int i = h[u] ; ~i ; i = ne[i]) {
    int v = e[i] ;
    if(v == f) continue ;
    dfs(v , u) ;
    if(dp[v] || vis[v])
      dp[u] += dp[v] + w[i] ;
  }
  return ;
}
void dfs1(int u , int f , ll sum) {
  dp[u] += sum ;
  for(int i = h[u] ; ~i ; i = ne[i]) {
    int v = e[i] ;
    if(v == f) continue ;
    ll x = dp[u] - dp[v] - w[i] ;
    ll res = x == 0 ? (vis[u] ? w[i] : 0 ) : x + w[i] ;
    if(dp[v] || vis[v])
      dfs1(v , u , res) ;
  }
}
int work()
{
  scanf("%d%d" , &n , &m) ;
  memset(h , -1 , sizeof h) ;
  for(int i = 1; i < n ;i ++ ) {
    int a , b , c ;
    scanf("%d%d%d" , &a , &b , &c) ;
    add(a , b , c) , add(b , a , c) ;
  }
  int res , ans = 0 ;
  for(int i = 1; i <= m ;i ++ ) {
    int x ;
    scanf("%d" , &x) ;
    res = x ;
    vis[x] = 1;
  }
  if(m == 1) {
    return 0 * puts("1") ;
  }
  dfs(1 , 0) ;
  dfs1(1 , 0 , 0) ;
  for(int i = 1; i <= n ;i ++ )
   if(dp[i] == dp[res]) ans ++ ;
  cout << ans << "\n" ;
  return 0 ;
}
int main()
{
    // freopen("C://Users//spnooyseed//Desktop//27.in" , "r" , stdin) ;
  //   freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;
 
  work() ;
  return 0 ;
}
/*
9 1
1 2 8
2 4 7
4 3 6
4 6 4
5 6 3
6 7 2
6 9 5
9 8 6
2
*/

问题 L: Two Buildings时间限制: 1 Sec 内存限制: 512 MB
提交 状态

题目描述

There are n buildings along a horizontal street. The buildings are next to each other along the street, and the i-th building from left to right has width 1 and height hi. Among the n buildings, we are to find two buildings, say the i-th building and j-th building with i < j, such that (hi + hj) × (j − i) is maximized.

For example, the right figure shows 5 buildings, with heights 1, 3, 2, 5, 4, from left to right. If we choose the first 2 buildings, then we get (1 + 3) × (2 − 1) = 4. If we choose the first and fifth buildings, then we (1 + 4) × (5 − 1) = 20. The maximum value is achieved by the second and fifth buildings with heights 3 and 4, respectively: (3 + 4) × (5 − 2) = 21.

Write a program that, given a sequence of building heights, prints max1≤i<j≤n(hi + hj) × (j − i).

输入

Your program is to read from standard input. The input starts with a line containing an integer n (2 ≤ n ≤ 1,000,000), where n is the number of buildings. The buildings are numbered 1 to n from left to right. The second line contains the heights of n buildings separated by a space such that the i-th number is the height hi of the i-th building (1 ≤ hi ≤ 1,000,000).

输出

our program is to write to standard output. Print exactly one line. The line should contain max1≤i<j≤n(hi + hj) × (j − i).

样例输入 [Copy](javascript:CopyToClipboard($('#sampleinput').text()))

【样例1】
5
1 3 2 5 4
【样例2】
5
8 3 6 3 1

样例输出 [Copy](javascript:CopyToClipboard($('#sampleoutput').text()))

【样例1】
21
【样例2】
36

提交状态

2017年icpc WF原题D题稍微改了改，改了一个符号，不讲武德。

/*
 *@author spnooyseed
 */
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<ll , ll> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
PII a[N] , b[N] , c[N] ;
int n , m ;
ll check(int x , int y) {
  if(a[x].x > b[y].x && a[x].y > b[y].y) return 0 ;
  return 1ll * (b[y].x - a[x].x) * (b[y].y - a[x].y) ;
}
ll merge_sort(int L , int R , int l , int r) {
  if(L > R || l > r) return 0 ;
  int mid = L + R >> 1 ;
  int pos = l ;
  ll ans = 0 ;
  for(int i = l ;i <= r ;i ++ )
    if(check(mid , i) > check(mid , pos)) pos = i , ans = check(mid , i) ;
  return max({merge_sort(L , mid - 1 , l , pos) , merge_sort(mid + 1 , R , pos  , r) , check(mid , pos)});
}
bool cmp(PII a , PII b) {
  if(a.y != b.y) return a.y < b.y ;
  return a.x < b.x ;
}
int work()
{
  scanf("%d" , &n) ;
  m = n ;
  for(int i = 1 , x ; i <= n ;i ++ ) {
    scanf("%d" , &x) ;
    a[i] = {-x , i} ;
    b[i] = {x , i} ;
  }
  int idx1 = 0 ;
  sort(a + 1 , a + n + 1 , cmp) ;
  for(int i = 1; i <= n ;i ++ ) {
    if(!idx1 || a[idx1].y != a[i].y) a[++ idx1] = a[i] ;
  }
  n = 0 ;
  for(int i = 1; i <= idx1 ;i ++ )
    if(!n || a[i].x < a[n].x) a[++ n] = a[i] ;
  idx1 = 0 ;
  sort(b + 1 , b + m + 1 , cmp) ;
  for(int i = 1; i <= m ;i ++ ) {
    if(!idx1 || b[idx1].y != b[i].y) b[++ idx1] = b[i] ;
    else b[idx1] = b[i] ;
  }
  m = 0 ;
  for(int i = idx1 ; i >= 1 ;i -- ) {
      if(!m || c[m].x < b[i].x) c[++ m] = b[i] ;
  }
  reverse(c + 1 , c + m + 1) ;
  for(int i = 1; i <= m ;i ++ ) b[i] = c[i] ;
  ll ans = merge_sort(1 , n , 1 , m) ;
  cout << ans << "\n" ;
  return 0 ;
}
int main()
{
    // freopen("C://Users//spnooyseed//Desktop//in.txt" , "r" , stdin) ;
  //   freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;
  work() ;
  return 0 ;
}
/*
*/
 

链接：https://ac.nowcoder.com/acm/problem/214460
来源：牛客网

Triangle Numbers

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

三角形是由同一平面内不在同一直线上的三条线段'首尾'顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角形（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

定义 "三角形"数：如果一个十进制正整数，可以从它的数位中取出三个数字a,b,c,能构成合法的三角形，则称该正整数为"三角形"数。

比如正整数345就是一个"三角形"数，3，4，5分别作为三角形的三条边，组成了一个（直角）三角形。

比如正整数123不是"三角形"数，因为1，2，3三条边无法构成合法的三角形。

现给定区间[A,B]，求区间内"三角形"数的个数。

输入描述:

第一行输入一个整数T代表T组案例


接下来T行，每行两个正整数 A,B


(T≤1000,1≤A≤B≤109)(T \leq 1000, 1 \leq A \leq B \leq 10^9)(T≤1000,1≤A≤B≤109)

输出描述:

输出T行，每一行表示对应区间内的 "三角形"数的个数。

示例1

输入

[复制](javascript:void(0)😉

2
345 345
1 99

输出

[复制](javascript:void(0)😉

1
0

数位dp，难点在于怎么判断一个数是否合法，可以状态压缩，用三进制即可，如果第i位上有3个，那么就符合条件，或者两边之和大于第三边，暴力判断

/*
 *@author spnooyseed
 */
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
int a[N] , cnt , dp[20][40000][2] , pw[N] ;
int get(int s , int x) {
  return (s % pw[x + 1]) / pw[x] ;
}
bool check(int s) {
  int ans = 0 ;
  vector<int> v ;
  for(int i = 1 ;i <= 9 ;i ++ ) {
    int res = get(s , i) ;
    if(res == 3) return true ;
    ans += res ;
    for(int j = 1; j <= res ;j ++ ) v.pb(i) ;
  }
  if(v.size() < 3) return false ;
  for(int i = 1; i < v.size() - 1 ;i ++ ) {
    if(v[i -1 ] + v[i] > v[i + 1]) return true ;
  }
  return false ;
}
int dfs(int u , int s , int ok , int limit) {
  if(!u) return ok || check(s) ;
  if(!limit && dp[u][s][ok] != -1) return dp[u][s][ok] ;
  int end = limit ? a[u] : 9 , ans = 0 ;
  for(int i = 0 ;i <= end ;i ++ ) {
    if(i == 0) ans += dfs(u - 1 , s , ok , limit && i == end) ;
    else {
      int res = get(s , i) ;
      if(res == 2) ans += dfs(u - 1 , s + pw[i] , 1 , limit && i == end) ;
      else ans += dfs(u - 1 , s + pw[i] , ok , limit && i == end) ;
    }
  }
  if(!limit) dp[u][s][ok] = ans ;
  return ans ;
}
int solve(int n) {
  cnt = 0 ;
  while(n) a[++ cnt] = n % 10 , n /= 10 ;
  return dfs(cnt , 0 , 0  ,1) ;
}
int work()
{
  int l , r ;
  scanf("%d%d" , &l , &r) ;
  cout << solve(r) - solve(l - 1) << "\n" ;
  return 0 ;
}
int main()
{
  //   freopen("C://Users//spnooyseed//Desktop//in.txt" , "r" , stdin) ;
  //   freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;
  int n  ;
  pw[0] = 1 ;
  memset(dp , -1 , sizeof dp) ;
  for(int i = 1; i <= 10 ;i ++ ) pw[i] = pw[i - 1] * 3 ;
  scanf("%d" , &n) ;
  while(n -- )
  work() ;
  return 0 ;
}
/*
*/

codeforces 1348F

F. Phoenix and Memory

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Phoenix is trying to take a photo of his nn friends with labels 1,2,…,n1,2,…,n who are lined up in a row in a special order. But before he can take the photo, his friends get distracted by a duck and mess up their order.

Now, Phoenix must restore the order but he doesn't remember completely! He only remembers that the ii-th friend from the left had a label between aiai and bibi inclusive. Does there exist a unique way to order his friends based of his memory?

Input

The first line contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of friends.

The ii-th of the next nn lines contain two integers aiai and bibi (1≤ai≤bi≤n1≤ai≤bi≤n) — Phoenix's memory of the ii-th position from the left.

It is guaranteed that Phoenix's memory is valid so there is at least one valid ordering.

Output

If Phoenix can reorder his friends in a unique order, print YES followed by nn integers — the ii-th integer should be the label of the ii-th friend from the left.

Otherwise, print NO. Then, print any two distinct valid orderings on the following two lines. If are multiple solutions, print any.

Examples

input

Copy

4
4 4
1 3
2 4
3 4

output

Copy

YES
4 1 2 3 

input

Copy

4
1 3
2 4
3 4
2 3

output

Copy

NO
1 3 4 2 
1 2 4 3 

/*
 *@author spnooyseed
 */
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
int val[N] , p[N] , n , L[N] , R[N] ;
struct node {
  int l , r , id ;
  bool operator<(const node &a) const {
    if(l != a.l)
      return l < a.l ;
    return r < a.r ;
  }
}e[N];
int sum[N * 4] ;
void up(int rt) {
  sum[rt] = sum[ls] + sum[rs] ;
}
void update(int rt , int l , int r , int pos , int k) {
  if(l == r) {
    sum[rt] += k ;
    return ;
  }
  int mid = l + r >> 1 ;
  if(pos <= mid) update(ls , l , mid , pos , k) ;
  else update(rs , mid + 1 , r  , pos , k) ;
  up(rt) ;
}
int ask(int rt , int l , int r , int ql , int qr) {
  if(l == r) {
    if(sum[rt])
      return l ;
    return 0 ;
  }
  int ans = 0 , mid = l + r >> 1 ;
  if(ql <= mid && sum[ls]) ans = ask(ls , l , mid , ql , qr) ;
  if(qr > mid && sum[rs] && !ans) ans = ask(rs , mid + 1 , r , ql , qr) ;
  return ans ;
}
int work()
{
  scanf("%d" , &n) ;
  for(int i = 1; i <= n ;i ++ ) {
    scanf("%d%d" , &L[i] , &R[i]) ;
    e[i] = {L[i] , R[i] , i} ;
  }
  sort(e + 1 , e + n + 1) ;
  set<PII> s ;
  for(int i = 1 , j = 1; i <= n ;i ++ ) {
    while(j <= n && e[j].l == i) s.insert({e[j].r , e[j].id}) , j ++ ;
    p[i] = (*s.begin()).y ;
    val[p[i]] = i ;
    s.erase(s.begin()) ;
  }
  for(int i = 1 , j = 1 ; i <= n ;i ++ ) {
    int id = p[i] ;
    while(j <= n && e[j].l == i) update(1 , 1 , n , val[e[j].id] , 1) , j ++ ;
    update(1 , 1 , n , val[id] , -1) ;
    int ans = ask(1 ,1 , n , L[id] , R[id]) ;
    if(ans) {
      puts("NO") ;
      for(int i = 1; i <= n ;i ++ ) cout << val[i] << " " ;
      puts("") ;
      swap(val[id] , val[p[ans]]) ;
      for(int i = 1; i <= n ;i ++ ) cout << val[i] << " " ;
      puts("") ;
      return 0 ;
    }
  }
  puts("YES") ;
  for(int i = 1; i <= n ;i ++ )
   cout << val[i] << " " ;
  puts("") ;
  return 0 ;
}
int main()
{
  //   freopen("C://Users//spnooyseed//Desktop//in.txt" , "r" , stdin) ;
  //   freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;
  work() ;
  return 0 ;
}
/*
*/

codeforces 1380F

F. Strange Addition

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let aa and bb be some non-negative integers. Let's define strange addition of aa and bb as following:

1. write down the numbers one under another and align them by their least significant digit;
2. add them up digit by digit and concatenate the respective sums together.

Assume that both numbers have an infinite number of leading zeros.

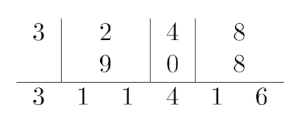
For example, let's take a look at a strange addition of numbers 32483248 and 908908:

You are given a string cc, consisting of nn digits from 00 to 99. You are also given mm updates of form:

• x dx d — replace the digit at the xx-th position of cc with a digit dd.

Note that string cc might have leading zeros at any point of time.

After each update print the number of pairs (a,b)(a,b) such that both aa and bb are non-negative integers and the result of a strange addition of aa and bb is equal to cc.

Note that the numbers of pairs can be quite large, so print them modulo 998244353998244353.

Input

The first line contains two integers nn and mm (1≤n,m≤5⋅1051≤n,m≤5⋅105) — the length of the number cc and the number of updates.

The second line contains a string cc, consisting of exactly nn digits from 00 to 99.

Each of the next mm lines contains two integers xx and dd (1≤x≤n1≤x≤n, 0≤d≤90≤d≤9) — the descriptions of updates.

Output

Print mm integers — the ii-th value should be equal to the number of pairs (a,b)(a,b) such that both aa and bb are non-negative integers and the result of a strange addition of aa and bb is equal to cc after ii updates are applied.

Note that the numbers of pairs can be quite large, so print them modulo 998244353998244353.

Example

input

Copy

2 3
14
2 4
2 1
1 0

output

Copy

15
12
2

Note

After the first update cc is equal to 1414. The pairs that sum up to 1414 are: (0,14)(0,14), (1,13)(1,13), (2,12)(2,12), (3,11)(3,11), (4,10)(4,10), (5,9)(5,9), (6,8)(6,8), (7,7)(7,7), (8,6)(8,6), (9,5)(9,5), (10,4)(10,4), (11,3)(11,3), (12,2)(12,2), (13,1)(13,1), (14,0)(14,0).

After the second update cc is equal to 1111.

After the third update cc is equal to 0101.

可以先将这个东西换成dp形式，然后再写成矩阵形式，最后线段树维护。

/*
 *@author spnooyseed
 */
#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#pragma GCC optimize(3 , "Ofast" , "inline")
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization("unroll-loops")
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <map>
#include <list>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <stack>
#include <set>
#include <bitset>
#include <deque>
using namespace std ;
#define ios ios::sync_with_stdio(false) , cin.tie(0)
#define x first
#define y second
#define pb push_back
#define ls rt << 1
#define rs rt << 1 | 1
typedef long long ll ;
const double esp = 1e-6 , pi = acos(-1) ;
typedef pair<int , int> PII ;
const int N = 1e6 + 10 , INF = 0x3f3f3f3f , mod = 998244353 ;
int v[100] , a[N] , b[N] ;
char s[N] ;
struct node {
  ll a[2][2] ;
}t[N * 4];
node muti(node b , node a) {
  node c ;
  for(int i = 0 ;i < 2 ;i ++ )
   for(int j = 0 ;j < 2 ; j ++ )
    c.a[i][j] = 0 ;
  for(int k = 0 ;k < 2; k ++ )
   for(int i = 0 ;i < 2; i ++ )
    for(int j = 0 ;j < 2; j ++ )
     c.a[i][j] = (c.a[i][j] + a.a[i][k] * b.a[k][j]) % mod ;
  return c ;
}
void up(int rt) {
  t[rt] = muti(t[ls] , t[rs]) ;
}
void build(int rt , int l , int r) {
  if(l == r) {
    t[rt].a[0][0] = v[a[l]] ;
    t[rt].a[0][1] = a[l - 1] == 1 ? v[b[l]] : 0 ;
    t[rt].a[1][0] = 1 ;
    t[rt].a[1][1] = 0 ;
    return ;
  }
  int mid = l + r >> 1 ;
  build(ls , l , mid) ;
  build(rs , mid + 1 , r) ;
  up(rt) ;
  return ;
}
void update(int rt , int l , int r , int pos) {
  if(l == r) {
    t[rt].a[0][0] = v[a[l]] ;
    t[rt].a[0][1] = a[l - 1] == 1 ? v[b[l]] : 0 ;
    t[rt].a[1][0] = 1 ;
    t[rt].a[1][1] = 0 ;
    return ;
  }
  int mid = l + r >> 1 ;
  if(pos <= mid) update(ls , l , mid , pos) ;
  else update(rs , mid + 1 , r , pos) ;
  up(rt) ;
  return ;
}
int work()
{
  for(int i = 0 ; i <= 9 ;i ++ ) v[i] = i + 1 ;
  for(int i = 10 ;i < 19 ;i ++ ) v[i] = 19 - i ;
  int n , m ;
  scanf("%d%d%s" , &n , &m , s + 1) ;
  for(int i = 1; i <= n ;i ++ ) a[i] = s[i] - '0' ;
  for(int i = 2 ;i <= n ;i ++ ) b[i] = a[i - 1] * 10 + a[i] ;
  build(1 , 1 , n) ;
  for(int i = 1; i <= m ;i ++ ) {
    int x , y ;
    scanf("%d%d" , &x , &y) ;
    a[x] = y ;
    b[x] = a[x - 1] * 10 + a[x] ;
    b[x + 1] = a[x] * 10 + a[x + 1] ;
    update(1 , 1 , n , x) ;
    if(x + 1 <= n) update(1 , 1 , n , x + 1) ;
    printf("%lld\n" , t[1].a[0][0]) ;
  }
  return 0 ;
}
int main()
{
  //   freopen("C://Users//spnooyseed//Desktop//in.txt" , "r" , stdin) ;
  //   freopen("C://Users//spnooyseed//Desktop//out.txt" , "w" , stdout) ;

  work() ;
  return 0 ;
}
/*
*/