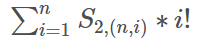第二类斯特灵数

hdu 2643
最近在Teddy的家乡举办了一场名为“Cow Year Blow Cow”的比赛.N竞争对手参加了比赛。比赛非常紧张，排名正在发生变化。
现在的问题是：
竞争者可以在竞争中排名多少种不同的方式，从而允许联系的可能性。
因为答案非常大，你可以输出答案MOD 20090126.
以下是N = 2时的方法：
P1 <P2
P2 <P1
P1 = P2

输入
第一行将包含一个T，然后是T个案例。
每种情况只包含一个整数N（N <= 100），表示人数。

产量
一个整数pey线代表答案MOD 20090126。

样本输入
2
2
3

样本输出
3
13

把一个包含n个元素的集合分成k个非空子集的方法数：
初始值：
S2(n,0)=0,S2(n,k)=0(n<k)S2(n,0)=0,S2(n,k)=0(n<k)
S2(n,1)=S2(n,n)=1S2(n,1)=S2(n,n)=1
递推式：
S2(n,k)=S2(n−1,k−1)+S2(n−1,k)∗kS2(n,k)=S2(n−1,k−1)+S2(n−1,k)∗k
考虑第n个元素，如果它自成一个集合，那么前n-1个元素构成k-1个集合，就是S(n,k),如果它不是自成集合，那么前面n-1个元素构成k个集合，再把第n个元素加到任意一个集合中，共k种方案。
题目大意：
n位选手参加比赛，每个选手有一个排名，有可能有并列，那么排名情况有多少种可能？
n位选手可以放到1个集合，两个集合。。。。n个集合，因为每个集合对应的是名次，所以集合是区分的。
那么对于n个选手，可以选择的方案数：

#include <bits/stdc++.h>

using namespace std;
const int mod = 20090126;
const int MAXN = 100+5;
int n;
int s2[MAXN][MAXN];
int fac[MAXN];
void get_s2()
{
    fac[0] = 1;
    for(int i = 1; i <= 100; ++i)fac[i] = (long long)fac[i-1]*i%mod;
    for(int i = 1; i <= 100; ++i)
    {
        s2[i][1] = s2[i][i] = 1;
        for(int j = 2; j < i; ++j)
        {
            s2[i][j] = (s2[i-1][j-1] + (long long)j*s2[i-1][j]%mod)%mod;
        }
    }
}

int main()
{
    get_s2();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        int ans = 0;
        for(int i = 1; i <= n; ++i)ans = (ans+(long long)fac[i]*s2[n][i]%mod)%mod;
        printf("%d\n",ans);
    }
    return 0;
}