前缀和

题目

LeetCode	力扣	难度
303. Range Sum Query - Immutable	303. 区域和检索 - 数组不可变	🟢
304. Range Sum Query 2D - Immutable	304. 二维区域和检索 - 矩阵不可变	🟠
-同	剑指 Offer II 013. 二维子矩阵的和	🟠

-----------

303. 区域和检索 - 数组不可变

我的答案

1、题目理解
前缀和只差
2、注意事项
前缀和 preSum[1] = 0+num[0]，即preSum[i+1]包含num[i]
向量动态扩展大小的方法 resize

3、我的代码

using namespace std;
class NumArray {
    vector<int> presum;
public:
    NumArray(vector<int>& nums) {
        presum.resize(nums.size() + 1, 0);
        presum[0] = 0;
        for (int i = 0; i < nums.size(); ++i) {
            presum[i + 1] = presum[i] + nums[i];
        }
    }

    int sumRange(int left, int right) {
        
        return presum[right+1] - presum[left];
    }
};

python 版本

class NumArray:

    def __init__(self, nums: List[int]):
        self.sums = [0]
        _sums = self.sums

        for num in nums:
            _sums.append(_sums[-1] + num)

    def sumRange(self, i: int, j: int) -> int:
        _sums = self.sums
        return _sums[j + 1] - _sums[i]

作者：力扣官方题解
链接：https://leetcode.cn/problems/range-sum-query-immutable/solutions/627052/qu-yu-he-jian-suo-shu-zu-bu-ke-bian-by-l-px41/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

304. 二维区域和检索 - 矩阵不可变

我的答案：多组一维前缀和之和

1、题目理解
多组前缀和之差
2、注意事项
向量动态扩展大小的方法 resize，最外层也需要扩一次
3、我的思路

using namespace std;

class NumMatrix {
    vector<vector<int>> presum;
public:
    NumMatrix(vector<vector<int>> &matrix) {
        presum.resize(matrix.size());
        for (int j = 0; j < matrix.size(); ++j) {
            presum[j].resize(matrix[j].size() + 1, 0);
            presum[j][0] = 0;
            for (int i = 0; i < matrix[j].size(); ++i) {
                presum[j][i + 1] = presum[j][i] + matrix[j][i];
            }
        }

    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; ++i) {
            sum += presum[i][col2 + 1] - presum[i][col1];
        }
        return sum;
    }
};

二维前缀和解法

二维前缀和

class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(matrix):
            for j, x in enumerate(row):
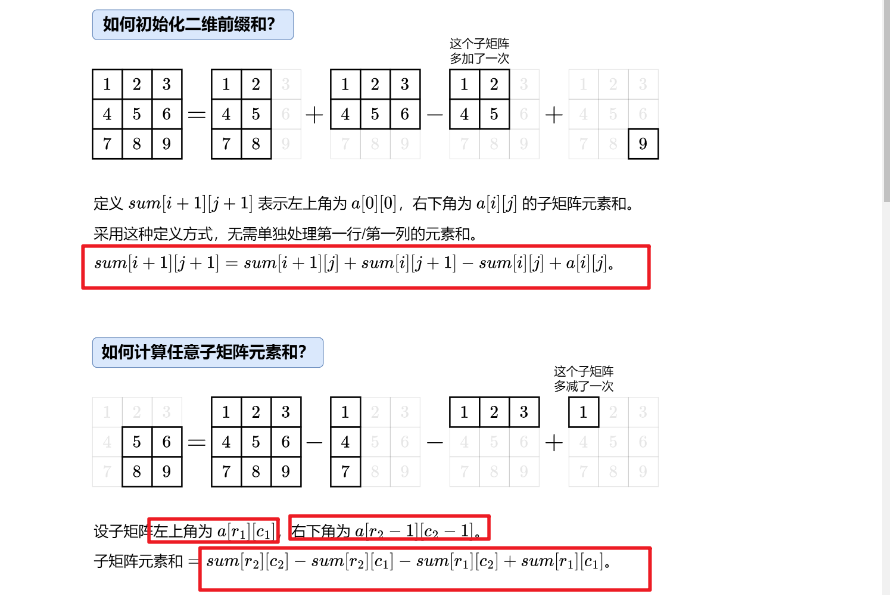
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + x
        self.s = s

    # 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
    def sumRegion(self, r1: int, c1: int, r2: int, c2: int) -> int:
        return self.s[r2 + 1][c2 + 1] - self.s[r2 + 1][c1] - self.s[r1][c2 + 1] + self.s[r1][c1]

作者：灵茶山艾府
链接：https://leetcode.cn/problems/range-sum-query-2d-immutable/solutions/2667331/tu-jie-yi-zhang-tu-miao-dong-er-wei-qian-84qp/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。