11种排序算法（Python实现）
10种排序算法（Python实现）
冒泡排序
1、 两重循环，每次都将一个点移动到最终位置
def BubbleSort(lst):
n=len(lst)
if n<=1:
return lst
for i in range (0,n):
for j in range(0,n-i-1): # 每轮确定一个点的最终位置
if lst[j]>lst[j+1]:
(lst[j],lst[j+1])=(lst[j+1],lst[j])
return lst
x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in y:
arr.append(int(i))
arr=BubbleSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
print(i,end=' ')
快速排序
快排具体算法执行流程如下：https://www.cnblogs.com/MOBIN/p/4681369.html
1、每次都会确定基准值的最终位置
2、快排使用到了，分页和递归
def QuickSort(lst):
# 此函数完成分区操作，并且返回该元素的最终位置
def partition(arr, left, right):
# 执行快排的过程
key = left # 使用第一个数为基准数
while left < right:
# 如果列表后边的数,比基准数大或相等,则前移一位直到有比基准数小的数出现
while left < right and arr[right] >= arr[key]:
right -= 1
# 如果列表前边的数,比基准数小或相等,则后移一位直到有比基准数大的数出现
while left < right and arr[left] <= arr[key]:
left += 1
# 此时已找到一个比基准大的书，和一个比基准小的数，将他们互换位置
(arr[left], arr[right]) = (arr[right], arr[left])
# 当从两边分别逼近，直到两个位置相等时结束，将左边小的同基准进行交换
(arr[left], arr[key]) = (arr[key], arr[left])
# 返回目前基准所在位置的索引
return left
def quicksort(arr, left, right):
if left >= right:
return
# 获取一个元素的最终位置
mid = partition(arr, left, right)
# 递归调用
# print(arr)
quicksort(arr, left, mid - 1)
quicksort(arr, mid + 1, right)
# 主函数
n = len(lst)
if n <= 1:
return lst
quicksort(lst, 0, n - 1)
return lst
print("<<< Quick Sort >>>")
x = input("请输入待排序数列：\n")
y = x.split()
arr = []
for i in y:
arr.append(int(i))
arr = QuickSort(arr)
# print(arr)
print("数列按序排列如下：")
for i in arr:
print(i, end=' ')
插入排序（有序+无序）
插入排序算法流程：1 从第二个元素开始，第一个默认为有序，将取出的元素放到前面有序的队列中，放的时候是平移。n2时间复杂度。注意这里比较的时候顺便挪动，因此是两重循环
def InsertSort(lst):
n=len(lst)
if n<=1:
return lst
for i in range(1,n):
j=i
target=lst[i] #每次循环的一个待插入的数
while j>0 and target<lst[j-1]: #比较、后移，给target腾位置
lst[j]=lst[j-1]
j=j-1
lst[j]=target #把target插到空位
return lst
x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in y:
arr.append(int(i))
arr=InsertSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
print(i,end=' ')
希尔排序
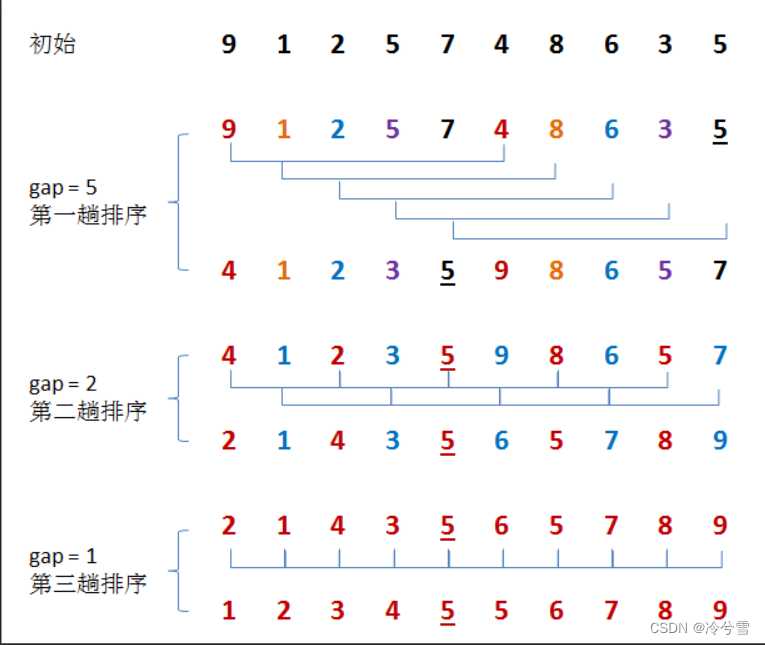
希尔排序的算法流程：
第一遍：分成5组，
第二遍：分成2组，4 3 5 8 5会被进行插入排序
第三遍：gap=1，分成1组，对全部数组进行直接插入排序
def shell_sort(arr):
# 初始化间隔gap
gap = len(arr) // 2
# 开始希尔排序
while gap > 0:
# 遍历所有间隔为gap的元素组
for i in range(gap, len(arr)):
temp = arr[i]
j = i
# 插入排序的思想，对间隔为gap的元素组进行直接插入排序操作
while j - gap >= 0 and temp < arr[j - gap]:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
# 更新间隔
gap //= 2
return arr
# 测试希尔排序函数
example_array = [64, 34, 25, 12, 22, 11, 90]
sorted_array = shell_sort(example_array)
print("排序后的数组：", sorted_array)
堆排序（难）
堆排序（Heap Sort）是一种基于比较的排序算法，它利用堆这种数据结构的特性来进行排序。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子节点的键值或索引总是小于（或者大于）它的父节点。
堆排序算法包括两个主要步骤：
建立堆：将无序数组构造成一个最大堆或最小堆。
逐步提取堆顶元素并恢复堆性质：将堆顶元素与最后一个元素交换，然后减少堆的大小，最后调整剩余元素构成的堆，重复这个过程直到堆的大小为1。
def heapify(arr, n, i):
# 设定最大值索引为i
largest = i
# 左子节点索引为2*i+1
left = 2 * i + 1
# 右子节点索引为2*i+2
right = 2 * i + 2
# 如果左子节点大于根节点
if left < n and arr[i] < arr[left]:
largest = left
# 如果右子节点比最大值还大
if right < n and arr[largest] < arr[right]:
largest = right
# 如果最大值不是根节点
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # 交换
# 递归地定义子堆
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# 构建最大堆
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 一个个从堆顶取出元素
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
return arr
# 测试堆排序函数
example_array = [12, 11, 13, 5, 6, 7]
sorted_array = heap_sort(example_array)
print("排序后的数组：", sorted_array)
归并排序(合并有序序列)
O(nlogn）的时间复杂度，稳定排序
- 把长度为n的输入序列分成两个长度为n/2的子序列；
- 对这两个子序列分别采用归并排序；
- 将两个排序好的子序列合并成一个最终的排序序列（这里一次遍历就行了，合并两个有序序列的复杂度是n）
def MergeSort(lst):
#合并左右子序列函数
def merge(arr,left,mid,right):
temp=[] #中间数组
i=left #左段子序列起始
j=mid+1 #右段子序列起始
while i<=mid and j<=right:
if arr[i]<=arr[j]:
temp.append(arr[i])
i+=1
else:
temp.append(arr[j])
j+=1
while i<=mid:
temp.append(arr[i])
i+=1
while j<=right:
temp.append(arr[j])
j+=1
for i in range(left,right+1): # !注意这里，不能直接arr=temp,他俩大小都不一定一样
arr[i]=temp[i-left]
#递归调用归并排序
def mSort(arr,left,right):
if left>=right:
return
mid=(left+right)//2
mSort(arr,left,mid)
mSort(arr,mid+1,right)
merge(arr,left,mid,right)
n=len(lst)
if n<=1:
return lst
mSort(lst,0,n-1)
return lst
x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in y:
arr.append(int(i))
arr=MergeSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
print(i,end=' ')
计数排序（空间浪费严重）
- 找出待排序的数组中最大和最小的元素；（来建立一个桶）如果这里最大值100，就有100个桶
- 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
- 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
- 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。
def CountSort(lst):
n=len(lst)
num=max(lst)
count=[0]*(num+1)
for i in range(0,n):
count[lst[i]]+=1
arr=[]
for i in range(0,num+1):
for j in range(0,count[i]):
arr.append(i)
return arr
x=input("请输入待排序数列：\n")
y=x.split()
arr=[]
for i in y:
arr.append(int(i))
arr=CountSort(arr)
#print(arr)
print("数列按序排列如下：")
for i in arr:
print(i,end=' ')
桶排序（合并多个有序数组）
1、 先分多个桶（可以直接使用n/10这种方法，桶是有序的）
2、在桶内进行排序（任何排序均可）
import java.util.ArrayList;
import java.util.List;
//微信公众号：bigsai
public class test3 {
public static void main(String[] args) {
int a[]= {1,8,7,44,42,46,38,34,33,17,15,16,27,28,24};
List[] buckets=new ArrayList[5];
for(int i=0;i<buckets.length;i++)//初始化
{
buckets[i]=new ArrayList<Integer>();
}
for(int i=0;i<a.length;i++)//将待排序序列放入对应桶中
{
int index=a[i]/10;//对应的桶号
buckets[index].add(a[i]);
}
for(int i=0;i<buckets.length;i++)//每个桶内进行排序(使用系统自带快排)
{
buckets[i].sort(null);
for(int j=0;j<buckets[i].size();j++)//顺便打印输出
{
System.out.print(buckets[i].get(j)+" ");
}
}
}
}
基数排序（Radix Sort）(多轮桶排)
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前
算法实现：
1、取最大值得到最高位
2、从低位到高位，建立桶依次收集和分散，反复几轮之后就是有序的了
算法图解：
下面这段代码实现的很巧妙
1、取最大值得到最高位
2、从低位到高位，建立桶依次收集和分散，反复几轮之后就是有序的了
def radix(arr):
digit = 0
max_digit = 1
max_value = max(arr)
#找出列表中最大的位数 10^max_digit
while 10**max_digit < max_value:
max_digit = max_digit + 1
while digit < max_digit:
temp = [[] for i in range(10)] # 二维数组,有10个元素 [[],[],[],..[]]
for i in arr:
#求出每一个元素的个、十、百位的值
t = int((i/(10**digit))%10) # 依次取个位 10位 百位
temp[t].append(i)
coll = []
# 将桶里的东西依次倒出来
for bucket in temp:
for i in bucket:
coll.append(i)
arr = coll # 此时coll其实已经排过序了
digit = digit + 1
return arr
选择排序（有序+无序）
选择排序（select sorting）也是一种简单的排序方法。
基本思想为：
第一次从
arr[0]~arr[n-1]中选取最小值，与 arr[0] 交换第二次从
arr[1]~arr[n-1]中选取最小值，与 arr[1] 交换第 i 次从
arr[i-1]~arr[n-1]中选取最小值，与 arr[i-1] 交换依次类图，总共通过
n - 1次，得到一个按排序码从小到大排列的有序序列
def selection_sort(arr):
# 遍历数组中的所有元素
for i in range(len(arr)):
# 将当前位置设为最小值位置
min_index = i
# 从i+1到数组末尾中找到最小元素的索引
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
min_index = j
# 将找到的最小值交换到它应该在的位置
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
# 测试选择排序函数
example_array = [64, 25, 12, 22, 11]
sorted_array = selection_sort(example_array)
print("排序后的数组：", sorted_array)
总结
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面
