分块全家桶
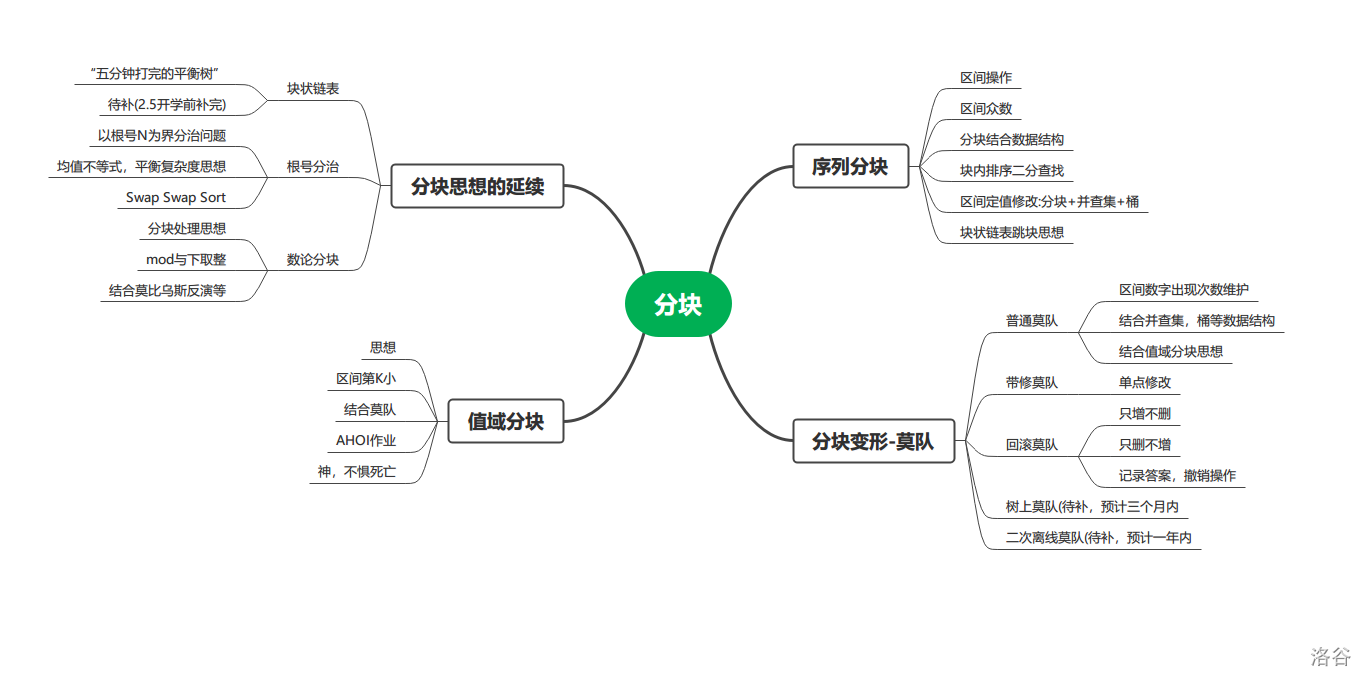
RT,本文探讨一些简单的分块应用,不会涉及太高深的分块知识。
PS:如有错误请不吝赐教,不胜感激
PS:代码仅供参考
PS:更新了Ynoi杂题记
分块
友情提醒:#include<cmath>
望月悲叹的最初分块
分块,优雅的暴力
分块也是同线段树等结构一样,维护区间操作的,不同于线段树和树状数组的是,分块所维护的信息并不需要满足区间可加性,以此,分块可以处理许多线段树等结构不可以处理的问题
简单来说,分块就是将整个序列分为若干个大小相同的块(最后一个可能不同),然后对于每一个块再加以维护,在统计信息时,我们仅仅需要将所需区间\([l,r]\)中所完全包含的块的信息统计,然后对于两端零散的块执行暴力,修改同理
为了平衡复杂度,一般取块长\(block=\sqrt{n}\)
//初始化
block=sqrt(n),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(n,L[i]+block-1);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
举一个简单的例子,分块维护区间加法
我们只需要将其分为块之后对于每一个块建立一个求和数组即可,然后类似线段树的,建立一个懒标记
#include<bits/stdc++.h>
#define int long long
using namespace std;
int sum[1005],a[1000005],lz[1005],pos[1000005],L[1005],R[1005];
int block,siz,n,m;
void init(){
cin>>n>>m;
block=sqrt(n),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(n,L[i]+block-1);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
sum[pos[i]]+=a[i];
}
}
void change(int l,int r,int d){
if(pos[l]==pos[r]){
for(int i=l;i<=r;i++)a[i]+=d,sum[pos[i]]+=d;
return ;
}
for(int i=l;i<=R[pos[l]];i++){
a[i]+=d;sum[pos[i]]+=d;
}
for(int i=L[pos[r]];i<=r;i++){
a[i]+=d;sum[pos[i]]+=d;
}
for(int i=pos[l]+1;i<pos[r];i++){
lz[i]+=d;sum[i]+=(R[i]-L[i]+1)*d;
}
}
void updata(int i){
for(int k=L[i];k<=R[i];k++)a[k]+=lz[i];
lz[i]=0;
}
int ask(int l,int r){
int ans=0;
if(pos[l]==pos[r]){
updata(pos[l]);
for(int i=l;i<=r;i++){
ans+=a[i];
}
return ans;
}
updata(pos[l]);updata(pos[r]);
for(int i=pos[l]+1;i<pos[r];i++)ans+=sum[i];
for(int i=l;i<=R[pos[l]];i++)ans+=a[i];
for(int i=L[pos[r]];i<=r;i++)ans+=a[i];
return ans;
}
signed main(){
ios::sync_with_stdio(false);
init();
while(m--){
int opt,l,r,k;
cin>>opt>>l>>r;
if(opt==1){
cin>>k;change(l,r,k);
}
else cout<<ask(l,r)<<endl;
}
}
洛谷线段树模版的AC记录
下面我们来探讨分块模型的各种扩展
突凿穿刺的进阶分块
蒲公英
静态维护区间众数问题,\(n\le 4\times 10^4,m\le 5\times 10^4\)
既然要维护区间众数,那么我们需要考虑和知晓的肯定是各个区间里各个数的出现的次数
于是进行分块,对于每一个块,求出一个\(sum\)数组,\(sum[i][j]\)表示在前\(i\)个块中数\(j\)的出现次数,下一步,我们需要统计出答案\(mx\)数组,\(mx[i][j]\)表示第\(i\)块到第\(j\)块的区间众数。因为有了\(sum\)数组,我们可以静态的枚举块,若块长为\(\sqrt{n}\),则有\(O(n)\)个区间.
我们的问题就是如何\(O(n\sqrt{n})\)地预处理出\(mx\)了,可以如此设想:假若我们处理出了\(mx[i][j]\),求\(mx[i][j+1]\)的时候,我们可以扫描第\(j+1\)个块,当扫描到数\(x\)的时候,利用\(sum\)数组判断是否可以更新区间众数即可,我们就完成了\(\sqrt{n}\)时间内的状态转移,总计需要\(O(n\sqrt{n})\)的时间
下一步,我们应该考虑如何处理询问
可以采用二次扫描法,即对于区间\([l,r]\)来说,我们可以利用\(mx和sum\),然后对这个大块的两端零散部分,直接用这两个数组进行扫描,对于\(mx\)的更新操作类比预处理时即可,在得出答案之后,再重新倒过来执行一次过程,将修改操作撤销,就可以了。
在实际代码中,为了消去撤销操作,可以单独建立数组\(tot\)处理两端,为了代码的方便懒惰,在统计mx的时候可以建立一个一维数组\(cnt\),在枚举块起点的时候即可进行统计修改
int q,n,m,block,siz,sum[205][40005],vis[40005],a[40005],b[40005],c[40005];
int tot[40005],cnt[40005],last;
struct node {
int num,s;
}p[205][205];
int get(int x){
return x%block==0?x/block:x/block+1;
}
inline void init(){
scanf("%d%d",&n,&m);
block=sqrt(n),siz=n%block==0?n/block:n/block+1;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),c[i]=a[i];
sort(a+1,a+n+1);
int q=unique(a+1,a+n+1)-a-1;
for(int i=1;i<=n;i++){
int pos=lower_bound(a+1,a+q+1,c[i])-a;
b[pos]=c[i];
c[i]=pos;
}
for(int i=1;i<=siz;i++){
memset(cnt,0,sizeof(cnt));
node x;
x.num=x.s=0;
for(int j=i;j<=siz;j++){
for(int k=(j-1)* block+1;k<=min(n,j * block);k++){
cnt[c[k]]++;
if((cnt[c[k]]>x.s)||(cnt[c[k]]==x.s&&c[k]<x.num)){
x.num=c[k];
x.s=cnt[c[k]];
}
}
p[i][j]=x;
}
}
for(int i=1;i<=siz;i++){
for(int j=1;j<=q;j++)sum[i][j]=sum[i-1][j];
for(int j=(i-1)* block+1;j<=min(n,i * block);j++)sum[i][c[j]]++;
}
}
int solve(int l,int r){
int ans=0;
int L=get(l),R=get(r);
if(R-L<=2){//优雅暴力
for(int j=l;j<=r;j++)tot[c[j]]=0;
for(int j=l;j<=r;j++){
tot[c[j]]++;
if(tot[c[j]]>tot[ans]||(tot[c[j]]==tot[ans]&&ans>c[j]))ans=c[j];
}
}
else {
ans=p[L+1][R-1].num;
tot[ans]=0,vis[ans]=0;
for(int j=l;j<=min(n,L * block);j++)tot[c[j]]=0,vis[c[j]]=0;
for(int j=(R-1)* block+1;j<=r;j++)tot[c[j]]=0,vis[c[j]]=0;
for(int j=l;j<=min(n,L * block);j++)tot[c[j]]++;
for(int j=(R-1)* block+1;j<=r;j++)tot[c[j]]++;
int id,mx=0;
for(int j=l;j<=min(n,L * block);j++){
if(!vis[c[j]]){
vis[c[j]]=1;
int val=tot[c[j]]+sum[R-1][c[j]]-sum[L][c[j]];
if(mx < val||(mx==val&&id>c[j]))mx=val,id=c[j];
}
}
for(int j=(R-1)* block+1;j<=r;j++){
if(!vis[c[j]]){
vis[c[j]]=1;
int val=tot[c[j]]+sum[R-1][c[j]]-sum[L][c[j]];
if(mx < val||(mx==val&&id>c[j]))mx=val,id=c[j];
}
}
if(mx>tot[ans]+p[L+1][R-1].s||(mx==tot[ans]+p[L+1][R-1].s&&ans>id))ans=id;
}
last=b[ans];
return last;
}
int main(){
init();
for(int i=1;i<=m;i++){
int l,r;s canf("%d%d",&l,&r);
l=(l+last-1)%n+1;
r=(r+last-1)%n+1;
if(l>r)swap(l,r);
printf("%d\n",solve(l,r));
}
return 0;
}
其实对于本题,还有另外一种方法维护某个区间内某个数的出现次数,也即我门需要的\(cnt\),就是对每一个数开一个\(vector\),;里面存入每一个数在序列中每一次出现的位置(有序),然后对于查询\([l,r]\)中数出现的次数只需要二分查找然后将下标相减即可
值得一说的是,如果本题不强制在线,可考虑莫队解决,复杂度\(O(M\sqrt N)\)
作诗
静态维护区间出现正偶次数的数的个数,强制在线
考虑分块,设\(sum[i,j]\)表示前\(i\)块中数字\(j\)的出现次数。做法显然
设\(ans[l,r]\)表示第\(l\)块到第\(r\)块的答案,做法是:进行递推求解,
- \(ans[l,r]=ans[l,r-1]\)
- 枚举\([L[r],R[r]]\)中的每个数,查询这个数在\([L[l],R[r-1]]\)的出现次数与\([L[l],R[r]]\)的出现次数,分类讨论更新答案(记得只能统计一次,可以通过
vis实现,记得撤销) - 大功告成
对于答案的查询,首先\(Ans=ans[pos[l]+1,pos[r]-1]\)肯定没有任何问题。
然后将在\([l,R[pos[l]]],[L[pos[r]],r]\)中出现过的数在大块\([pos[l]+1,pos[r]-1]\)的出现次数预处理进cnt,然后统计答案就类似于预处理的第2步,具体可以看代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define N 100005
#define M 320
int a[N],vis[N],n,m,c,L[M],R[M],siz,block,ans[M][M],sum[M][N],pos[N],cnt[N];
void init(){
cin>>n>>c>>m;++c;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)a[i]++;
block=sqrt(n),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(n,L[i]+block-1);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
for(int i=1;i<=siz;i++){
for(int j=1;j<=c;j++)sum[i][j]=sum[i-1][j];
for(int j=L[i];j<=R[i];j++)sum[i][a[j]]++;
}
for(int i=1;i<=siz;i++){
for(int j=L[i];j<=R[i];j++){
int k=cnt[a[j]];
if(k&1)ans[i][i]++;
else if(k>0)ans[i][i]--;
cnt[a[j]]++;
}
for(int j=L[i];j<=R[i];j++){
cnt[a[j]]=0;
}
}
for(int i=1;i<=siz;i++){
for(int j=i+1;j<=siz;j++){
ans[i][j]=ans[i][j-1];
for(int k=L[j];k<=R[j];k++){
if(vis[a[k]])continue;
vis[a[k]]=1;
int pre=sum[j-1][a[k]]-sum[i-1][a[k]];
int now=sum[j][a[k]]-sum[j-1][a[k]];
if(!pre){
if(now>0&&now%2==0)ans[i][j]++;
}
else if(pre&1){
if(now&1)ans[i][j]++;
}
else {
if(now&1)ans[i][j]--;
}
}
for(int k=L[j];k<=R[j];k++){
vis[a[k]]=0;
}
}
}
}
int solve(int l,int r){
int Ans=0;
if(pos[l]==pos[r]){
for(int i=l;i<=r;i++){
int k=cnt[a[i]];
if(k&1)Ans++;
else if(k>0)Ans--;
cnt[a[i]]++;
}
for(int i=l;i<=r;i++)cnt[a[i]]=0;
return Ans;
}
Ans=ans[pos[l]+1][pos[r]-1];
for(int i=l;i<=R[pos[l]];i++){
cnt[a[i]]=sum[pos[r]-1][a[i]]-sum[pos[l]][a[i]];
}
for(int i=L[pos[r]];i<=r;i++){
cnt[a[i]]=sum[pos[r]-1][a[i]]-sum[pos[l]][a[i]];
}
for(int i=l;i<=R[pos[l]];i++){
int k=cnt[a[i]];
if(k&1)Ans++;
else if(k>0)Ans--;
cnt[a[i]]++;
}
for(int i=L[pos[r]];i<=r;i++){
int k=cnt[a[i]];
if(k&1)Ans++;
else if(k>0)Ans--;
cnt[a[i]]++;
}
for(int i=l;i<=R[pos[l]];i++){
cnt[a[i]]=0;
}
for(int i=L[pos[r]];i<=r;i++){
cnt[a[i]]=0;
}
return Ans;
}
int main(){
ios::sync_with_stdio(false);
init();
int lst=0;
while(m--){
int l,r;cin>>l>>r;
l=(l+lst)%n+1,r=(r+lst)%n+1;
if(l>r)swap(l,r);
lst=solve(l,r);
cout<<lst<<"\n";
}
}
分块算法还有很多扩展,详见Ynoi
有时候遇到某些较为复杂的问题,甚至可以对分块算法进行扩展,比如先对序列进行分块,然后对于每一个块又进行值域分块
下面是一道分块结合桶与并查集的好题:
星之界
分析:
考虑化简这个可恶的式子
拆开,设\(S\)为前缀和数组
现在我们需要一个维护区间和和区间阶乘积并且支持区间定值修改的数据结构
貌似线段树之类的不行,考虑分块实际上是看见了1e5
统计比较容易,主要难点在于区间定值修改。注意到值域与\(n\)同级,考虑开桶来维护每个值,为了保证复杂度,对于每一个块开一个桶,空间复杂度\(O(N\sqrt N)\),勉强可以承受
但是一个桶只能表示这个值出现的数量,为了维护\(O(N\sqrt N )\)的复杂度,需要更好的工具来维护。
或许可以类比懒标记的思想,延迟修改。那么我们只需要知道每个位置最终表示哪个数即可。
如果把每个桶中的元素看作集合,那么区间定值修改就类似于合并集合,这启发我们联系并查集算法。
那么最初将每个位置看做单独的集合,初始化块的时候将值相同的位置合并成一个集合,为了方便代码,可以选取每个值在块内第一次出现的位置为代表元。
在修改的时候,对于每一个块将表示值\(x\)的集合合并到\(y\)去,注意有可能\(y\)所在集合是空的,此时只需要将代表元的值更改即可。在散块更改的时候,可以直接暴力重置这个块。
核心代码
struct node {
int id, cnt;
}f[S][N];//桶
struct Node {
int sum, mul;
};
int get(int x) {
return x == fa[x] ? x : fa[x] = get(fa[x]);
}
inline void init(int id) {//重置这个块
mul[id] = 1;
sum[id] = 0;
for (re int i = L[id]; i <= R[id]; i++) {
if (f[id][a[i]].id) {
f[id][a[i]].cnt++;
fa[i] = f[id][a[i]].id;
}
else {
f[id][a[i]].id = i;
fa[i] = i;
val[i] = a[i];//val是真实值
f[id][a[i]].cnt = 1;
}
sum[id] += a[i];
mul[id] = 1ll * mul[id] * inv[a[i]] % p;
}
}
inline void clear(int id) {
for (re int i = L[id]; i <= R[id]; i++) {
a[i] = val[get(i)];
f[id][a[i]].cnt = f[id][a[i]].id = 0;
}
for (re int i = L[id]; i <= R[id]; i++) {
fa[i] = 0;
}
}
inline void change_only(int id, int l, int r, int x, int y) {
clear(id);
for (re int i = l; i <= r; i++) {
if (a[i] == x)a[i] = y;
}
init(id);
}
inline void change_all(int id, int x, int y) {
f[id][y].cnt += f[id][x].cnt;
sum[id] -= (x - y) * f[id][x].cnt;
mul[id] = 1ll * mul[id] * power_jc[x][f[id][x].cnt] % p * power_inv[y][f[id][x].cnt] % p;//为了保证复杂度,预处理阶乘及其逆元的幂
if (f[id][y].id == 0)f[id][y].id = f[id][x].id, val[f[id][x].id] = y;
else fa[f[id][x].id] = f[id][y].id;
f[id][x] = { 0,0 };
}
inline void change(int l, int r, int x, int y) {
if (pos[l] == pos[r]) {
change_only(pos[l], l, r, x, y);
return;
}
change_only(pos[l], l, R[pos[l]], x, y);
change_only(pos[r], L[pos[r]], r, x, y);
for (re int i = pos[l] + 1; i < pos[r]; i++)change_all(i, x, y);
}
查询的时候就很简单,将涉及到的积乘上,将和加上
inline Node find_only(int l, int r) {
Node ans = { 0,1 };
for (re int i = l; i <= r; i++) {
ans.sum += val[get(i)];
ans.mul = 1ll * ans.mul * inv[val[get(i)]] % p;
}
return ans;
}
inline Node find_all(int id) {
return { sum[id],mul[id] % p };
}
inline Node merge(Node a, Node b) {
return { a.sum + b.sum,1ll * a.mul * b.mul % p };
}
inline int find(int l, int r) {
if (pos[l] == pos[r]) {
Node ans = find_only(l, r);
return 1ll * jc[ans.sum] * ans.mul % p;
}
Node ans = merge(find_only(l, R[pos[l]]), find_only(L[pos[r]], r));
for (re int i = pos[l] + 1; i < pos[r]; i++) {
ans = merge(ans, find_all(i));
}
return 1ll * jc[ans.sum] * ans.mul % p;
}
预处理的时候就常规预处理,然后处理阶乘逆元,预处理他们的幂保证复杂度(反正空间够),注意逆元得递推求
inline void init() {
jc[1] = inv[1] = 1;
for (re int i = 2; i <= M - 50; i++) {
jc[i] = 1ll * jc[i - 1] * i % p;
inv[i] = p - (1ll * p / (1ll * i) * 1ll * inv[p % i] % p) % p;
}
for (re int i = 2; i <= M - 50; i++) {
inv[i] = 1ll * inv[i - 1] * inv[i] % p;
}
scanf("%d%d", &n, &m);
for (re int i = 1; i <= n; i++)scanf("%d", &a[i]);
block = sqrt(n);
siz = n % block ? n / block + 1 : n / block;
for (re int i = 1; i <= siz; i++) {
L[i] = (i - 1) * block + 1;
R[i] = min(i * block, n);
}
for (re int i = 1; i <= siz; i++) {
for (re int j = L[i]; j <= R[i]; j++) {
pos[j] = i;
}
}
for (re int i = 1; i <= N - 5; i++) {
power_jc[i][0] = power_inv[i][0] = 1;
for (re int j = 1; j <= block; j++) {
power_jc[i][j] = 1ll * power_jc[i][j - 1] * jc[i] % p;
power_inv[i][j] = 1ll * power_inv[i][j - 1] * inv[i] % p;
}
}
for (re int i = 1; i <= siz; i++)init(i);
}
注意有个细节(没注意到就是25pts,调我好久,还是看题解才发现的),当修改时\(x=y\),需要直接跳过不变,因为这会导致\(cnt\)等的值不正确
弹飞绵羊
这紫题水分怕不是一般的大
非常Easy。对序列进行分块,计算出每个点跳出这个块之后在哪个位置,需要跳几次,修改的时候直接暴力重构就行。我觉得看代码就能懂。
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
#define N 250500
int L[N],R[N],pos[N],n,m,block,siz,a[N],cnt[N],sit[N];
void init(){
cin>>n;for(int i=1;i<=n;i++)cin>>a[i];
block=sqrt(n),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(L[i]+block-1,n);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
for(int i=siz;i;--i)
for(int j=R[i];j>=L[i];--j){
if(j+a[j]>R[i])sit[j]=j+a[j],cnt[j]=1;
else sit[j]=sit[j+a[j]],cnt[j]=cnt[j+a[j]]+1;
}
}
int solve(int k){
int ans=0;
while(sit[k]<=n){
ans+=cnt[k];
k=sit[k];
}
return ans+cnt[k];
}
void updata(int x,int k){
a[x]=k;int i=pos[x];
for(int j=R[i];j>=L[i];--j){
if(j+a[j]>R[i])sit[j]=j+a[j],cnt[j]=1;
else sit[j]=sit[j+a[j]],cnt[j]=cnt[j+a[j]]+1;
}
}
int main(){
ios::sync_with_stdio(false);
init();cin>>m;while(m--){
int opt,x,k;cin>>opt>>x;x++;
if(opt==1)cout<<solve(x)<<"\n";
else {cin>>k;updata(x,k);}
}
return 0;
}
排队
首先求出原始序列的逆序对数\(cnt\),然后我们来思考一个简化版问题:
删除一个数会对逆序对数产生什么影响?
设\(a_i\)表示第\(i\)个数的值,\(f(i)=\sum_{k=1}^i[a_k>a_i],g(i)=\sum_{k=i}^n[a_k<a_i]\),则删去它会使得\(cnt'=cnt-f(i)-g(i)\)
同理,在这个位置插入数\(a_i\),会使得\(cnt'=cnt+f(i)+g(i)\)
考虑求出\(f,g\),显然可以使用动态规划配合数据结构做到\(O(n\log n)\)(平衡树/权值线段树边递推边插入)。带上维护就是个树套树(\(O(n\log^2 n)\))就行。
食用复杂度较劣的分块(但跑得飞快)。
算上交换两个数\(a_x,a_y(x<y)\),实质上有影响的只是\([x,y]\),我们仅仅需要统计\([x,y]\)中有多少个数大于/小于\(a_x\),有多少个数大于/小于\(a_y\)即可。
考虑进行分块,复制一遍,暴力排序,然后对于统计,在散块暴力查询,块内二分查找,然后再重构\(pos[x],pos[y]\)两个块就行。
设块长为\(T\),则时间复杂度为:\(O\left(N\log T+TM\log T+M\frac{N}{T}\log T\right)\),乱取\(T=\sqrt{N}\),时间复杂度\(O(M\sqrt{N}\log \sqrt{N})\)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 50500
int pos[N],L[N],R[N],n,m,c[N],a[N],b[N],block,siz,ans,d[N],h[N];
#define lowbit(x) x&-x
void add(int x,int k){
while(x<=n)c[x]+=k,x+=lowbit(x);
}
int ask(int x){
int ans=0;
while(x)ans+=c[x],x-=lowbit(x);
return ans;
}
void init(){
cin>>n;for(int i=1;i<=n;i++)cin>>a[i];
block=sqrt(n),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(n,L[i]+block-1);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
for(int i=1;i<=n;i++)b[i]=a[i],d[i]=a[i];
sort(d+1,d+n+1);int cnt=unique(d+1,d+n+1)-d-1;
for(int i=1;i<=n;i++)
h[i]=lower_bound(d+1,d+cnt+1,a[i])-d;
for(int i=n;i;--i){
add(h[i],1);
ans+=ask(h[i]-1);
}
for(int i=1;i<=siz;i++)sort(b+L[i],b+R[i]+1);
}
void solve(int x,int y){
if(x>y)swap(x,y);
int cnt1=0,cnt2=0,cnt3=0,cnt4=0;
if(pos[x]==pos[y]){
for(int i=x+1;i<y;i++){
if(a[i]>a[x])cnt1++;
if(a[i]<a[y])cnt2++;
if(a[i]<a[x])cnt3++;
if(a[i]>a[y])cnt4++;
}
ans=ans+cnt1+cnt2-cnt3-cnt4;
if(a[x]>a[y])ans--;
if(a[x]<a[y])ans++;//细节
swap(a[x],a[y]);
return ;
}
for(int i=pos[x]+1;i<pos[y];i++){
cnt1+=R[i]-(upper_bound(b+L[i],b+R[i]+1,a[x])-b)+1;
cnt4+=R[i]-(upper_bound(b+L[i],b+R[i]+1,a[y])-b)+1;
cnt2+=lower_bound(b+L[i],b+R[i]+1,a[y])-b-L[i];
cnt3+=lower_bound(b+L[i],b+R[i]+1,a[x])-b-L[i];
}
for(int i=x+1;i<=R[pos[x]];i++){
if(a[i]>a[x])cnt1++;
if(a[i]<a[y])cnt2++;
if(a[i]<a[x])cnt3++;
if(a[i]>a[y])cnt4++;
}
for(int i=L[pos[y]];i<y;i++){
if(a[i]>a[x])cnt1++;
if(a[i]<a[y])cnt2++;
if(a[i]<a[x])cnt3++;
if(a[i]>a[y])cnt4++;
}
ans=ans+cnt1+cnt2-cnt3-cnt4;
if(a[x]>a[y])ans--;
if(a[x]<a[y])ans++;
int s=a[x],t=a[y];swap(a[x],a[y]);
for(int i=L[pos[x]];i<=R[pos[x]];i++)if(b[i]==s){b[i]=t;break;}
for(int i=L[pos[y]];i<=R[pos[y]];i++)if(b[i]==t){b[i]=s;break;}
sort(b+L[pos[x]],b+R[pos[x]]+1);
sort(b+L[pos[y]],b+R[pos[y]]+1);
}
int main(){
ios::sync_with_stdio(false);
init();cout<<ans<<"\n";
cin>>m;while(m--){
int x,y;cin>>x>>y;
solve(x,y);cout<<ans<<"\n";
}
}
弑破抹净的分块变形
基础思想
莫队算法的思想大概是这样的,对询问进行分块,必须离线操作,充分利用历史上的答案
基于分块思想,且\([l,r]\)的答案向\([l,r+1],[l,r-1],[l-1,r],[l+1,r]\)四个相邻状态任意一个转移都是\(O(1)\)的
离线思想,将读入排序,按\(\sqrt{n}\)分块,每\(\sqrt{n}\)个为一块
排序时,将左端点块号相同的询问放在一个块里,右端点按单增排
对于每个块内相邻的两个询问,每次左右端点移动不会超过\(\sqrt{n}\),是\(O(\sqrt{n})\)
块与块间相邻的两个询问,每次左右端点移动不会超过\(2\sqrt{n}\),也是\(O(\sqrt{n})\)
试想以长度x为一块,\([1,x][x+1,2x]\),最坏就是\([1,1]->[2x,2x]\)
因此,对于\(m\)个询问,复杂度为\(O(m\sqrt{n})\)
本来可以通过将\([l,r]\)转化为平面坐标\((l,r)\),通过求曼哈顿最小生成树使得转移和最小,
但是,最坏情况下,曼哈顿最小生成树的复杂度和莫队分块的复杂度是一样的,
相比之下,莫队还好写,所以往往采用莫队算法来写
实现时,分块和下标移动套板子,魔改add、del函数即可
对于排序询问这个有一个小优化,如果l所在块的编号为奇数则按r升序排序,偶数则按r降序排序。
模板
//排序
inline bool cmp(query a,query b){
return a.bl!=b.bl?a.l<b.l:((a.bl&1)?a.r<b.r:a.r>b.r);
}
//处理问题
l=ask[1].l,r=ask[1].r;
……//暴力计算答案
for(int i=2;i<=m;i++){
while (l<ask[i].l) del(c[l++]);
while (l>ask[i].l) add(c[--l]);
while (r<ask[i].r) add(c[++r]);
while (r>ask[i].r) del(c[r--]);//将答案移动至指定范围
ans[ask[i].id]=……;
}
大概流程是这样的:
算法大概遵循一个这样的流程:
- 对于所有区间端点的移动,我们要设计出一种\(O(1)\)的方法使得我们可以快速维护移动端点后一个区间的答案。
- 有了这种方法之后,我们根据刚才的复杂度分析,我们对整个序列分块,每一块大小 \(O(\sqrt{n})\)
- 然后我们对所有询问的区间排序,排序完之后左端点每一次最多移动 \(\sqrt{n}\) 的距离总共 \(n\) 次,右端点单调不降所以每一个块移动 \(n\) 的距离总共 \(\sqrt{n}\) 次,所以总复杂度为 \(O(n\sqrt{n})\)
下面一个很简单的莫队应用,给定\(m\)次询问,每次询问\([l,r]\)中数\(x\)的出现次数
int block,ans[100005],siz,pos[100005],a[10005],cnt[100005],n,m;
struct node{
int l,r,x,id;
}ask[100050];
void add(int x){
cnt[x]++;
}
void del(int x){
cnt[x]--;
}
bool cmp(node a,node b){
return pos[a.l]==pos[b.l]?(pos[a.l]&1?a.r<b.r:a.r>b.r):pos[a.l]<pos[a.r];
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
block=sqrt(n),siz=n%block?n/block+1:block;
for(int i=1;i<=siz;i++){
int l=(i-1)*block+1,r=min(n,block*i);
for(int j=l;j<=r;j++)pos[j]=i;
}
for(int i=1;i<=m;i++){
scanf("%d%d%d",ask[i].l,ask[i].r,ask[i].x);
ask[i].id=i;
}
sort(ask+1,ask+m+1,cmp);
int l=ask[1].l,r=ask[1].r;
for(int i=l;i<=r;i++)add(a[i]);
ans[ask[1].id]=cnt[ask[i].x];
for(int i=2;i<=m;i++){
while(l>ask[i].l)add(a[--l]);
while(l<aks[i].l)del(a[l++]);
while(r<ask[i].r)add(a[++r]);
while(r>ask[i].r)del(a[r--]);
ans[ask[i].id]=cnt[ask[i].x];
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
}
当然这道题也可以用上文所述的朴素分块的\(O(n\sqrt{n})\)或者\(vector\)解法(更加优秀)
莫队算法的应用与变形
普通莫队应用举例
XOR and Favorite Number
- 给定一个长度为\(n\)的序列\(a\),然后再给一个数字\(k\),再给出\(m\)组询问,每组询问给出一个区间,求这个区间里面有多少个子区间的异或值为\(k\)。
-\(1 \le n,m \le 10 ^ 5\),\(0 \le k,a_i \le 10^6\),\(1 \le l_i \le r_i \le n\)。
分析
看到异或区间和,条件反射式想到异或前缀和,那么我们首先构造原序列的异或前缀和\(s\)。看本题,不难发现是个莫队,考虑如何快速实现增删一个端点
假设当前的需要增删的是区间端点是\(x\),那么就是求当前莫队的区间\([l,r]\)内有多少个数\(y\)满足x^y=k,可以推出y=k^x,此题就变成了一道莫队的查询某个值出现的次数,由于值域在\(10^6\)范围,所以可以开一个桶维护。
需要注意的是,异或前缀和查询区间异或和是需要左端点减一的,解决方案可以让所有的区间的左端点向左移动一位。
还有一些细节:在增加一个数进入区间的时候得先统计再插入,在删除的时候要先统计再删除
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
#define N 100050
struct node {
int l, r, id;
}ask[N];
int n, m, block, ans[N], cnt[25*N], s[N], sum, k;
inline int get(int x) {
return (x-1) / block+1;
}
bool cmp(node a, node b) {
return get(a.l) == get(b.l) ? (get(a.l) & 1 ? a.r<b.r : a.r>b.r) : a.l < b.l;
}
void init() {
cin >> n >> m >> k;
block = sqrt(n);
for (int i = 1; i <= n; i++) {
cin >> s[i];
s[i] ^= s[i - 1];
}
for (int i = 1; i <= m; i++) {
cin >> ask[i].l >> ask[i].r;
ask[i].id = i, ask[i].l--;
}
sort(ask + 1, ask + m + 1, cmp);
}
void add(int x) {
sum += cnt[s[x] ^ k];
cnt[s[x]]++;
}
void del(int x) {
cnt[s[x]]--;
sum -= cnt[s[x] ^ k];
}
signed main() {
ios::sync_with_stdio(false);
init();
int l = 1, r = 0;
for (int i = 1; i <= m; i++) {
while (l > ask[i].l)add(--l);
while (r < ask[i].r)add(++r);
while (l < ask[i].l)del(l++);
while (r > ask[i].r)del(r--);
ans[ask[i].id] = sum;
}
for (int i = 1; i <= m; i++) {
cout << ans[i] << endl;
}
}
带修莫队
没想到吧,这玩意还能带修,但只能单点修改
带修莫队的原理是:给每一个询问加一个时间戳\(t\),表示在这个询问之前进行了\(t\)次修改,一个很暴力的思路是:
- 首先设计出此题若不考虑修改,普通莫队怎么做
- 对每一个查询打上时间戳\(t\)
- 正常莫队,在每一次莫队的调整\(l,r\)后,调整\(t\)这一维度,对于修改的位置直接暴力修改
- 需要注意,修改的值与原序列的值要交换,因为\(t\)可能会滚回来,改回来
需要注意的是,我们将\(t\)作为第三维度,对于右端点在同一个块内的按照\(t\)升序排序
光说不练假把式,上模版
void change(int l,int r,int t){//表示当前询问区间是l,r,需要进行第$t$次更改
int id=b[t].x;//更改位置
if(l<=id&&id<=r){
del(s[id]);
add(b[t].y);
}
swap(s[id],b[t].y);//必须交换,有可能这个位置会改回来
}
int get(int x){return (x-1)/block+1;}
bool cmp(node a,node b){
return get(a.l)==get(b.l)?(get(a.r)==get(b.r)?a.t<b.t:a.r<b.r):a.l<b.l;
}
//main函数中
for(int i=1;i<=n;i++)cin>>s[i];//原序列
for(int i=1;i<=m;i++){
int opt,l,r;
cin>>opt>>l>>r;
if(opt==1)b[++lst]={l,r};//修改操作,对位置为l的数进行r的修改
else a[++tot]={l,r,lst,tot};//查询操作
}
sort(a+1,a+tot+1,cmp);//排序
int l=1,r=0,t=0;
for(int i=1;i<=tot;i++){
while(l<a[i].l)del(s[l++]);
while(l>a[i].l)add(s[--l]);
while(r>a[i].r)del(s[r--]);
while(r<a[i].r)add(s[++r]);
while(t<a[i].t)change(l,r,++t);
while(t>a[i].t)change(l,r,t--);
ans[a[i].id]=sum;
}
来分析分析复杂度:
设块长为\(b\),我们有\(\frac{n^2}{b^2}\)个左端点的块的编号一致,右端点的块的编号一致组成的数对,又因为对于这样的数对中\(t\)是单调递增的,所以最多滚\(n\)次,故这部分算法复杂度是\(O(\frac{n^3}{b^2})\),然后因为左右端点的修改都会跳\(O(b)\)次,一共有\(O(n)\)组左右端点所属块不同的区间,总复杂度即为\(O(\frac{n^3}{b^2}+nb)\),由均值不等式,当\(\frac{n^3}{b^2}=nb\)时,复杂度最小,变式换算得到\(n^2=b^3\),也即\(b=\sqrt[\frac{2}{3}]{n}\)时最小,此时总复杂度为\(O(n^{\frac{5}{3}})\),总比暴力好。实际上由于常数较小的优点,部分\(10^5\)数据是能够跑过的
来两道例题:
P2464
一句话题意:给定一段区间,支持单点修改和区间定值出现数量查询
套路:离线,离散化,开一个计数数组计数,然后就变成了板子。。。
例2
题意:给定一个序列,有两种操作
1 x y表示将位置为x的数改为y
2 l r表示查询区间\([l,r]\)中出现过的一次的数的个数.
提示:值域与\(n\)同级
很明显开个桶记录每个数出现次数,那么对于add,del,change三个函数的设置就很简单了。具体地,
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define N 300500
struct node{
int l,r,t,id;
}a[N];
struct Node {
int x,y;
}b[N];
int block;
int get(int x){
return x/block;
}
int n,m,cnt[N],tot,ans[N],s[N],sum,lst;
bool cmp(node a,node b){
return get(a.l)==get(b.l)?(get(a.r)==get(b.r)?a.t<b.t:a.r<b.r):a.l<b.l;
}
void add(int x){
if(cnt[x]==0)sum++;
if(cnt[x]==1)sum--;
cnt[x]++;
}
void del(int x){
if(cnt[x]==1)sum--;
if(cnt[x]==2)sum++;
cnt[x]--;
}
void change(int l,int r,int t){
int id=b[t].x;
if(l<=id&&id<=r){
del(s[id]);
add(b[t].y);
}
swap(s[id],b[t].y);
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
memset(ans,-1,sizeof ans);
block=pow(n,0.67);
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=m;i++){
int opt,l,r;
cin>>opt>>l>>r;
if(opt==1)b[++lst]={l+1,r};
else a[++tot]={l+1,r+1,lst,tot};
}
sort(a+1,a+tot+1,cmp);
int l=1,r=0,t=0;
for(int i=1;i<=tot;i++){
while(l<a[i].l)del(s[l++]);
while(l>a[i].l)add(s[--l]);
while(r>a[i].r)del(s[r--]);
while(r<a[i].r)add(s[++r]);
while(t<a[i].t)change(l,r,++t);
while(t>a[i].t)change(l,r,t--);
ans[a[i].id]=sum;
}
for(int i=1;i<=tot;i++)cout<<ans[i]<<"\n";
return 0;
}
Machine Learning
感觉一般数据结构根本无法维护,考虑莫队。
先分析如果没有修改怎么办,即add与del如何设计
很有用的性质:每个数add与del的时候,最多使得这个数出现次数改变\(1\),考虑这个1如何维护。因为它维护的是区间出现次数,不妨考虑先离散化,再开桶来维护每个数出现的次数,记为\(cnt1\),再开一个桶维护每个出现次数一共有几个,记为\(cnt2\),这样我们可以保证\(O(1)\)统计出来次数,考虑如何求解mex
设当前统计出的mex为\(sum\),首先答案不可能为0,当我们需要更改\(sum\)的时候,也仅仅会改变两个值,记为\(x,y\),先来讨论add
假设我们加入了数\(s\),那么就需要
cnt2[cnt1[s]]--;//此时为0可能会更新mex
cnt1[s]++;
cnt2[cnt1[s]]++;
考虑其对mex的影响,当第一次减去\(cnt2\)时,若其为0则可能会更新\(mex\),取\(\min\)即可,问题在于若原本\(mex\)为后面增加的那个\(cnt2\)
考虑如何维护这个更改,此时肯定是往后找到第一个为0的\(cnt2\),但好似这个过程没有什么可以优化的,还不如区间移动到好了直接暴力mex
但直接暴力求解mex复杂度如何呢,让我们想想,从1开始扫,最坏情况下,即为有一个数出现1次,一个数出现2次,一个数出现3次……一直到\(x\),那么,可以发现,总得数的数量为:\(\sum_{i=1}^xi\le n\),所以说这个暴力求解的复杂度是远小于单次\(O(\sqrt n)\)的,故总的复杂度也就\(O(n\sqrt n)\),那么莫队的复杂度大于它,故不会影响复杂度
于是我们就得到了一个看似无比暴力的莫队算法,add,del完全只需要维护cnt1,cnt2即可,无需考虑影响,最后当\(l,r,t\)三维归一,则暴力扫描mex即可。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define N 500050
int a[N],b[N],c[N],ans[N],cnt1[N],cnt2[N],num,n,m,lst,tot,block;
struct node{
int l,r,t,id;
}ask[N];
struct Node{
int x,y;
}upd[N];
inline int get(int x){
return (x-1)/block+1;
}
bool cmp(node a,node b){
return get(a.l)==get(b.l)?(get(a.r)==get(b.r)?a.t<b.t:a.r<b.r):a.l<b.l;
}
void add(int x){
cnt2[cnt1[x]]--;
cnt1[x]++;
cnt2[cnt1[x]]++;
}
void del(int x){
cnt2[cnt1[x]]--;
cnt1[x]--;
cnt2[cnt1[x]]++;
}
void change(int l,int r,int t){
int id=upd[t].x;
if(l<=id&&id<=r){
del(a[id]);
add(upd[t].y);
}
swap(upd[t].y,a[id]);
}
int find(){
for(int i=1;i;i++){
if(!cnt2[i])return i;
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m;
num=n;
block=pow(n,0.67);
for(int i=1;i<=n;i++){
cin>>a[i];
c[i]=a[i];
}
for(int i=1;i<=m;i++){
int opt,l,r;
cin>>opt>>l>>r;
if(opt==1)ask[++tot]={l,r,lst,tot};
else upd[++lst]={l,r},c[++num]=r;
}
sort(c+1,c+num+1);
num=unique(c+1,c+num+1)-c-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(c+1,c+num+1,a[i])-c;
for(int i=1;i<=lst;i++)upd[i].y=lower_bound(c+1,c+num+1,upd[i].y)-c;
sort(ask+1,ask+tot+1,cmp);
for(int i=1,l=1,r=0,t=0;i<=tot;i++){
while(l<ask[i].l)del(a[l++]);
while(l>ask[i].l)add(a[--l]);
while(r<ask[i].r)add(a[++r]);
while(r>ask[i].r)del(a[r--]);
while(t<ask[i].t)change(l,r,++t);
while(t>ask[i].t)change(l,r,t--);
ans[ask[i].id]=find();
}
for(int i=1;i<=tot;i++)printf("%d\n",ans[i]);
}
回滚莫队
由于莫队的核心操作是\(add,del\)两个,整个莫队的复杂度基于这两个函数的算法复杂度乘上\(O(N\sqrt N)\).
但很多时候,莫队算法的这两个函数其中一个仍然可以保证\(O(1)\),但另一个函数的复杂度较高,比如\(\log n,\sqrt n\)之类的,此时普通的莫队算法就不能解决问题。
我们就有了回滚莫队的算法,对于\(add,del\)哪一个复杂度较高,又可以划分为两类:只删不增的回滚莫队,只增不删的回滚莫队,其核心思想是通过不断记录标记,将指针拉回,化增加/删除为撤销(即不改变答案,只\(O(1)\)更改维护的信息)。
只删不增的回滚莫队
这里主要是先暴力统计大区间答案,再通过不断删这个大区间达到只删不增的效果
- 首先将询问的区间以左端点所在块为第一关键字升序,以右端点为第二关键字降序排序
- 对于左右端点都在同一个块的询问,直接暴力统计答案,复杂度为\(O(\sqrt N)\)
- 对于左端点在同一个块的询问,将\(l\)初始化为这个块的左端点,将\(r\)初始化为\(n\),这部分先暴力统计这段答案,复杂度一般\(O(N)\)
- 由于右端点降序,在处理这同一个块的询问的时候,右端点单调递减,只用删除
- 由于左端点可能无序,考虑建立\(tmp\)先记录下左端点为块的左端点的答案,然后将左端点向右移动,同样是只用删除,当到达指定位置之后,统计一次答案,然后撤销删除,但不统计答案,当撤销回块左端点时,再将答案重新变为\(tmp\)
在实现上,为了代码的方便,可以给左右端点在同一个块的区间单独开一组统计数组来暴力求解
//只删不增回滚莫队伪代码
void del(int x) {
}
void move(int x) {
//删除的逆操作,但不更新答案
}
void solve() {//pos表示所属块
int lst = 0,l=1,r=0;//上个询问所属哪一个块
for (int i = 1; i <= tot; i++) {
if (pos[a[i].l] == pos[a[i].r]) {
//暴力处理块内的询问
ans[a[i].id]=//
//撤销暴力统计的操作
continue;
}
if (lst != pos[a[i].l]) {
lst = pos[a[i].l];//需要再次初始化一次
while (l < L[lst])del(l++);
while (r < n)move(++r);
//暴力计算此时答案
}
while (r > a[i].r)del(r--);
int tmp =/*此时答案*/;
while (l < a[i].l)del(l++);
ans[a[i].id]= ;
while (l > L[pos[a[i].l]])move(--l);
/*此时答案*/ = tmp;
}
}
不难得知,复杂度为\(O(N\sqrt N)\)
Rmq Problem / mex
首先按照套路维护计数数组,然后考虑删除怎么做,很明显,令这个数出现次数减一,减到0就更新答案,那么剩下的都只是套一下即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 500050
#define re register
int n, m, cnt[N], cnt1[N], sum, pos[N], L[N], R[N], s[N], ans[N], block, siz;
struct node {
int l, r, id;
bool operator<(const node& b)const {
return pos[l] == pos[b.l] ? r > b.r : l < b.l;
}
}a[N];
inline void init() {
cin >> n >> m;
block = sqrt(n), siz = n / block + (n % block != 0);
for (re int i = 1; i <= siz; i++)L[i] = R[i - 1] + 1, R[i] = R[i - 1] + block;
R[siz] = n;
for (re int i = 1; i <= siz; i++) {
for (re int j = L[i]; j <= R[i]; j++) {
pos[j] = i;
}
}
for (re int i = 1; i <= n; i++)cin >> s[i];
for (re int i = 1; i <= m; i++) {
cin >> a[i].l >> a[i].r;
a[i].id = i;
}
sort(a + 1, a + m + 1);
return;
}
inline void del(int x) {
cnt[s[x]]--;
if (cnt[s[x]] == 0)sum = min(sum, s[x]);
return;
}
inline void move(int x) {
cnt[s[x]]++;
return;
}
inline void solve() {
int lst = 0, l = 1, r = 0;
for (re int i = 1; i <= m; i++) {
if (pos[a[i].l] == pos[a[i].r]) {
for (re int j = a[i].l; j <= a[i].r; j++) {
cnt1[s[j]]++;
}
for (re int k = 0; k <= a[i].r - a[i].l + 1; k++) {
if (cnt1[k] == 0) {
ans[a[i].id] = k;
break;
}
}
for (re int j = a[i].l; j <= a[i].r; j++) {
cnt1[s[j]]--;
}
continue;
}
if (lst != pos[a[i].l]) {
lst = pos[a[i].l];
while (l < L[lst])del(l++);
while (r < n)move(++r);
for (re int i = 0; i <= n; i++) {
if (!cnt[i]) {
sum = i; break;
}
}
}
while (r > a[i].r)del(r--);
int tmp = sum;
while (l < a[i].l)del(l++);
ans[a[i].id] = sum;
while (l > L[lst])move(--l);
sum = tmp;
}
return;
}
int main() {
// freopen("P4137_4.in","r",stdin);
// freopen("P4137_4.ans","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
init();
solve();
for (re int i = 1; i <= m; i++)cout << ans[i] << "\n";
return 0;
}
只增不删的回滚莫队
类比只删不增的回滚莫队,容易想到可以这样做:
- 将询问区间按左端点所在块为第一关键字递增排序,右端点为第二关键字递增排序
- 对于每个块,初始化\(l=R[i]+1,r=l-1\),这是一个空区间
- 对于左右端点在同一个块内的询问,暴力处理即可
- 否则,对于右端点的处理,由于递增,所以只增不删
- 对于左端点,先记录下此时的答案,然后只增不删往左滚,更新答案之后原路撤销操作
- 将答案还原即可
这里没有处理新开的块,原因是本身是一个空区间
板子大概类似
void add(int x) {
}
void move(int x) {
}
void solve() {
int lst = 0, l = 1, r = 0;
for (int i = 1; i <= tot; i++) {
if (pos[a[i].l] == pos[a[i].r]) {
//用那个另开的统计数组暴力统计答案
and[a[i].id]=
//撤销掉所有操作
continue;
}
if (lst != pos[a[i].l]) {
while (l <= R[pos[a[i].l]])move(l++);
while (r > R[pos[a[i].l]])move(r--);
//重置答案
lst = pos[a[i].l];
}
while (r < a[i].r)add(++r);
int tmp =/*此时答案*/;
while (l > a[i].l)add(--l);
ans[a[i].id] =/*此时答案*/;
/*此时答案*/ = tmp;
while (l <= R[pos[a[i].l]])move(l++);
}
}
例题:洛谷模版
给定一个序列,多次询问一段区间 \([l,r]\),求区间中相同的数的最远间隔距离。
序列中两个元素的间隔距离指的是两个元素下标差的绝对值。
解法1
考虑回滚莫队的常规操作,由于要求相同元素距离最大值,显然必须对于每一个值都求出相邻元素最大值,而欲求这个最大值,就必须知道当前区间每个值最后出现的位置和最先出现的位置,分别记为\(ed,st\).
考虑如何维护这两个值。由于我们每处理完一个块的询问之后会重置,无需考虑不同块的相互影响,那么仅需考虑一个块如何维护即可。
由于回滚莫队的性质,显然\(r\)单调递增,\(ed\)和\(st\)就可以肆无忌惮的在\(r\)中更新,很简单不多说。而至于要回滚的\(l\)指针,则不能维护\(st\),因为无法撤销,但幸好,当前\(l\)指针所在位置,就是这个位置对应值的\(st\).
故我们只需要对只出现于\(l\)移动范围的值更新\(ed\)即可。那么最后回滚的时候,如果发现回滚的\(l\)指针这个位置的\(ed\)指向自己,就重置为0。在每个块询问处理完之后,不要忘记清空两数组
同块暴力很简单,不多说
#include<iostream>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
#define N 5000005
int s[N],n,m,L[N],R[N],pos[N],ans[N],block,siz,sum,st[N],ed[N],st1[N],ed1[N],b[N],c[N],cnt,vis[N];
struct node{
int l,r,id;
bool operator<(const node b ){
return pos[l]==pos[b.l]?r<b.r:l<b.l;
}
}a[N];
void init(){
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
for(int i=1;i<=n;i++)c[i]=s[i];
sort(c+1,c+n+1);
cnt=unique(c+1,c+n+1)-c-1;
for(int i=1;i<=n;i++){
s[i]=lower_bound(c+1,c+cnt+1,s[i])-c;
// cout<<s[i]<<" ";
}
//cout<<endl;
cin>>m;
for(int i=1;i<=m;i++){
int l,r;
cin>>l>>r;
a[i]={l,r,i};
}
block=sqrt(n);
siz=n/block+(n%block!=0);
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=R[i-1]+block;
R[siz]=n;
for(int i=1;i<=siz;i++){
for(int j=L[i];j<=R[i];j++){
pos[j]=i;
}
}
sort(a+1,a+m+1);
}
void addr(int x){
ed[s[x]]=x;
if(!st[s[x]])st[s[x]]=x;
sum=max(sum,ed[s[x]]-st[s[x]]);
}
void addl(int x){
if(!ed[s[x]])ed[s[x]]=x;
sum=max(ed[s[x]]-x,sum);
}
void movel(int x){
if(ed[s[x]]==x)ed[s[x]]=0;
}
void solve(){
int l=1,r=0,lst=0;
for(int i=1;i<=m;i++){
if(pos[a[i].l]==pos[a[i].r]){
int sum=0;
for(int j=a[i].l;j<=a[i].r;j++){
if(!st1[s[j]])st1[s[j]]=j;
sum=max(sum,j-st1[s[j]]);
}
ans[a[i].id]=sum;
for(int j=a[i].l;j<=a[i].r;j++){
st1[s[j]]=0;
}
continue;
}
if(lst!=pos[a[i].l]){
lst=pos[a[i].l];
for(int i=l;i<=r;i++)ed[s[i]]=st[s[i]]=0;
l=R[lst]+1,r=R[lst];
sum=0;
}
while(r<a[i].r)addr(++r);
int tmp=sum;
while(l>a[i].l)addl(--l);
ans[a[i].id]=sum;
while(l<=R[lst])movel(l++);
sum=tmp;
}
}
int main(){
ios::sync_with_stdio(false);
init();
solve();
for(int i=1;i<=m;i++)cout<<ans[i]<<"\n";
return 0;
}
解法2
有一说一,此题不用回滚莫队,可以\(O(n)\)的预处理出每个数出现的位置的前一个和后一个出现位置,那么将\(add,del\)都分\(l,r\)讨论,借助前驱后继即可进行更新
广袤包围的值域分块
值域分块是一种对值域进行分块的算法,是一种支持高速插入(\(O(1)\)),低速查询的数据结构(\(O(\sqrt n)\))
举个例子:仅有\(O(n)\)次查询,却有\(O(n\sqrt n)\)次插入的时候,用线段树/树状数组就会挂掉,食用值域分块可以做到\(O(n\sqrt n)\)
几个考察方向:
- 序列分块套值域分块->lxl毒瘤
- 值域分块+莫队:\(O(\sqrt n)\)统计一次答案,最终复杂度不会变化
下面搞几道例题:
区间第k小问题
传统做法:树套树(两三百行的代码+超难调试,常数极大,勇夫请上!)
“高科技做法”:莫队+值域分块
具体地,我们还是对询问进行离线排序,离散化,将值域分块,然后在移动区间的时候,在适当的块插入一个值(标记为true或者次数++都可以),每个块记录数的总数,最后移动到了位置,统计答案的时候就直接一块一块找,如果次数小于\(k\),\(k-=siz\),继续下一块。否则直接跳到这个块里暴力找。
然后,然后就没了。
带修咋办捏?你怕是忘了带修莫队。
无修精致Code:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
#define N 205000
int a[N],b[N],cnt[N],L[N],R[N],block,siz,pos[N],sum[N],n,m,s,ans[N];
inline int get(int x){return (x+block-1)/block;}
struct node{
int l,r,k,id;
bool operator<(const node b)const {
return get(l)==get(b.l)?r<b.r:l<b.l;
}
}ask[N];
void init(){
cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)b[i]=a[i];sort(b+1,b+n+1);
s=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+s+1,a[i])-b;
block=sqrt(s),siz=(s+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(L[i]+block-1,s);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
for(int i=1;i<=m;i++)cin>>ask[i].l>>ask[i].r>>ask[i].k;
for(int i=1;i<=m;i++)ask[i].id=i;
}
void add(int x){x=a[x];
cnt[x]++,sum[pos[x]]++;
}
void del(int x){x=a[x];
cnt[x]--,sum[pos[x]]--;
}
int find(int k){
for(int i=1;i<=siz;i++){
if(sum[i]<k)k-=sum[i];
else for(int j=L[i];j<=R[i];j++){
if(cnt[j]<k)k-=cnt[j];
else return j;
}
}
return -1;
}
void solve(){
sort(ask+1,ask+m+1);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(l<ask[i].l)del(l++);
while(l>ask[i].l)add(--l);
while(r<ask[i].r)add(++r);
while(r>ask[i].r)del(r--);
ans[ask[i].id]=find(ask[i].k);
}
for(int i=1;i<=m;i++)cout<<b[ans[i]]<<"\n";
}
int main(){
init();solve();
return 0;
}
作业
设原序列为\(a_1\sim a_n\)
将一个询问拆成两个,先看第一个询问:
\(\sum_{k=l}^r[a\le a_k][a_k\le b]=\sum_{k=l}^r[a_k\le b]-\sum_{k=l}^r[a_k\le a-1]\).
拆成前缀和形式之后,在莫队移动区间时直接记录出现次数和位置,然后分块求和即可。
对于第二个询问,cnt表示出现次数,对于每个块中累计的答案,只有cnt[x]=0/1的时候进行更改,也是分块求和即可
所以你A掉了一道紫题板子题
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<set>
#include<cmath>
#include<queue>
#include<deque>
#include<map>
#include<stack>
#include<cstring>
using namespace std;
#define MAXN 105000
const int N=100000;
int L[MAXN],R[MAXN],pos[MAXN],block,siz,cnt[MAXN],sum1[MAXN],sum2[MAXN],n,m,a[MAXN],ans1[MAXN],ans2[MAXN];
struct node{
int l,r,a,b,id;
bool operator<(node b){
return pos[l]==pos[b.l]?r<b.r:l<b.l;
}
}ask[MAXN];
void init(){
block=sqrt(N),siz=(N+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(L[i]+block-1,N);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];++j)pos[j]=i;
cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=m;i++)ask[i].id=i;
for(int i=1;i<=m;i++)cin>>ask[i].l>>ask[i].r>>ask[i].a>>ask[i].b;
}
void add(int x){x=a[x];
if(!cnt[x])sum2[pos[x]]++;
cnt[x]++,sum1[pos[x]]++;
}
void del(int x){x=a[x];
if(cnt[x]==1)sum2[pos[x]]--;
cnt[x]--,sum1[pos[x]]--;
}
int find(int k){
int ans=0;
for(int i=1;i<=siz;i++){
if(R[i]<=k)ans+=sum1[i];
else {for(int j=L[i];j<=k;j++)ans+=cnt[j];break;}
}
return ans;
}
int query(int l,int r){
int ans=0;
if(pos[l]==pos[r]){
for(int i=l;i<=r;i++)ans+=(cnt[i]>=1);
return ans;
}
for(int i=l;i<=R[pos[l]];i++)ans+=(cnt[i]>=1);
for(int i=L[pos[r]];i<=r;i++)ans+=(cnt[i]>=1);
for(int i=pos[l]+1;i<pos[r];i++)ans+=sum2[i];
return ans;
}
void solve(){
int l=1,r=0;sort(ask+1,ask+m+1);
for(int i=1;i<=m;i++){
if(ask[i].a>ask[i].b)continue;
while(l>ask[i].l)add(--l);
while(r<ask[i].r)add(++r);
while(l<ask[i].l)del(l++);
while(r>ask[i].r)del(r--);
ans1[ask[i].id]=find(ask[i].b)-find(ask[i].a-1);
ans2[ask[i].id]=query(ask[i].a,ask[i].b);
}
for(int i=1;i<=m;i++)cout<<ans1[i]<<" "<<ans2[i]<<"\n";
}
int main(){
ios::sync_with_stdio(false);
init();solve();
return 0;
}
神,不惧死亡
一道比较好玩的题。
首先让我们来分析分析,我们显然可以通过一系列操作,将每个数的出现次数化为1/2。对于出现次数为2的数,为了使得最小值最大,显然是选择最小的那个数删掉,然后答案就是那个数的后继。
所以,我们需要维护的是:
区间内出现次数为偶数的最小值的后继
也比较板其实,只是套了个带修而已
食用带修莫队来搞修改操作,修改可以看作删一次加一次。
具体地,我们维护每个块出现次数为偶数的值的个数和出现次数为奇数的值的个数,和每个数的出现次数。
然后在查询中从小到大扫,如果这个块出现过出现次数为偶数的数,就以这个点为起点,向后扫就是。
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define MAXN 105000
int n,m,pos[MAXN],L[MAXN],R[MAXN],sum[MAXN][2],cnt[MAXN],a[MAXN],block,siz,ans[MAXN],c[MAXN];
struct node{
int opt,l,r,p,q,id;
bool operator<(const node b){return pos[l]==pos[b.l]?(pos[r]==pos[b.r]?id<b.id:r<b.r):l<b.l;}
}ask[MAXN],data[MAXN];
void init(){
cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=m;i++){
cin>>ask[i].opt;if(ask[i].opt==1)cin>>ask[i].p>>ask[i].q;
else cin>>ask[i].l>>ask[i].r>>ask[i].p>>ask[i].q;
ask[i].id=i;c[i]=ask[i].opt;data[i]=ask[i];
}
block=pow(n,0.66),siz=(n+block-1)/block;
for(int i=1;i<=siz;i++)L[i]=R[i-1]+1,R[i]=min(L[i]+block-1,n);
for(int i=1;i<=siz;i++)for(int j=L[i];j<=R[i];j++)pos[j]=i;
sort(ask+1,ask+m+1);
}
void add(int x){x=a[x];
cnt[x]++;sum[pos[x]][(cnt[x])&1]++;
if(cnt[x]>1)sum[pos[x]][(cnt[x]&1)^1]--;
}
void del(int x){x=a[x];
cnt[x]--;sum[pos[x]][(cnt[x]&1)^1]--;
if(cnt[x]>0)sum[pos[x]][cnt[x]&1]++;
}
void change(int id,int l,int r){
if(data[id].opt==2)return ;
if(l<=data[id].p&&data[id].p<=r)del(data[id].p);
a[data[id].p]+=data[id].q,data[id].q*=-1;
if(l<=data[id].p&&data[id].p<=r)add(data[id].p);
}
int find(int l,int r){
int ans=-1,tag=0;
if(pos[l]==pos[r]){
for(int i=l;i<=r;i++){
if(tag&&cnt[i])return i;
if((cnt[i]&1)==0&&cnt[i]>0)tag=1;
}
return ans;
}
for(int i=l;i<=R[pos[l]];i++){
if(tag&&cnt[i])return i;
if((cnt[i]&1)==0&&cnt[i]>0)tag=1;
}
for(int i=pos[l]+1;i<pos[r];i++){
if(tag&&sum[i][0]+sum[i][1]>0){
for(int j=L[i];j<=R[i];j++)if(cnt[j])return j;
return ans;
}
if(sum[i][0]&&tag==0){
for(int j=L[i];j<=R[i];j++){
if(tag&&cnt[j])return j;
if((cnt[j]&1)==0&&cnt[j])tag=1;
}
}
}
for(int i=L[pos[r]];i<=r;i++){
if(tag&&cnt[i])return i;
if((cnt[i]&1)==0&&cnt[i]>0)tag=1;
}
return ans;
}
void solve(){
int l=1,r=0,t=0;
for(int i=1;i<=m;i++){
if(ask[i].opt==1)continue;
while(l>ask[i].l)add(--l);
while(r<ask[i].r)add(++r);
while(l<ask[i].l)del(l++);
while(r>ask[i].r)del(r--);
while(t<ask[i].id)change(++t,l,r);
while(t>ask[i].id)change(t--,l,r);
ans[ask[i].id]=find(ask[i].p,ask[i].q);
}
for(int i=1;i<=m;i++){
if(c[i]==1)continue;
cout<<ans[i]<<endl;
}
}
int main(){
ios::sync_with_stdio(false);
init();solve();
}//吉利的88
深遁潜藏的根号分治
思想概述
根号分治,是应对序列问题的方法。对于一个序列问题,设置阀值\(S\),将数分为大于和小于两类,分类处理,达到优化复杂度的目的。\(S\)的大小具体分析。
前置知识:均值不等式
\(\forall a,b\in \mathbb{R^+},\sqrt{ab}\le \frac{a+b}{2}\),当且仅当\(a=b\)取到等号。
证明:\((a-b)^2\ge 0\implies a^2+b^2+2ab\ge 4ab\implies a+b\ge 2\sqrt {ab}\implies \frac{a+b}{2}\ge \sqrt{ab}\)
扩展:
应用举例
哈希冲突
对模数进行根号分治,对\(x<\sqrt n\),\(O(n\sqrt n)\)预处理,\(O(1)\)回答即可
若大于\(\sqrt n\),直接暴力统计,复杂度\(O(\sqrt n)\)
对于修改,重构预处理信息即可。
Swap Swap Sort
首先,考虑目标排列是\(1\sim k\)的初始情况。容易证明:对于一次交换,能且仅能消除一个逆序对,所以最初需要的操作次数就是逆序对个数。
接着考虑将两个数\(x,y\)互换对答案造成的影响。
可以这样等效考虑,在目标情况中对两个数互换,等价于在排序后的序列中将\(x,y\)所在部分交换位置(因为\(x,y\)相邻)。进一步的,我们可以看作\(x'=y,y'=x\),目标序列不变,在原序列中把所有的\(x,y\)交换位置,再求逆序对是一样的。
所以因为\(x,y\)相邻,交换他们的位置只能影响这两个数的相互贡献。设在原序列中,有\(h(x,y)\)个数对\((i,j)\),满足\(i<j,a_i=x,a_j=y\),\(h'(x,y)\)个数对\((i,j)\),满足\(i>j,a_i=x,a_j=y\),则有\(h'(x,y)+h(x,y)=cnt_x\times cnt_y\)。
而交换两数位置,只会有:\(Ans=Ans+h'(x',y')-h(x',y')=Ans+cnt_{x'}\times cnt_{y'}-2h(x',y')\)问题转变为求\(h(x',y')\)。
因为\(h(x',y')\)乍一看不咋好求,考虑根号分治。
设阀值为\(S\),对于\(cnt_x\ge S\),可以\(O(n)\)地预处理出\(x\)与其他所有数之间的答案,这样的数不会超过\(\frac{n}{S}\),故空间复杂度\(O(\frac{n^2}{S})\),时间复杂度\(O(\frac{n^2}{S})\)。
对于一组询问\((x,y)\),\(cnt_x< S,cnt_y<S\),则可以开vector存储每个数出现的位置,双指针扫描一遍,复杂度\(O(qS)\)
总复杂度\(O(\frac{n^2}{S}+qS)\),根据均值不等式,\(\frac{n^2}{S}=qS\)时取得最小值,解得\(S=\frac{n}{\sqrt q}=100\),总复杂度\(O(n\sqrt q)\)。
不过在处理第一种情况的时候,由于空间复杂度为\(O(n\sqrt q)\),吃不消,可以离线下来,单独处理关于每个数的询问,空间复杂度降至\(O(n)\)。
对于目标排列不是\(1\sim k\)的情况,建立一个映射即可转化。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
#define N 100050
#define Q 1000500
#define int long long
struct node{
int x,y,id,tag;
};
vector<node>t[N];
vector<int>seat[N];
int n,m,k,q,s=100,c[N],ans,b[N],a[N],cnt1[N],cnt2[N],c1[N],Ans[Q],f[N],vis[N];
#define lowbit(x) x&-x
void add(int x,int k1){
for(int i=x;i<=k;i+=lowbit(i))c1[i]+=k1;
}
int ask(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i))ans+=c1[i];
return ans;
}
int get(int x,int y){//h(x,y)
int ans=0;
int l=0,r=0,len1=seat[x].size(),len2=seat[y].size();
for(r=0;r<len2;r++){
while(seat[x][l]<seat[y][r]&&l<len1)l++;
ans+=l;
}
return (c[x]*c[y]-2*ans);
}
void init(){
cin>>n>>k>>q;
s=n/sqrt(q)+3;
for(int i=1;i<=k;i++)b[i]=i;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)seat[a[i]].push_back(i);
for(int i=1;i<=n;i++)c[a[i]]++;
for(int i=n;i;--i){
ans+=ask(a[i]-1);
add(a[i],1);
}
for(int i=1;i<=q;i++){
int xb;
cin>>xb;
swap(b[xb],b[xb+1]);
int x=b[xb],y=b[xb+1];
if(c[x]<s&&c[y]<s){
if(c[x]==0||c[y]==0)Ans[i]=0;
else Ans[i]=get(x,y);
}
else {
if(c[x]<s)t[y].push_back((node){y,x,i,-1});
else t[x].push_back((node){x,y,i,1});
}
}
for(int i=1;i<=n;i++){//h(a[i],a[j])
if(c[a[i]]<s||vis[a[i]])continue;
memset(f,0,sizeof f);
int cnt1=0;
for(int j=1;j<=n;j++){
if(a[j]==a[i])cnt1++;
else{
f[a[j]]+=cnt1;
}
}
vis[a[i]]=1;
int len1=t[a[i]].size();
for(int j=0;j<len1;j++){
Ans[t[a[i]][j].id]=t[a[i]][j].tag*(c[t[a[i]][j].x]*c[t[a[i]][j].y]-2*f[t[a[i]][j].y]);
}
}
for(int i=1;i<=q;i++){
ans+=Ans[i];
cout<<ans<<endl;
}
}
signed main(){
// freopen("data.in","r",stdin);
// freopen("data.ans","w",stdout);
ios::sync_with_stdio(false);
init();
}
点缀光辉的数论分块
也叫整除分块
是快速处理含有\(\sum_{i=1}^nf(i)\left\lfloor\frac{n}{i} \right\rfloor\)的式子的方法
性质:
- \(\forall a,b,c\in \mathbb{Z^+},\left\lfloor\frac{a}{bc}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor\)
证明:设\(a=qb+r(0\le r<b)\),\(\frac{a}{bc}=\frac{qb+r}{c}=\frac{qb}{c}+\frac{r}{c}\),而\(q=pc+d(0\le d<c)\),所以
\(\frac{a}{bc}=\frac{\frac{qb+r}{b}}{c}=\frac{q}{c}+\frac{r}{bc}=p+\frac{r+bd}{bc},\left\lfloor\frac{a}{b}\right\rfloor=q,\left\lfloor\frac{q}{c}\right\rfloor=p\)。由于\(d<c\implies bc-bd\ge b\),而\(r<b\),故\(\left\lfloor\frac{a}{bc}\right\rfloor=p=\left\lfloor\frac{q}{c}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{a}{b}\right\rfloor}{c}\right\rfloor\),得证。
- \(S=\lbrace x|\left\lfloor\frac{n}{i}\right\rfloor(0<i\le n)\rbrace\),则\(|S|\le 2\sqrt n\),证明显然
- \(\left\lfloor\frac{n}{x}\right\rfloor=\left\lfloor\frac{n}{l}\right\rfloor>0,x\ge l\)的充要条件是\(x\in[l,\left\lfloor\frac{n}{\left\lfloor\frac{n}{l}\right\rfloor}\right\rfloor]\)
首先,\(g(x)=\frac{n}{x}\)的值在\(x>0\)时是单调递减的,所以满足条件的\(x\)定是块状分布。先来讨论\(l|n\)的情况:
\(l\)显然是这个块的左边界,所以我们实际上是要求出这个块的右边界,设\(kl=n\),则需要求\(\left\lfloor\frac{n}{r}\right\rfloor=k\)的最大的\(r\)
显然,\(\left\lfloor\frac{n}{r}\right\rfloor\le \frac{n}{r}\),所以\(k\le \frac{n}{r}\implies r\le \frac{n}{k}\implies r_{\max}=\left\lfloor\frac{n}{k}\right\rfloor\)。
而若\(l\nmid n\),则显然\(k=\left\lfloor\frac{n}{l}\right\rfloor\)即可。带入原式可知原命题成立
如果是上取整,可以搞成:\(\left\lceil\frac{n}{k}\right\rceil=\left\lfloor\frac{n+k-1}{k}\right\rfloor\),这是显然成立的(分类讨论即可证明)。
平移一个求和下标很容易就可以转化了。
回到之前的问题:求\(\sum_{i=1}^nf(i)\left\lfloor\frac{n}{i} \right\rfloor\),设\(S(i)=\sum_{k=1}^if(k)\),然后直接前缀和搞搞就行。数论分块复杂度\(O(\sqrt n)\)
常见的形式:
ans=n*k;
for(int x=1,gx;x<=n;x=gx+1){
gx=k/x?min(k/(k/x),n):n;
ans-=(k/x)*(x+gx)*(gx-x+1)/2;
}
例题:
清华集训-模积和
默认\(n\le m\)
原式可以写为:
对于式子的前半部分,进行拆开,可以化为:
设\(S=S_1-S_2-S_3+S_4\),分别处理:
\(S_1=\sum_{i=1}^n\sum_{j=1}^mnm=n^2m^2\)
\(S_2=\sum_{i=1}^n\sum_{j=1}^m nj\left\lfloor\frac{m}{j}\right\rfloor=n^2\sum_{j=1}^mj\left\lfloor\frac{m}{j}\right\rfloor\)
\(S_3=m^2\sum_{i=1}^ni\left\lfloor\frac{n}{i}\right\rfloor\)
\(S_4=\sum_{i=1}^ni\left\lfloor\frac{n}{i}\right\rfloor·\sum_{j=1}^m j\left\lfloor\frac{m}{j}\right\rfloor\)
数论分块计算即可。
对于\(S_4\),每次扩展的时候,取块尾较近的扩展即可。
对于式子的后半部分,拆开同样得到:
\(\sum_{i=1}^n(n\bmod i)(m\bmod i)=\sum_{i=1}^n\left(nm-mi\left\lfloor\frac{n}{i}\right\rfloor-ni\left\lfloor\frac{m}{i}\right\rfloor+i^2\left\lfloor\frac{n}{i}\right\rfloor\left\lfloor\frac{m}{i}\right\rfloor\right)\)
同样设其等价于\(S_1-S_2-S_3+S_4\)
则:
\(S_1=n^2m\)
\(S_2=m\sum_{i=1}^n\left\lfloor\frac{n}{i}\right\rfloor\)
\(S_3=n\sum_{i=1}^n\left\lfloor\frac{m}{i}\right\rfloor\)
\(S_4=\sum_{i=1}^n i^2\left\lfloor\frac{n}{i}\right\rfloor\left\lfloor\frac{m}{i}\right\rfloor\)
对于\(S_4\)的处理,也是每次扩展较小的那个块尾。
需要用到一个公式:\(\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}{6}\)
证明:
数学归纳法:当\(n=1\)时,显然成立。设\(n=k\)成立,现在需要证明\(n=k+1\)成立,则需证明:\(6(k+1)^2=(k+1)(k+2)(2k+3)-k(k+1)(2k+1)\),化简后显然成立。
讲真这玩意最多蓝,咋就紫了
关于数论分块的更多知识——>运用在莫反里。
终将到来的块状链表
Ynoi杂题题解
未来日记
题意:支持区间定值修改和区间第\(k\)大,数据范围\(10^5\),空间限制\(512MB\),时间限制\(1000ms\)
显然1e5是分块,考虑怎么做
区间定值修改,做过这个的人都知道使用冰茶姬和桶来支持
但显然,这题桶无法满足我们的需求,求第\(k\)大通用三个方法:可持久化线段树,树套树,值域分块优化莫队
这里前两个一看就是废物,值域分块貌似有优化的空间?
那么考虑使用值域分块来优化,一看lxl开的\(512MB\),\(100\)%是对每个块开一个值域进行维护。
所以说,这时候就涉及到怎么搞的问题了
首先对于区间定值修改,整块直接把\(x\)位置删掉(冰茶姬维护siz,把其有的数插入到\(y\)的位置,并将冰茶姬连上
对于散块先暴力重构然后修改(冰茶姬归零)
再次对于区间第\(k\)大查询,怎么搞呢?
值域分块使得我们只需要快速地知道某个数出现次数就可以找\(k\)大了
总的做法:
按照套路:设\(sum[i][j]\)表示前\(i\)个序列块中前\(j\)个值域块里出现的次数总数,\(cnt[i][j]\)表示前\(i\)个序列块中数\(j\)出现次数总数
显然可以递推求解,复制前一个复杂度\(O(n)\),总共\(O(\sqrt n)\)次。递推总计复杂度\(O(n)\),所以总预处理复杂度\(O(n\sqrt n)\)
再考虑询问:对于这个块,可以先将散块开个桶统计,复杂度\(O(\sqrt n)\),然后直接在整块两端进行差分统计,按照值域分块,一块一块地跳,找到块之后一个个找即可。
最后考虑修改怎么搞:我们以块内此数字第一次出现的位置的下标为代表元
设\(sit[i][j]\)表示第\(i\)个块第一个值为\(j\)的数的下标,\(id[i][j]\)表示第\(i\)个块代表元\(j\)所代表的的值(与\(f\)构成一对映射),设\(f[i]\)表示冰茶姬
则\(a[x]=id[pos[x]][f[x]]\),其中\(pos[x]\)表示\(x\)所属块编号
散块直接按照这个式子还原原序列然后暴力修改重构,并重新统计\(cnt,sum\),由于只涉及两个值,所以复杂度\(O(\sqrt n)\)
对于整块,设当前第\(i\)个块:
-
区间没有\(x\):跳过
-
区间有\(x\)没\(y\),则\(sit[i][y]=sit[i][x],id[i][sit[i][x]]=y,sit[i][x]=0\)
-
有\(x\)还有\(y\),非常麻烦,看上去只能暴力重构,事实上这是正确的。Why?
容易发现,每一个块进行某次操作,出现这种情况,会使得其维护值的个数少一。有操作2的存在,我们可以发现,维护值的个数是单调不增的,所以操作三实际上每个块只会执行\(O(\sqrt n)\)次,总复杂度\(O( n)\),每个块的复杂度总和是\(O(n\sqrt n)\)级的。
这里我们忽视了一个问题:\(cnt,sum\)的更新问题
事实上,在块的后移的时候用变量tmp维护即可。没故意卡常,luogu会T一个点,CQBZOJ可以过
#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
#define N 105500
#define re register
#define S 355
int V=100000;
inline void read(int &x){
x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
}
int n,m,siz,a[N],tot,tt[N],L[S],R[S],pos_v[N],cnt1[S],cnt2[N],cnt[S][N],scnt[S][N],sum[S][S],f[N],sit[S][N],block,len_v=335;
inline int find(int x){
return x==f[x]?x:f[x]=find(f[x]);
}
inline int get(int x){
return (x+block-1)/block;
}
inline void build(int id,int l,int r,int x,int y){
re int tmp=0;
tot=0;
sit[id][x]=sit[id][y]=0;
for(re int i=L[id];i<=R[id];i++){
a[i]=a[find(i)];
if(a[i]==x||a[i]==y)tt[++tot]=i;
}
for(re int i=l;i<=r;i++)if(a[i]==x)a[i]=y,tmp++;
cnt[id][x]-=tmp,cnt[id][y]+=tmp;
for(re int i=1;i<=tot;i++)f[tt[i]]=tt[i];
for(re int i=1;i<=tot;i++){
if(!sit[id][a[tt[i]]])sit[id][a[tt[i]]]=tt[i];
else f[tt[i]]=sit[id][a[tt[i]]];
}
for(int i=id;i<=siz;i++){
scnt[i][x]-=tmp,scnt[i][y]+=tmp;
if(pos_v[x]!=pos_v[y])sum[i][pos_v[x]]-=tmp,sum[i][pos_v[y]]+=tmp;
}
}
inline void change(int l,int r,int x,int y){
re int lpos=get(l),rpos=get(r);
if(lpos==rpos)build(lpos,l,r,x,y);
else {
build(lpos,l,R[lpos],x,y);
build(rpos,L[rpos],r,x,y);
int tmp=0;
for(re int i=lpos+1;i<rpos;i++){
if(sit[i][x]){
if(!sit[i][y])sit[i][y]=sit[i][x],a[sit[i][x]]=y;
else f[sit[i][x]]=sit[i][y];
sit[i][x]=0,tmp+=cnt[i][x],cnt[i][y]+=cnt[i][x],cnt[i][x]=0;
}
scnt[i][x]-=tmp,scnt[i][y]+=tmp;
if(pos_v[x]!=pos_v[y])sum[i][pos_v[x]]-=tmp,sum[i][pos_v[y]]+=tmp;
}
for(re int i=rpos;i<=siz;i++){
scnt[i][x]-=tmp,scnt[i][y]+=tmp;
if(pos_v[x]!=pos_v[y])sum[i][pos_v[x]]-=tmp,sum[i][pos_v[y]]+=tmp;
}
}
}
inline int query(int l,int r,int k){
re int lpos=get(l),rpos=get(r),cnt=0;
if(lpos==rpos){
for(re int i=l;i<=r;i++)a[i]=a[find(i)],cnt1[pos_v[a[i]]]++,cnt2[a[i]]++;
for(re int i=1;i<=len_v;i++){
cnt+=cnt1[i];
if(cnt>=k){
cnt-=cnt1[i];
for(re int j=(i-1)*len_v+1;j<=i*len_v;j++){
cnt+=cnt2[j];
if(cnt>=k){
for(re int i=l;i<=r;i++)cnt2[a[i]]--,cnt1[pos_v[a[i]]]--;
return j;
}
}
}
}
}
else {
for(re int i=l;i<=R[lpos];i++)a[i]=a[find(i)],cnt1[pos_v[a[i]]]++,cnt2[a[i]]++;
for(re int i=L[rpos];i<=r;i++)a[i]=a[find(i)],cnt1[pos_v[a[i]]]++,cnt2[a[i]]++;
for(re int i=1;i<=len_v;i++){
cnt+=cnt1[i]+sum[rpos-1][i]-sum[lpos][i];
if(cnt>=k){
cnt-=cnt1[i]+sum[rpos-1][i]-sum[lpos][i];
for(re int j=(i-1)*len_v+1;j<=i*len_v;j++){
cnt+=cnt2[j]+scnt[rpos-1][j]-scnt[lpos][j];
if(cnt>=k){
for(re int i=l;i<=R[lpos];i++)cnt1[pos_v[a[i]]]--,cnt2[a[i]]--;
for(re int i=L[rpos];i<=r;i++)cnt1[pos_v[a[i]]]--,cnt2[a[i]]--;
return j;
}
}
}
}
}
}
int main() {
read(n);read(m);
for(re int i=1;i<=n;i++){
read(a[i]);f[i]=i;
}
block=sqrt(n),siz=(n+block-1)/block;
for(re int i=1;i<=V;i++)pos_v[i]=(i-1)/len_v+1;
for(re int i=1;i<=siz;i++){
L[i]=R[i-1]+1,R[i]=min(L[i]+block-1,n);
for(re int j=L[i];j<=R[i];j++){
if(!sit[i][a[j]])sit[i][a[j]]=j;
else f[j]=sit[i][a[j]];
cnt[i][a[j]]++;
}
}
for(re int i=1;i<=siz;i++){
for(re int j=1;j<=len_v;j++)sum[i][j]=sum[i-1][j];
for(re int j=L[i];j<=R[i];j++)sum[i][pos_v[a[j]]]++;
for(re int j=1;j<=V;j++)scnt[i][j]=scnt[i-1][j]+cnt[i][j];
}
while(m--){
re int opt,x,y,l,r,k;
read(opt);
if(opt==1){
read(l),read(r),read(x),read(y);
if(x==y)continue;//114514
change(l,r,x,y);
}
else {
read(l),read(r),read(k);
printf("%d\n",query(l,r,k));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号