矩形有交问题—CDQ
矩阵覆盖问题-CDQ分治
[COCI2018-2019#2] Sunčanje
题目描述
Slavko 做了一个不寻常的梦。在一个晴朗的早上,\(N\) 个白色的矩形一个接着一个爬上了 Slavko 家的屋顶,并在屋顶上晒太阳。每个矩形在屋顶都选定了一个位置,使得它的边与屋顶的棱角平行。有些矩形可能会覆盖在其它矩形所在的位置上。每个矩形的长、宽分别为 \(A_i,B_i\),其与屋顶左方和下方的棱角的距离分别为 \(X_i,Y_i\)。
日落后,矩形们从屋顶上下来,并睡了一觉。次日,它们发现,有些矩形变成了黄色,而有些仍为白色。变为黄色的矩形都是完全暴露在阳光下的。
请判断每个矩形是否变为了黄色。
输入格式
第一行输入正整数 \(N\),表示矩形的个数。
接下来的 \(N\) 行,每行输入整数 \(X_i,Y_i,A_i,B_i\)。输入顺序与登上屋顶的顺序一致。
输出格式
输出 \(N\) 行。其中,若第 \(i\) 个矩形变为黄色,则在第 \(i\) 行输出 DA,否则在该行输出 NE。
样例 #1
样例输入 #1
5
1 1 4 2
6 1 1 1
2 2 2 3
3 4 3 2
4 0 1 2
样例输出 #1
NE
DA
NE
DA
DA
样例 #2
样例输入 #2
3
3 3 1 1
2 2 3 3
1 1 5 5
样例输出 #2
NE
NE
DA
提示
样例 1 解释
矩形 \(1,3\) 没有完全暴露在阳光下,因而它们没有变为黄色:
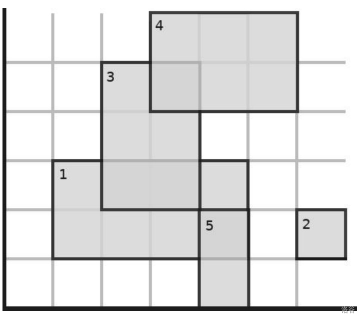
数据规模与约定
对于 \(10\%\) 的数据,\(N \le 10^4\)。
对于 \(100\%\) 的数据,\(1 \le N \le 10^5\),\(0 \le X_i,Y_i \le 10^9\),\(1 \le A_i,B_i \le 10^9\)。
说明
本题分值按 COCI 原题设置,满分 \(130\)。
题目译自 COCI2018-2019 CONTEST #2 T5 Sunčanje。
分析
我们记矩阵序列为 \(A\) ,其中 \(A[i]=(x_1,y_1,x_2,y_2)(x_1\le x_2,y1\le y_2)\) ,为了方便,我们将 \(A[i]\) 的 \(x_1\) 写作 \(A[i,x_1]\) ,其余类似
那么矩阵 \(i\) 被矩阵 \(j\) 覆盖需要满足以下条件
(在这里有一个细节,就是有可能一个矩形的右边和一个矩形的左边在同一直线上(亦或者一个矩形的上边和一个矩形的下边在同一直线上),但此时没有交点却仍然会被累加进入答案,故为了解决这个问题,可以把右上角整体缩一格,也即右上角的横纵坐标全部-1(这就是部分同志最后几个点过不了的原因));
考虑如何求解
这个玩意类似于偏序问题,考虑使用 CDQ 分治
若按照时间轴分治,则设分治两区间为 \([l,mid],[mid+1,r]\)
此时 \([l,mid]\) 的时间都早于 \([mid+1,r]\)
此时我们需要考虑后半区间对前半区间的影响,先用常规双指针套路维护限制条件 \(A[j,x_1]\le A[i,x_2]\)
将区间 \([l,mid]\) 按照 \(x_2\) 递增排序,区间 \([mid+1,r]\) 按照 \(x_1\) 递增排序,设两个指针分别为 \(L,R\)
采用双指针扫描,则 \([mid+1,R]\) 的矩形都满足对于 \(L\) 来说 \(A[L,x_2]\ge A[k,x_1]\) ,考虑判定在 \([mid+1,R]\) 中有无矩形可以覆盖 \(L\)
按照 \(CDQ\) 分治的套路我们需要数据结构来维护剩余的几个条件
这里由于限制条件就是要求矩形横向有交点,竖向有交点,而对于竖向有交点,可以转化为线段有交问题,考虑使用维护线段的数据结构——线段树
那,我们对区间 \([A[i,y_1],A[i,y_2]]\) 进行修改,只需要我们能够判定在区间 \([A[L,y_1],A[L,y_2]]\) 中有无大于等于 \(A[L,x_1]\) 的元素,这启发我们的线段树维护区间最大值,假设我们将区间 \([l',r']\) 的最大值记为 \(g[l',r']\) ,记 \(f[i]\) 表示第\(i\)个矩形是否被覆盖
那么就有 \(f[A[L,id]]|=A[L,x_1]\le g[A[L,y_1],A[L,y_2]]\)
统计完了之后将线段树全部清空为-1即可
最后,我们再来梳理一遍这个过程
- 离散化坐标
- 在CDQ分治中
- 左半区间按照\(x_2\)排,右半区间按\(x_1\)排
- 双指针扫描,使得\(A[L,x_2]\ge A[R,x_1]\)
- 在扫描的过程中不断在线段树的区间\([A[R,y_1],A[R,y_2]]\)上更新区间最大值
- 对于\(L\)查询区间\([A[L,x_1,x_2]]\)是否存在大于\(A[L,x_1]\)的值,存在也就表示\(L\)被覆盖
- 清空线段树
时间复杂度是\(O(n\log^2n)\),线段树常数大得一批,怪不得时间要求4s
#include<iostream>
#include<cstdio>
#include<algorithm>
#define scanf scanf_s
using namespace std;
#define N 1000050
struct node {
int id, x1, x2, y1, y2;
}a[N];//矩阵
int b[N], c[N], cnt;//离散化
int f[N], n, m;
struct seg_tree {
int mx, tag, lazy, l, r;
}t[N << 2];//线段树
#define lc x<<1
#define rc x<<1|1
void build(int l, int r, int x) {
t[x] = { 0,0,-1,l,r };
if (l == r)return;
int mid = l + r >> 1;
build(l, mid, lc);
build(mid + 1, r, rc);
}
inline void pushup(int x) {
t[x].mx = max(t[lc].mx, t[rc].mx);
}
inline void pushdown(seg_tree& a, seg_tree& b, seg_tree& c) {
if (a.lazy != -1) {
b.tag = c.tag = 0;
b.mx = c.mx = 0;
b.lazy = c.lazy = 0;
a.lazy = -1;
}
b.tag = max(b.tag, a.tag);
c.tag = max(c.tag, a.tag);
b.mx = max(b.mx, a.tag);
c.mx = max(c.mx, a.tag);
a.tag = 0;
return;
}
inline void pushdown(int x) {
pushdown(t[x], t[lc], t[rc]);
}
void update(int x, int l, int r, int k) {
if (l <= t[x].l && t[x].r <= r) {
t[x].mx = max(t[x].mx, k);
t[x].tag = max(t[x].tag, k);
return;
}
pushdown(x);
int mid = t[x].l + t[x].r >> 1;
if (l <= mid)update(lc, l, r, k);
if (mid < r)update(rc, l, r, k);
pushup(x);
}
int find(int x, int l, int r) {
if (l <= t[x].l && t[x].r <= r) {
// printf("%d %d %d %d %d\n", t[x].lazy, t[x].tag, t[x].l, t[x].r, t[x].mx);
return t[x].mx;
}
int ans = -1, mid = t[x].l + t[x].r >> 1;
pushdown(x);
if (l <= mid)ans = max(ans, find(lc, l, r));
if (mid < r)ans = max(ans, find(rc, l, r));
pushup(x);
return ans;
}
#undef lc
#undef rc
void init() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int A, B, c, d;
scanf("%d%d%d%d", &A, &B, &c, &d);
c += A - 1, d += B - 1;
a[i] = { i,A,c,B,d };
b[++cnt] = A, b[++cnt] = B, b[++cnt] = c, b[++cnt] = d;
}
sort(b + 1, b + cnt + 1);
cnt = unique(b + 1, b + cnt + 1) - b - 1;
// printf("%d\n", cnt);
for (int i = 1; i <= n; i++) {
a[i].x1 = lower_bound(b + 1, b + cnt + 1, a[i].x1) - b;
a[i].y1 = lower_bound(b + 1, b + cnt + 1, a[i].y1) - b;
a[i].x2 = lower_bound(b + 1, b + cnt + 1, a[i].x2) - b;
a[i].y2 = lower_bound(b + 1, b + cnt + 1, a[i].y2) - b;
// printf("%d %d %d %d\n", a[i].x1, a[i].y1, a[i].x2, a[i].y2);
}
}
bool cmp1(node a, node b) {
return a.x1 < b.x1;
}
bool cmp2(node a, node b) {
return a.x2 < b.x2;
}
void cdq(int l, int r) {
if (l == r)return;
int mid = l + r >> 1;
cdq(l, mid);
cdq(mid + 1, r);
int L = l, R = mid + 1;
sort(a + l, a + mid + 1, cmp2);
sort(a + R, a + r + 1, cmp1);
// for (int i = l; i <= r; i++)printf("%d ", a[i].id);
// puts("");
for (; L <= mid; L++) {
while (a[R].x1 <= a[L].x2 && R <= r) {
update(1, a[R].y1, a[R].y2, a[R].x2);
R++;
}
f[a[L].id] |= find(1, a[L].y1, a[L].y2) >= a[L].x1;
// if (find(1, a[L].y1, a[L].y2) >= a[L].x1) {
// printf("%d %d %d\n", a[L].id, find(1, a[L].y1, a[L].y2), L-l);
// }
}
t[1].tag = t[1].mx = t[1].lazy = 0;
pushdown(1);
// puts("Cleaded");
}
int main() {
init();
build(1, cnt << 1, 1);
cdq(1, n);
for (int i = 1; i <= n; i++) {
if (f[i])puts("NE");
else puts("DA");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号