分组——题解

分组

题目背景

大样例可在页面底部「附件」中下载。

题目描述

小 C 在了解了她所需要的信息之后，让兔子们调整到了恰当的位置。小 C 准备给兔子 们分成若干个小组来喂恰当的胡萝卜给兔子们吃。

此时， $n$ 只兔子按一定顺序排成一排，第 $i$ 只兔子的颜色是 $a_i$ 。由于顺序已经是被 调整好了的，所以每个小组都应当是序列上连续的一段。

在分组前，小 C 发现了一个规律：有些兔子会两两发生矛盾。并且，两只兔子会发生矛 盾，当且仅当代表他们的颜色的数值之和为一个正整数的平方。比如，1 色兔子和 2 色兔子 不会发生矛盾，因为 3 不是任何一个正整数的平方；而 1 色兔子却会和 3 色兔子发生矛盾， 因为 $4=2^2$。

小 C 认为，只要一个小组内的矛盾不要过大就行。因此，小 C 定义了一个小组的矛盾 值 $k$ ，表示在这个小组里，至少需要将这个组再一次分成 $k$ 个小团体；每个小团体并不需 要是序列上连续的一段，但是需要使得每个小团体内任意两只兔子之间都不会发生矛盾。

小 C 要求，矛盾值最大的小组的矛盾值 $k$ 不超过 $K$ 就可以了。当然，这样的分组方 法可能会有很多个；为了使得分组变得更加和谐，小 C 想知道，在保证分组数量最少的情况 下，字典序最小的方案是什么。你能帮帮她吗？

字典序最小的方案是指，按顺序排列分组的间隔位置，即所有存在兔子 $i$ 和 $i+1$ 在 不同组的位置 $i$，和其它所有相同分组组数相同的可行方案相比总有第一个不同的位置比其 它方案小的方案。

输入格式

从标准输入中读入数据。

输入第 1 行两个正整数 $n,K$。

输入第 2 行 $n$ 个正整数，第 $i$ 个数表示第 $i$ 只兔子的颜色 $a_i$。

输出格式

输出到标准输出中。

输出第 1 行一个正整数 $m$，为你至少需要将兔子分为多少个小组。

输出第 2 行$m-1$个从小到大的排列的正整数，第 $i$ 个数 $s_i$ 表示 $s_i$ 和 $s_i+1$ 在 你的方案里被分到了两个小组。如果 $m=1$，那么请输出一个空行。

样例 #1

样例输入 #1

5 2 
1 3 15 10 6

样例输出 #1

2
1

提示

【样例 1 解释】

如果将五只兔子全部分到同一个小组的话，那么 (1, 3) (3, 6) (6, 10) (10, 15) (1, 15) 均 不能分到同一个小团体；因为最多分成两个小团体，所以为了满足前 4 对限制，只能分为 {{1, 6, 15}, {3, 10}}，但此时不满足 (1, 15) ，所以不存在一种组数为 1 的方案满足全部限制。

如果将五只兔子分为两个小组的话，一种字典序最小的可行的分组方案是 {1}, {3, 15, 10, 6}，此时第二组内的小团体数量不超过 2 的一种分法是 {{3, 10}, {15, 6}}。

【数据范围】

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表：

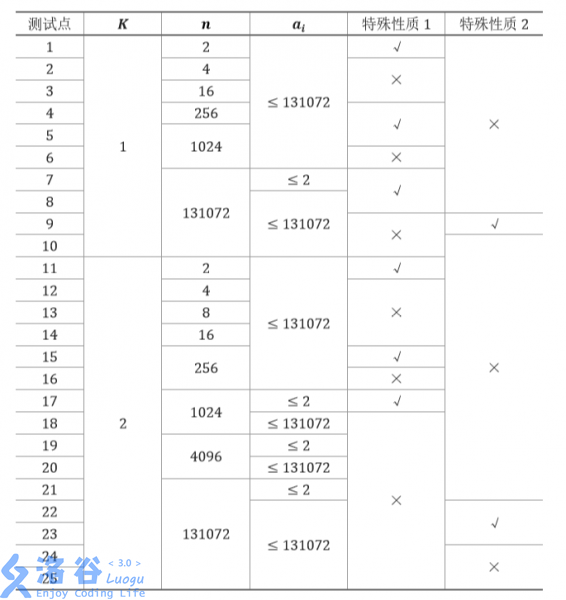
特殊性质 1：保证最优分组方案唯一。

特殊性质 2：保证不会有两只相同颜色的兔子。

题解

考虑观察数据范围:$\sqrt{2\times 131072}=512$.启发我们设计一个$O(N\sqrt{N})$的算法

发现$K\le 2$,所以完全可以分类讨论

K=1

当$K=1$的时候，变成了一个简化版问题：给定$n$个数，将其分成尽量少的段数，使得每一段内没有一对数的和为平方数

显然，如果区间$[l,r]$合法，那么$[l,r]$的任何子区间都是合法的，那么考虑每一次都取最长的一段。

要字典序最小的话，可以从后往前取，问题就变成了每一次求出最长段。

因为这个平方数最大为512，大不了可以枚举这个平方数，判断有无数可以与其配对。由于值域与$n$同级，那么可以开个桶$S$，$S_i=1/0$表示$i$是否在当前段出现过

具体的，每一可以在外层倒序循环$a_i$，在内部循环$[1,512]$的平方数$x$，判断$S_{x^2-a_i}$是否为1。如果为1的话说明得新开一段，此时将$S$清空，将$S_{a_i}$标记为1

如果扫描完了还没有发现一个为1，那么将$S_{a_i}$标记为1，继续扫描

K=2

此时大体思路一致，只是如何判断的问题。此时问题就变成了判断每一段是否可以被分为两个部分.

这个有点像关押罪犯那道题，可以用二分图（将平方数连边）或者扩展域/边带权并查集解决。

只是二分图的话，每次都要跑一边，可能会导致复杂度假掉，考虑并查集。因为扩展域好写，就写扩展域吧.设fa[1~n]为无矛盾域，f[n+1~n<<1]为矛盾域

那么具体在内层循环判断的时候，当然若$S_{x^2-a_i}$为$1$的话将两个的无矛盾域与矛盾域交叉合并。

当合并出现矛盾的时候，就需要重新重置f,S。当然别忘了都得给$S_{a_i}$打上标记。

这里有个细节，就是一个段内可能有重复出现的数字，而他们的域不一定相同.此时最好是将$S$的每个元素变成vector

需要注意的是，最好是维护一下当前段的起始位置，以便保证重置复杂度

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
#define N 350000
int f[N << 1], n, m, s1[N], a[N], g[N], cnt;
vector<int>s2[N];
int find(int x) {
	return x == f[x] ? x : f[x] = find(f[x]);
}
void merge(int x, int y) {
	x = find(x), y = find(y);
	f[x] = y;
}
void init() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
	if (!(m & 1))for (int i = 1; i <= n << 1; i++)f[i] = i;
}
int solve1() {
	int ans = 1, id = n;
	s1[a[n]] = 1;
	for (int i = n - 1; i; --i) {
		for (int j = 1; j <= 520; j++) {
			if (j * j - a[i] < 0)continue;
			if (s1[j * j - a[i]]) {
				ans++;
				for (int k = i; k <= id; k++)s1[a[k]] = 0;
				id = i;
				g[++cnt] = id;
				break;
			}
		}
		s1[a[i]] = 1;
	}
	return ans;
}
int solve2() {
	int ans = 1, id = n;
	s2[a[n]].push_back(n);
	for (int i = n - 1; i; --i) {
		for (int j = 1; j <= 520; j++) {
			if (j * j - a[i] < 0 || !s2[j * j - a[i]].size())continue;
			int len = s2[j * j - a[i]].size();
			for (int k = 0; k < len; k++) {
				merge(i + n, s2[j * j - a[i]][k]);
				merge(i, s2[j * j - a[i]][k] + n);
			}
		}
		if (find(i) == find(i + n)) {
			ans++;
			g[++cnt] = i;
			for (int k = i; k <= id; k++) {
				if (s2[a[k]].size())s2[a[k]].clear();
				f[k] = k, f[k + n] = k + n;
			}
			id = i;
		}
		s2[a[i]].push_back(i);
	}
	return ans;
}
int main() {
	init();
	if (m & 1)printf("%d\n", solve1());
	else printf("%d\n", solve2());
	for (int i = cnt; i; --i) {
		printf("%d ", g[i]);
	}
}