双栈排序——二分图+模拟

二分图建模-双栈排序

题目描述

Tom 最近在研究一个有趣的排序问题。如图所示，通过 \(2\) 个栈 \(S_1\) 和 \(S_2\)，Tom 希望借助以下 \(4\) 种操作实现将输入序列升序排序。

操作 \(a\)：将第一个元素压入栈 \(S_1\)。

操作 \(b\)：将 \(S_1\) 栈顶元素弹出至输出序列。

操作 \(c\)：将第一个元素压入栈 \(S_2\)。

操作 \(d\)：将 \(S_2\) 栈顶元素弹出至输出序列。

如果一个 \(1\sim n\) 的排列 \(P\) 可以通过一系列合法操作使得输出序列为 \((1,2,\cdots,n-1,n)\)，Tom 就称 \(P\) 是一个“可双栈排序排列”。例如 \((1,3,2,4)\) 就是一个“可双栈排序序列”，而 \((2,3,4,1)\) 不是。下图描述了一个将 \((1,3,2,4)\) 排序的操作序列：\(\texttt {a,c,c,b,a,d,d,b}\)。

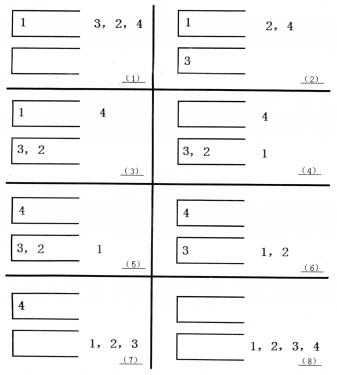
当然，这样的操作序列有可能有几个，对于上例 \((1,3,2,4)\)，\(\texttt{a,b,a,a,b,b,a,b}\) 是另外一个可行的操作序列。Tom 希望知道其中字典序最小的操作序列是什么。

输入格式

第一行是一个整数 \(n\)。

第二行有 \(n\) 个用空格隔开的正整数，构成一个 \(1\sim n\) 的排列。

输出格式

共一行，如果输入的排列不是“可双栈排序排列”，输出 0。

否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

样例 #1

样例输入 #1

4
1 3 2 4

样例输出 #1

a b a a b b a b

样例 #2

样例输入 #2

4
2 3 4 1

样例输出 #2

0

样例 #3

样例输入 #3

3
2 3 1

样例输出 #3

a c a b b d

提示

\(30\%\) 的数据满足：\(n\le10\)。

\(50\%\) 的数据满足：\(n\le50\)。

\(100\%\) 的数据满足：\(n\le1000\)。

2021.06.17 加强 by SSerxhs。hack 数据单独分为一个 subtask 防止混淆。

分析

首先来考虑单栈排序，不难发现，若使单栈排序无解，当且仅当

\(\exists i,j,k(i<j<k)，a_k<a_i<a_j\)

证明显然

那么由这个性质，不难发现\((i,j)\)构成顺序对，\((i,k),(j,k)\)构成逆序对，那么\(k\)就可以简单的处理，做一个后缀最小值即可判断\(i,j\)能否满足条件

那么我们将不能共存的\((i,j)\)连一条无向边，再做一个二分图，就可以判定是否可行了(在二分图的时候优先将编号小的节点划到\(S1\))并且划定集合

那么问题就变成了对两个栈进行单栈排序，模拟即可

需要注意的是，两个栈一定都单调的，于是为了保证字典序，我们可以在第二个栈必须出栈的时候再出

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<stack>
using namespace std;
#define N 50500
#define M 3000500
int tot,a[N],cnt,now,c[N],head[N],ver[N],nxt[N],f[N],n,m;
stack<int>s1,s2;
void add(int u,int v){
	nxt[++tot]=head[u],ver[head[u]=tot]=v;
}
void dfs(int u,int num){
	c[u]=num;
	for(int i=head[u];i;i=nxt[i]){
		int v=ver[i];
		if(!c[v])dfs(v,num==1?2:1);
		if(c[v]==c[u]){
			puts("0");
			exit(0); 
		}
	}
}
void init(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	f[n]=a[n];
	for(int i=n-1;i>0;i--)f[i]=min(f[i+1],a[i]);
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			if(a[i]<a[j]&&f[j]<a[i])
				add(i,j),add(j,i);
	for(int i=1;i<=n;i++)if(!c[i])dfs(i,1);
}
void solve(int x,int id){
	int flag=0;
	while(!flag){
		flag=1;
		while(!s1.empty()&&s1.top()==now+1){
			printf("b ");
			now++;
			flag=0;
			s1.pop();
		}
		if(x!=-1&&c[id]==1&&(s1.empty()||s1.top()>x)){	
			s1.push(x);
			printf("a ");
			break;
		}
		if(x!=-1&&c[id]==2&&(s2.empty()||s2.top()>x)){
			s2.push(x);
			printf("c ");
		}
		while(!s2.empty()&&s2.top()==now+1){
			printf("d ");
			now++;
			flag=0;
			s2.pop();
		}
	}
	if(x==-1)return ;
	
}
int main(){
	init();
	for(int i=1;i<=n;i++)solve(a[i],i);
	solve(-1,-1);
	return 0;
}