冰魄吐息题解

冰魄吐息

题目背景

\(\text{加强版}\Leftarrow\)

题目描述

\(N\) 个点，第 \(i\) 个点坐标为 \((x_i,y_i)\)。

定义一束激光：\(y=kx\)，若点 \(i\) 满足到该条直线距离 \(\le d\)，认为被激光击中。

求使用至多 \(K\) 束激光，击毁图中所有点的最小代价 \(d\)。

输入格式

第一行输入两个正整数 \(N,K\)。

第 \(2 \sim N+1\) 行，每行两个非负整数 \(x_i,y_i\)，表示第 \(i\) 个点的坐标。

输出格式

第一行输出最小代价 \(d\)，保留到小数点后 \(2\) 位。

样例 #1

样例输入 #1

2 1
2 3
6 3

样例输出 #1

1.20

样例 #2

样例输入 #2

4 3
1 6
4 6
4 2
4 0

样例输出 #2

0.97

提示

样例说明

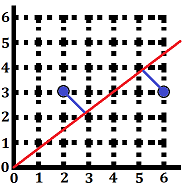
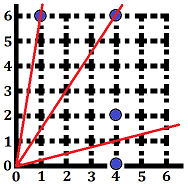
样例 \(\#1\) 中两蓝色点坐标分别为 \((2,3)\) 和 \((6,3)\)，到直线 \(y=\frac{3}{4}x\) 的距离均为 \(\frac{6}{5}=1.2\)，因此输出 1.20。	样例 \(\#2\) 中坐标为 \((4,0),(4,2)\) 的点与斜率为 \(\frac{1}{4}\) 的直线之间距离为 \(\frac{4}{17}\sqrt{17}\approx0.97014\dots\)，因此输出 0.97。

可以证明两个样例中的方案是最优的，因此所求的 \(d\) 是最小的。

提示

1. 可能会用到的公式：点 \((x_0,y_0)\) 到直线 \(y=kx\) 的距离是 \(\large\frac{|y_0-kx_0|}{\sqrt{k^2+1}}\)。
2. 对于 C++ 选手，建议使用 变量类型 long double 进行数值计算。
   输出时请用形如 printf("%.2Lf",ans) 的形式输出答案，注意 %.2Lf 中的 L 是大写。
3. 本题中存在的浮点数运算可能较多，虽然已经增大时限，但仍然请注意常数因子对程序效率的影响。

数据范围

本题采用捆绑测试。

记 \(M\) 为所有 \(x_i,y_i\) 的最大值。

Subtask	Score	\(M\le\)	\(K\le\)
\(1\)	\(30\)	\(10\)	\(1\)
\(2\)	\(30\)	\(1.5\times10^4\)	\(1\)
\(3\)	\(40\)

对于 \(100\%\) 的数据：\(1\le N,M,K\le2.5\times10^4\)。

所有数据均保证不存在相同的 \((x_i,y_i)\) 出现多次。

---

题解

根据题目，明显的有"最多的最少"这一醒目的词眼，简单分析可得本题具有单调性

那么考虑二分，容易想到，对于一个点能被击中，肯定是以此点为圆心，二分的值为半径的圆与直线有交点

进一步地，稍稍旋转一下，不难发现满足要求的直线的斜率肯定是被原点与此圆相切的两条直线的夹住，这时候分情况讨论

假设我们设圆心为\(p\),半径为\(r\)，\(p\)上方的切线记为\(l_1\),下方的切线记为\(l_2\)，斜率分别为\(k_1,k_2\)，先特殊处理切线为坐标系的情况

明显，为了击中更多的点，我们的直线都过一三象限肯定不会比其他决策差

1. 当\(0< k_1,k_2\)时，斜率在区间\([k_2,k_1]\)上的都可以与圆\(p\)相交
2. 当\(0<k_1，0>k_2\)的时候，此时\(l_2\)过二四象限，此时斜率在\([0,k_1]\)的直线都与圆相交，此时我们无需考虑\([k_2,0]\)的部分，因为射出一条斜率小于0的直线一定不优（因为点都在第一象限）
3. 当\(0>k_1,0<k_2\)的时候，此时\(l_1\)过二四象限，此时我们同样无需考虑\([k_1,0]\)的部分，只需要考虑\(k_2\)到无穷大的部分即可
4. 其余情况一三象限任意直线都可以击中

那么我们就可以使用二分法求出有效区间，对于\(k_1\)的二分直接以直线\((O,p)\)的斜率为下界，无穷大为上界即可，\(k_2\)则以直线\((O,p)\)的斜率为上界，0为下界二分即可

最终就可以得到每个点的有效斜率区间，此时问题转化为了给定\(n\)个区间，需要使用最少的点数使得每个区间至少有一个点。这是一个简单的贪心问题

贪心策略：将所有区间按右端点为第一关键字，左区间为第二关键字排序，则取点一定是在合法情况下尽量往右边取

证明：易知这样取点一定不会让结果变差，根据贪心的决策包容性，命题得证

那么做法就显然了，维护一个变量，表示最后一个点的位置，从1到n扫描，对于每一个区间，判定这个变量是否在区间内，如果不是在区间内，将点的数量加一，并且将变量更新为这个区间的右端点即可

这样我们就得到了最小直线使用数，判断这个数与\(K\)比较，便可知道二分的值如何变化了。
至此，本题便得到了解决

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
double n, m;
#define N 500050
//#define scanf scanf_s
#define eps 1e-8
#define inf 1e7
#define db double
struct node {
    db l, r;
}a[N], b[N];
bool cmp(node a, node b) {
    return a.r < b.r;
}
db dist(db k, double x, double y) {
    return fabs(y - k * x) / sqrt(k * k + 1);
}
node erfen(double x, double y, db d) {
    node ans = { 0.0,0.0 };
    db l, r;
    if (fabs(x) < eps)return { -y / d,y / d };
    l = y / x, r = inf;//先分上层
    while (l + eps < r) {
        db mid = (l + r) * 0.5;
        if (dist(mid, x, y) <= d) {
            l = mid;
        }
        else r = mid;
    }
    ans.r = l;
    l = 0, r = y / x;
    while (l + eps < r) {
        db mid = (l + r) * 0.5;
        if (dist(mid, x, y) <= d) {
            r = mid;
        }
        else l = mid;
    }
    ans.l = l;
    return ans;
}
double check(db d) {
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (a[i].l * a[i].l + a[i].r * a[i].r <= d) {
            continue;
        }
        else b[++cnt] = erfen(a[i].l, a[i].r, d);
    }
    sort(b + 1, b + cnt + 1, cmp);
    double ans = 0;
    db pos = -inf;
    for (int i = 1; i <= cnt; i++) {
        if (pos <= b[i].l)pos = b[i].r, ans++;
    }
    return ans;
}
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].l >> a[i].r;
    }
    db l = 0, r = inf, e = 1e-5, ans = 0;
    while (l + e < r) {
        db mid = (l + r) * 0.5;
        if (check(mid) > m)l = mid;
        else r = mid;
    }
    printf("%.2f", r);
}