2019牛客暑期多校训练营（第十场）E-Hilbert Sort（分形）

>传送门<

题意

---

现给出你 $n $个坐标和 $k$，让你根据$ k$阶 希尔伯特曲线的走向排列给出的 $n $个坐标

希尔伯特曲线如下：

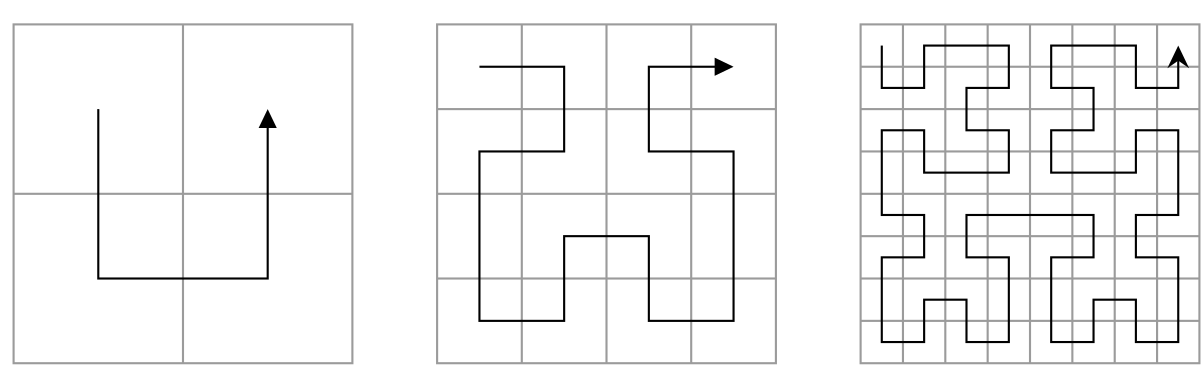
　　　　　 $k=1$　　　　　　　　　　 $k=2$　　　　　　　　　　 $k=3$
可以将边长为 $2^{k}$ 的正方形平分成四部分：①左上角②左下角③右下角④右上角

$k $阶希尔伯特曲线可由$ k-1 $阶希尔伯特曲线推出；

　（1）$k-1 $阶希尔伯特曲线按照主对角线反转得到①部分；

　（2）$k-1$ 阶希尔伯特曲线拷贝到②③部分；

　（3）$k-1 $阶希尔伯特曲线按照副对角线反转得到④部分；

如上图所示，分别表示 1阶，2阶，3阶 希尔伯特曲线

分析

---

定义好比较函数后直接调用排序算法即可。

希尔伯特曲线本来就是用于二维到一维的映射的，因此我们可以考虑对于每一个点预处理出它是希尔伯特曲线上第几个经过的，然后排序。

可以看出，假设在方阵的中心设立一个原点，那么希尔伯特曲线依次经过原点的左上，左下，右下，右上，而这四个象限希尔伯特函数的轨迹是互相对称的，对于不同的象限，首先算出它前面经过的象限的总点数，然后将两个点的相对坐标做不同的对称变换后，递归到小一号的希尔伯特曲线中继续。

实际中题目中建立的坐标系是这样的（我在这里栽了个大坑，怪不得怎么看都不对劲）

 

Code（这个没有那么简洁，但可读性更高）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6+5;
struct node{
    ll x, y, f;
    bool operator<(const node& a)const{
        return f<a.f;
    }
}p[maxn];
 
int f(ll k,ll x,ll y){
    if(k==0) return 1;
    ll n = 1<<(k-1);
    if(x<=n){
        if(y<=n)return f(k-1,y,x);
        y-=n; return f(k-1,n-y+1,n-x+1)+n*n*3;
    }else{x-=n;
        if(y<=n)return f(k-1,x,y)+n*n;
        y-=n;return f(k-1,x,y)+n*n*2;
    }

}

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n; i++){
        scanf("%lld%lld", &p[i].x, &p[i].y);
        p[i].f = f(k,p[i].x,p[i].y);
    }
    sort(p, p+n);
    for(int i = 0; i < n; i++) printf("%lld %lld\n", p[i].x, p[i].y);
    return 0;
}