图

图的相关术语

图是网络结构的抽象模型。图是一组由边连接的节点（或定点）。

一个图 G = (V, E) 由以下元素组成：

• V：一组顶点
• E：一组边，连接 V 中的顶点

图示：

相邻顶点：由一条边连接在一起的顶点。比如，A 和 B 是相邻的，A 和 E 不是相邻的。

度：一个顶点的度是其相邻顶点的数量。比如，A 和其他3个顶点相连接，因此 A 的度为 3。

路径：路径是顶点v₁, v₂, ……, v_k 的一个连续序列_，其中  v_i 和 v_i+1 是相邻的。比如，上图中包含路径 ABEI 和 ADH。简单路径要求不包含重复的顶点。

环：环是一个简单路径，比如 ADCA（最后一个顶点重新回到 A）。

如果图中不存在环，则称改图是无环的。如果图中每两个顶点间都存在路径，则该图是连通的。

有向图和无向图

图可以是无向的（边没有方向）或是有向的（有向图）。

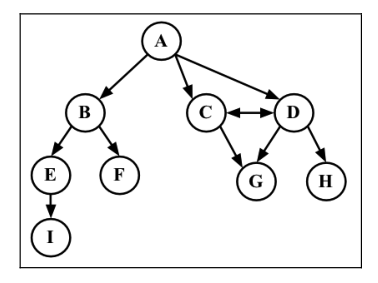
如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。例如，C 和 D 是强连通的，而 A 和 B 不是强连通的。

图还可以是未加权的或是加权的。

图的表示

1.邻接矩阵

图最常见的实现是邻接矩阵。每个节点都和一个整数相关联，该整数将作为数组的索引。用一个二维数组来表示顶点之间的连接。如果索引为 i 的节点和索引为 j 的节点相邻，则 array[i][j] === 1，否则 array[i][j] === 0。如下图所示。

不是强连通的图（稀疏图）如果用连接矩阵来表示，则矩阵中将会有很多0，这意味着浪费了计算机存储空间来表示根本不存在的边。邻接矩阵表示法不够好的另一个理由是，图中顶点的数量可能会变，而二维数组不太灵活。

2.邻接表

邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结。可以用列表（数组）、链表，甚至是散列表或是字典来表示相邻顶点列表。下图展示了邻接表数据结构。

3.关联矩阵

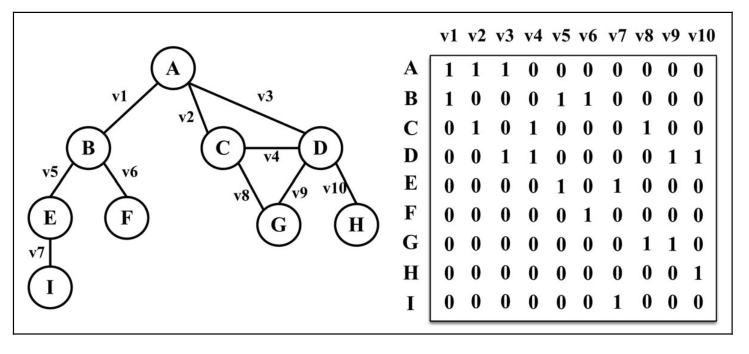
在关联矩阵中，矩阵的行表示顶点，列表示边。如下图所示，使用二维数组来表示两者之间的连通性，如果顶点 v 是边 e 的入射点，则 array[v][e] === 1；否则 array[v][e] === 0。关联矩阵通常用于边的数量比顶点多的情况，以节省空间和内存。

创建 Graph 类

class Graph {
    constructor(isDirected = false) {  //构造函数可以接受一个参数来表示图是否有向，默认情况下，图是无向的。
        this.isDirected = isDirected;
        this.vertices = [];   //使用一个数组来存储图中的所有顶点
        this.adjList = new Dictionary();  //字典来存储邻接表。字典使用顶点的名字作为键，邻接顶点列表作为值
    }
    
    addVertex(v) {   //向图中添加一个新顶点
        if(!this.vertices.includes(v)) {
            this.vertices.push(v);
            this.adjList.set(v, []);
        }
    }
    
    addEdge(v, w) {  //添加顶点之间的边，这个方法接收两个参数，即我们要建立连接的两个顶点。
        if(!this.adjList.get(v)) {
            this.addVertex(v);
        }
        if(!this.adjList.get(w)) {
            this.addVertex(w);
        }
        this.adjList.get(v).push(w);
        if(!this.isDirected) {  //如果 isDirected = true,则为有向图。否则，为无向图。
            this.adjList.get(w).push(v);
        }
    }
    
    getVertices() {  //返回顶点列表
        return this.vertices;
    }
    
    getAdjList() {  //返回邻接表
       return this.adjList;
    }

    toString() {
        let s = ' ';
        for(let i=0; i<this.vertices.length; i++) {
            s += `${this.vertices[i]}  -> `;
            const neighbors = this.adjList.get(this.vertices[i]);
            for(let j=0; j<neighbors.length; j++) {
                s += `${neighbors[j]} `;
            }
            s += '\n';
        }
        return s;
    }
}

//测试
const graph = new Graph();
const myVertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I'];
for(let i = 0; i<myVertices.length; i++) {
    graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');

console.log(graph.toString());

图的遍历

有两种算法可以对图进行遍历：广度优先遍历（breadth-first search, BFS）和深度优先遍历（depth-first search, DFS）。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环。

图遍历算法的思想是必须追踪每个第一次访问的节点，并且追踪有哪些节点没有被完全探索。对于两种图遍历算法，都需要明确指出第一个被访问的顶点。完全探索一个顶点要求我们探查该顶点的每一条边。对于每一条边所连接的没有被访问过的顶点，将去标注为被发现的，并将其加进待访问顶点列表中。

为了保证算法的效率，务必访问每个顶点至多两次。连通图中每条边和顶点都会被访问到。

用3种颜色来标注每个顶点的状态：

• 白色：表示该顶点还没有被访问
• 灰色：表示该顶点被访问过，但并未被探索过
• 黑色：表示该顶点被访问过且被完全探索过

使用 Colors 变量来标记顶点的颜色

const Colors = {
    WHITE: 0,
    GREY: 1,
    BLACK: 2
}

使用 initializeColor 方法来初始化每个顶点的颜色。在算法的开头，将所有的顶点标记为白色（未访问）。

const initializeColor = vertices => {
    const color = {};
    for(let i=0; i<vertices.length; i++) {
        color[vertices[i]] = Colors.WHITE
    }
    return color;
}

1.广度优先搜索

广度优先搜索算法会从指定的第一个顶点开始遍历图，先访问其所有的邻点（相邻顶点），就像一次访问图的一层。换句话说，就是先宽后深地访问顶点，如下图所示：

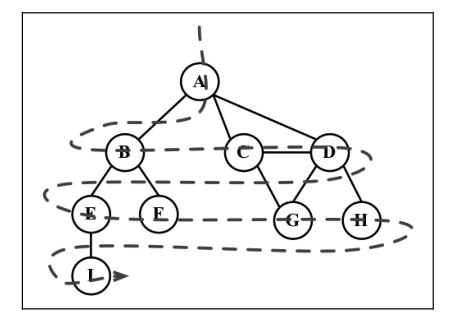
从顶点 v 开始的广度优先搜索算法实现的步骤：

1. 创建一个队列 Q。
2. 标注 v 为被发现的（灰色），并将 v 将入队列 Q。
3. 如果 Q 非空，则运行以下步骤：