【题意分析】
给你一张特殊的,被称为“轮状基”的无向图,求其生成树个数。
【解题思路】
引理:
基尔霍夫矩阵=度数矩阵-邻接矩阵(邻接矩阵权=两点连边数)
对于任意一个无向图,其生成树个数为其基尔霍夫矩阵的任意一个余子式的行列式值。
算法一:
直接暴力构图,用Matrix-Tree定理算出生成树个数,复杂度O(n3),理论可过,但考虑到高精度。。
附上一个算矩阵行列式的小公举工具。
算法二:
听说这个图很特殊,那一定有一些特殊性质?
先写出这个基尔霍夫矩阵的一般形态:

答案就是他的任意一个代数余子式的行列式值,为了最简化问题,我们可以去掉第一行第一列:

那么只要求这个矩阵的行列式值就可以了。
我们先初等变换一下:

这样答案就等于这个矩阵的行列式值前面加个符号,即乘上(-1)n-1
寻找这个矩阵行列式计算的规律,发现对倒数第二行进行高斯消元:
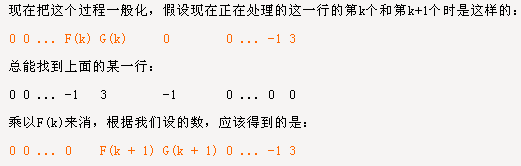
可得递推式组:
- Fi=Gi-1+3*Fi-1
- Gi=-Fi-1
整理后即Fi=3*Fi-1-Fi-2(边界F1=-1,F2=-3)
于是可以矩阵可以变换为这种形式:
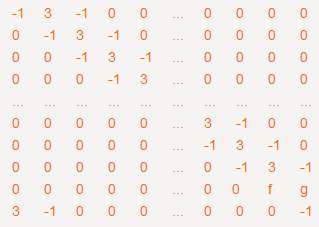
同理,对倒数第一行进行高斯消元,矩阵最终变为:

其行列式为:(-1)n-2*f*(i-g*h/f)=(-1)n-2*(f*i-g*h)
则原行列式值为:(-1)2n-3*(f*i-g*h)=g*h-f*i
带入各函数,结合关于行列式的FH定理,展开得:Hn+Fn-1-2
设原式=Rn,可得递推式:Rn=3*Rn-1-Rn-2+2(R1=2,R2=5)
这就是答案递推式了,复杂度O(n)。
恩,更详尽的证明,让vfk带你飞!
算法三:
打表找规律!(听说这就是我当初把这题当成高精度练习题的理由)
设Fi=3*Fi-2-Fi-4,则当i为奇数时,ansi=Fi2,当i为偶数时,ansi=5*Fi2
复杂度O(n)
【参考程序】
//听说我写这题时我还没有听说过一个叫做Py的东西。。QAQ
//这个板子还有可能是错的。。QAQ

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<string> 5 #include<algorithm> 6 #include<stack> 7 #define REP(I,start,end) for(int I=start;I<=end;I++) 8 #define PER(I,start,end) for(int I=start;I>=end;I--) 9 using namespace std; 10 long long digiter=100000000ll; 11 inline void init(long long initer) 12 { 13 digiter=initer; 14 } 15 struct bigNumber 16 { 17 int len; 18 long long num[501]; 19 inline void operator =(long long T) 20 { 21 memset(num,0,sizeof(num)); 22 len=0; 23 while(T) 24 { 25 num[++len]=T%digiter; 26 T/=digiter; 27 } 28 } 29 bool positive() 30 { 31 return len&&num[len]>0; 32 } 33 bool odd() 34 { 35 return num[1]&1; 36 } 37 inline bool operator ==(const bigNumber& T)const 38 { 39 if(len!=T.len) 40 return false; 41 REP(i,1,len) 42 if(num[i]!=T.num[i]) 43 return false; 44 return true; 45 } 46 inline bool operator >(const bigNumber& T)const 47 { 48 if(len<T.len) 49 return false; 50 if(len>T.len) 51 return true; 52 PER(i,len,1) 53 { 54 if(num[i]<T.num[i]) 55 return false; 56 if(num[i]>T.num[i]) 57 return true; 58 } 59 return false; 60 } 61 inline bool operator >=(const bigNumber& T)const 62 { 63 if(len<T.len) 64 return false; 65 if(len>T.len) 66 return true; 67 PER(i,len,1) 68 { 69 if(num[i]<T.num[i]) 70 return false; 71 if(num[i]>T.num[i]) 72 return true; 73 } 74 return true; 75 } 76 inline bool operator <(const bigNumber& T)const 77 { 78 if(len>T.len) 79 return false; 80 if(len<T.len) 81 return true; 82 PER(i,len,1) 83 { 84 if(num[i]>T.num[i]) 85 return false; 86 if(num[i]<T.num[i]) 87 return true; 88 } 89 return false; 90 } 91 inline bool operator <=(const bigNumber& T)const 92 { 93 if(len>T.len) 94 return false; 95 if(len<T.len) 96 return true; 97 PER(i,len,1) 98 { 99 if(num[i]>T.num[i]) 100 return false; 101 if(num[i]<T.num[i]) 102 return true; 103 } 104 return true; 105 } 106 inline void operator +=(const long long TT) 107 { 108 long long T=TT; 109 int i=1; 110 while(T) 111 { 112 num[i]+=T%digiter; 113 T/=digiter; 114 i++; 115 } 116 REP(i,1,len) 117 { 118 num[i+1]+=num[i]/digiter; 119 num[i]%=digiter; 120 } 121 while(num[len+1]) 122 len++; 123 } 124 inline void operator -=(const long long TT) 125 { 126 long long T=TT; 127 int i=1; 128 while(T) 129 { 130 num[i]-=T%digiter; 131 T/=digiter; 132 i++; 133 } 134 REP(i,1,len) 135 while(num[i]<0ll) 136 { 137 num[i+1]--; 138 num[i]+=digiter; 139 } 140 while(len&&num[len]==0ll) 141 len--; 142 } 143 inline void operator *=(const long long T) 144 { 145 REP(i,1,len) 146 num[i]*=T; 147 REP(i,1,len) 148 { 149 num[i+1]+=num[i]/digiter; 150 num[i]%=digiter; 151 } 152 while(num[len+1]) 153 { 154 len++; 155 num[len+1]+=num[len]/digiter; 156 num[len]%=digiter; 157 } 158 } 159 inline void operator /=(const long long T) 160 { 161 long long rest=0ll; 162 PER(i,len,1) 163 { 164 rest=rest*digiter+num[i]; 165 num[i]=rest/T; 166 rest%=T; 167 } 168 while(len&&num[len]==0ll) 169 len--; 170 } 171 }f[101],three; 172 inline bigNumber operator +(const bigNumber A,const bigNumber B) 173 { 174 bigNumber C; 175 memset(C.num,0,sizeof(C.num)); 176 C.len=max(A.len,B.len); 177 REP(i,1,C.len) 178 C.num[i]=A.num[i]+B.num[i]; 179 REP(i,1,C.len) 180 { 181 C.num[i+1]+=C.num[i]/digiter; 182 C.num[i]%=digiter; 183 } 184 while(C.num[C.len+1]) 185 { 186 C.len++; 187 C.num[C.len+1]+=C.num[C.len]/digiter; 188 C.num[C.len]%=digiter; 189 } 190 return C; 191 } 192 inline bigNumber operator -(const bigNumber A,const bigNumber B) 193 { 194 bigNumber C; 195 memset(C.num,0,sizeof(C.num)); 196 C.len=max(A.len,B.len); 197 REP(i,1,C.len) 198 C.num[i]=A.num[i]-B.num[i]; 199 REP(i,1,C.len) 200 while(C.num[i]<0) 201 { 202 C.num[i+1]--; 203 C.num[i]+=digiter; 204 } 205 while(C.len&&C.num[C.len]==0) 206 C.len--; 207 return C; 208 } 209 inline bigNumber operator *(const bigNumber A,const bigNumber B) 210 { 211 bigNumber C; 212 memset(C.num,0,sizeof(C.num)); 213 C.len=A.len+B.len-1; 214 REP(i,1,A.len) 215 REP(j,1,B.len) 216 { 217 C.num[i+j-1]+=A.num[i]*B.num[j]; 218 C.num[i+j]+=C.num[i+j-1]/digiter; 219 C.num[i+j-1]%=digiter; 220 } 221 while(C.num[C.len+1]) 222 { 223 C.len++; 224 C.num[C.len+1]+=C.num[C.len]/digiter; 225 C.num[C.len]%=digiter; 226 } 227 while(C.num[C.len]==0) 228 C.len--; 229 return C; 230 } 231 inline long long operator %(const bigNumber A,const long long B) 232 { 233 long long T=0; 234 PER(i,A.len,1) 235 T=(T*digiter+A.num[i])%B; 236 return T; 237 } 238 inline bigNumber gcd(const bigNumber AA,const bigNumber BB) 239 { 240 bigNumber C,A=AA,B=BB; 241 while(B.positive()) 242 { 243 C=A; 244 while(C>=B) 245 C=C-B; 246 A=B; 247 B=C; 248 } 249 return A; 250 } 251 inline bigNumber sqr(const bigNumber T) 252 { 253 return T*T; 254 } 255 inline bigNumber power(const bigNumber A,const int B) 256 { 257 stack<bool> isODD; 258 while(!isODD.empty()) 259 isODD.pop(); 260 int tmp=B; 261 while(tmp) 262 { 263 isODD.push(tmp&1); 264 tmp>>=1; 265 } 266 bigNumber C; 267 C=1ll; 268 while(!isODD.empty()) 269 { 270 C=sqr(C); 271 if(isODD.top()) 272 C=C*A; 273 isODD.pop(); 274 } 275 return C; 276 } 277 inline bigNumber fact(int n) 278 { 279 bigNumber ans; 280 ans=1ll; 281 REP(i,2,n) 282 ans*=i; 283 return ans; 284 } 285 inline bigNumber max(const bigNumber A,const bigNumber B) 286 { 287 if(A>B) 288 return A; 289 return B; 290 } 291 inline bigNumber min(const bigNumber A,const bigNumber B) 292 { 293 if(A<B) 294 return A; 295 return B; 296 } 297 inline void scan(bigNumber& T) 298 { 299 memset(T.num,0,sizeof(T.num)); 300 if(digiter==10ll) 301 { 302 T.len=0; 303 char ch=getchar(); 304 while(ch<'0'||ch>'9') 305 ch=getchar(); 306 while(ch>='0'&&ch<='9') 307 { 308 T.num[++T.len]=ch-'0'; 309 ch=getchar(); 310 } 311 REP(i,1,T.len>>1) 312 swap(T.num[i],T.num[T.len-i+1]); 313 } 314 else 315 { 316 string st; 317 cin>>st; 318 T.len=1; 319 long long tmp=1ll; 320 PER(i,st.length()-1,0) 321 { 322 T.num[T.len]+=(st[i]-'0')*tmp; 323 tmp*=10ll; 324 if(tmp==digiter) 325 { 326 T.len++; 327 tmp=1ll; 328 } 329 } 330 if(tmp==1ll) 331 T.len--; 332 } 333 } 334 inline void print(const bigNumber T) 335 { 336 if(T.len==0) 337 { 338 putchar('0'); 339 return; 340 } 341 if(digiter==10ll) 342 PER(i,T.len,1) 343 putchar(char(T.num[i])+'0'); 344 else 345 { 346 printf("%lld",T.num[T.len]); 347 PER(i,T.len-1,1) 348 { 349 long long tmp=digiter/10ll; 350 while(tmp) 351 { 352 printf("%lld",T.num[i]/tmp%10ll); 353 tmp/=10ll; 354 } 355 } 356 } 357 } 358 int n; 359 int main() 360 { 361 scanf("%d",&n); 362 f[1]=1ll; 363 f[2]=1ll; 364 f[3]=4ll; 365 f[4]=3ll; 366 three=3ll; 367 REP(i,5,n) 368 f[i]=f[i-2]*three-f[i-4]; 369 f[n]=sqr(f[n]); 370 if(~n&1) 371 f[n]*=5ll; 372 print(f[n]); 373 return 0; 374 }
和Py比较一下。。

1 if __name__=="__main__": 2 n,last,ans=input(),1,5 3 if n<2: 4 print 2 5 else: 6 for i in xrange(n-2): 7 ans,last=3*ans-last+2,ans 8 print ans
QAQ




 浙公网安备 33010602011771号
浙公网安备 33010602011771号