2024.10.17~19 杂题
杂题
AcWing5728. 截取子串
一眼 dp,令 \(f[i]\) 表示考虑到第 \(i\) 位的答案。
由于要求方案数,要么加法原理,要么乘法原理。
观察样例二,用乘法原理可以解释但是很难扩展到 \(f\) 上,所以考虑加法原理。对于样例二,每一个位置字母都一样,不难发现 \(f[3]=f[1]+f[2]\)。
考虑将其一般化,对于位置 \(j\),\(j+1\) 开始数 \(m\) 个字母且不超过 \(n\) 的情况下匹配到字符串 \(t\),以此为分界,显然对于前 \(j\) 个位置我们是可以随便选的。也就是说 \(f_i = \sum_{k=1}^{j}f_k\)。开一个前缀和数组维护 \(\sum f\) ,判断字符串是否相同 KMP 和哈希都可以。
复杂度 \(O(n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std ;
const int N = 1e5 + 5;
const int P = 131;
const int mod = 1e9 + 7;
int n, m;
char c[N], t[N];
unsigned long long p[N], h[N];
unsigned long long p2[N], h2[N];
int f[N], s[N];
unsigned long long calc(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1] ;
}
unsigned long long calc2(int l, int r)
{
return h2[r] - h2[l - 1] * p2[r - l + 1];
}
signed main()
{
cin >> (c + 1);
cin >> (t + 1);
n = strlen(c + 1), m = strlen(t + 1) ;
p[0] = 1;
for (rint i = 1; i <= n; i++)
{
p[i] = p[i - 1] * P;
h[i] = h[i - 1] * P + c[i];
p2[i] = p2[i - 1] * P;
h2[i] = h2[i - 1] * P + t[i];
}
unsigned long long hash_t = calc2(1, m);
f[0] = 1, s[0] = 1;
for (rint i = 1, j = -1; i <= n ; i++)
{
if (i >= m && calc(i - m + 1, i) == hash_t) j = i - m;
f[i] = ((j != -1 ? s[j] : 0ll) + f[i - 1]) % mod;
s[i] = (s[i - 1] + f[i]) % mod;
}
cout << (f[n] - 1 + mod) % mod << endl;
return 0 ;
}
AcWing5729. 闯关游戏
这道题的算法已经很显然了。
"按照自己喜欢的顺序,将它们全部通关",“\(n≤18\)”
考虑状态压缩 dp,\(f[i]\) 表示当前通关顺序 \(1\) 表示通关 \(0\) 表示未通二进制下的情况为 \(i\) 的总得分最大可能值。发现转移时需要枚举关卡节点只有这个状态无法维护,那么 \(f[i][j]\) ,\(j\) 表示最后一次选的关卡。那么转移就显然了,对于当前的 \(f_{i,j}\)
最后统计答案时,如果 \(i\) 中选择了 \(m\) 个关卡。就更新答案。取最大值。
复杂度 \(O(2^n n^2)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e1 + 9;
const int M = 1 << N;
int n, m, k;
int f[M][N];
int a[N];
int dist[N][N];
signed main()
{
cin >> n >> m >> k;
for (rint i = 0; i < n; i++) cin >> a[i];
for (rint i = 1; i <= k; i++)
{
int x, y, c;
cin >> x >> y >> c;
dist[x - 1][y - 1] = c;
}
for (rint i = 0; i < n; i++) f[1 << i][i] = a[i];
for (rint i = 0; i < 1 << n; i++)
for (rint j = 0; j < n; j++)
for (rint k = 0; k < n; k++)
if ((i >> j & 1) && (i >> k & 1) && (j != k))
//j,k∈i
f[i][j] = max(f[i][j], f[i - (1 << j)][k] + dist[k][j] + a[j]);
int ans = 0;
for (rint i = 0; i < 1 << n; i++)
{
int cnt = 0;
for (rint k = 0; k < n; k++) if (i >> k & 1) cnt++;
if (cnt != m) continue;
for (rint j = 0; j < n; j++) ans = max(ans, f[i][j]);
}
cout << ans << endl;
return 0;
}
AcWing5577. 有效图
结论:对于一个联通块,一定是完全连通图
假设只有两个点,显然
假设只有三个点,显然
假设只有四个点,先把三个点完全图画出来,再随便画出来一个点跟三个点中任意一个点连接,根据题目有效图的性质,把剩下的边也连出来,你会发现,它就是一个完全连通图。
所以维护每一个联通块的度数(其边数等于度数)以及点的个数 \(s\),如果 \(d = s \times (s - 1) /2\),那么就是对的,否则就是错的。
复杂度 \(O(n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e6 + 5;
int n, m;
int fa[N], s[N], d[N];
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
bool check()
{
for (rint i = 1; i <= n; i++)
if (fa[i] == i)
if (d[i] != (s[i] - 1) * s[i])
return 0;
return 1;
}
signed main()
{
cin >> n >> m;
for (rint i = 1; i <= n; i++) fa[i] = i, s[i] = 1;
for (rint i = 1; i <= m; i++)
{
int x, y;
cin >> x >> y;
x = find(x), y = find(y);
d[x]++, d[y]++;
if (x == y) continue;
s[y] += s[x], d[y] += d[x];
fa[x] = y;
}
if (check()) puts("YES");
else puts("NO");
return 0;
}
Pjudge.21792 抉择
显然有一个暴力 dp,设 \(f[i]\) 表示考虑到第 \(i\) 位的答案。显然有转移:
复杂度 \(O(n^2)\) 的,考虑优化,有一个假的想法,就是对于数据范围较大的时候,一定会选尽可能多的数。所以在枚举 \(j\) 的时候,起点设置为 \(max(i-50, 0)\)。复杂度降到了 \(O(nK)\),\(K≤50\)。但是有一个数据点过不了。
我们把原来第二层枚举从枚举下标改为枚举二进制位数,如果 (a[i] >> j) & 1,那么这个位置一定不会劣。记录当前位置 \(p[j]\)。在 dp 的时候把 \(a_j\) 换成 \(a_{p_j}\) 即可
复杂度 \(O(nK)\),\(K≤50\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 5;
int n, p[100];
int a[N], ans, f[N];
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
{
cin >> a[i];
f[i] = 0;
for (rint j = 45; j >= 0; j--)
{
int y = p[j];
f[i] = max(f[i], f[y] + (a[y] & a[i]));
if ((a[i] >> j) & 1) p[j] = i;
}
ans = max(ans, f[i]);
}
cout << ans << endl;
return 0;
}
Pjudge.21793 重生
显然答案是有单调性的,所以可以二分答案。判断当前答案是否可以完成所有任务。
首先有个很显然的结论,由于完成一个任务最少用一天,而深入思考代价也是一天,那么深入思考一定更优。那么在 check 的时候,维护三个变量 sum, cnt, res。如果 \(x>⌊\frac{t_i}{d_i}⌋\),\(sum +=⌊\frac{t_i}{d_i}⌋\),没必要使用深入思考。如果 \(x≤⌊\frac{t_i}{d_i}⌋\),\(cnt++\),因为这个任务要使用深入思考解决,res += max(0ll, t[i] - x * d[i])。最后判断条件为当天和全过程是否满足条件,即 cnt + res <= c 并且 sum + cnt + res <= (x - 1) * (c - cnt) + c。第二句判断标准就是开头说的,深入思考一定优,所以 \(x-1\) 次深思。
复杂度 \(O(n \log n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 5;
int n, c;
int t[N], d[N];
bool check(int x)
{
int sum = 0, cnt = 0, res = 0;
for (rint i = 1; i <= n; i++)
{
if (x > ceil(1.0 * t[i] / d[i]))
{
sum += ceil(1.0 * t[i] / d[i]);
}
else
{
cnt++;
res += max(0ll, t[i] - x * d[i]);
}
}
return cnt + res <= c && sum + cnt + res <= (__int128)(x - 1) * (c - cnt) + c;
}
signed main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> c;
for (rint i = 1; i <= n; i++) cin >> t[i] >> d[i];
int l = 1, r = 1e18;
while (l < r)
{
int mid = (l + r) >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << r - 1 << endl;
}
return 0;
}
Pjudge.21794 遍历
省流:NOIP Round #6 中真正的签到题
真的感觉这个题比前两个简单多了,不用脑子基本。
Tarjan 点双一下,记录块的大小,然后分类讨论两种不同的情况。
-
- 如果 \(y\) 在 \(x\) 子树里:
答案为 \(y\) 的第 \(d_x-d_y-1\) 级祖先的 \(size\) - \(y\) 的 \(size\) 再加 \(2\),之所以加二是因为题干里说了包括 \(x,y\)
-
- 如果 \(y\) 不在 \(x\) 子树里:
那么只要不在 \(x,y\) 所属块的点都能走,所以答案为 \(n-size_x-size_y + 2\)
代码实现上写个 Tarjan 再写个求 k 级祖先就可以了
复杂度 \(O(n \log n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 5;
int n, m, cnt;
int dfn[N], low[N];
int num, fa[N][21], stk[N], top;
vector<int> e[N], g[N];
int sz[N], d[N];
int in[N], out[N], tot;
void tarjan(int x, int father)
{
dfn[x] = low[x] = ++num;
stk[++top] = x;
for (rint y : e[x])
{
if (y == father) continue;
if (!dfn[y])
{
tarjan(y, x);
low[x] = min(low[x], low[y]);
if (low[y] >= dfn[x])
{
cnt++;
int z;
g[x].push_back(cnt);
fa[cnt][0] = x;
do
{
z = stk[top--];
g[cnt].push_back(z);
fa[z][0] = cnt;
} while (z != y);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
void dfs(int x, int father)
{
sz[x] = (x <= n);
in[x] = ++tot;
d[x] = d[father] + 1;
for (rint i = 1; i <= 19; i++) fa[x][i] = fa[fa[x][i - 1]][i - 1];
for (rint y : g[x])
{
if (y == father)continue;
dfs(y, x);
sz[x] += sz[y];
}
out[x] = tot;
}
int _rank(int x, int k)
{
for (rint i = 0; i <= 19; i++)
if (k >> i & 1)
x = fa[x][i];
return x;
}
int get(int x, int y)
{
return _rank(x, d[x] - d[y] - 1);
}
signed main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> m;
cnt = n;
num = 0;
for (rint i = 1; i <= 2 * n; i++)
{
e[i].clear(), g[i].clear();
dfn[i] = low[i] = sz[i] = 0;
}
for (rint i = 1; i <= m; i++)
{
int a, b;
cin >> a >> b;
e[a].push_back(b);
e[b].push_back(a);
}
tarjan(1, 0);
tot = 0;
dfs(1, 0);
int q;
cin >> q;
while (q--)
{
int ans = 0, x, y;
cin >> x >> y;
if (in[x] > in[y]) swap(x, y);
if (in[x] <= in[y] && out[x] >= out[y])
{
int w = get(y, x);
ans = sz[w] - sz[y] + 2;
}
else ans = n - sz[x] - sz[y] + 2;
cout << ans << endl;
}
}
return 0;
}
Pjudge.21795 排序
题解没看懂。选择学习另一种抽象分治做法。
考虑只有 \(0,1\),将连续段放在一起考虑,形如 \(10101010 \cdots\),考虑一次操作让 \(0\) 连续段个数减半,分段类似 \(1|0|10|1|0|10\cdots\),最后可能会搞出 \(101\) 的形式,再来一次操作 \(1|01\),就能排好序了。
考虑分治,将 \(\le n/2\) 的看成 \(0\),\(\gt n/2\) 的看成 \(1\),进行只有 \(0,1\) 的算法,然后往两边递归,同一层可以放在一起处理,如果最后顺序不对再整体 reverse 一下就行。操作次数大概是 \(0.5 \cdot\log^2 n\)
复杂度未知,能过。
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
#define x first
#define y second
using namespace std;
const int N = 2e4 + 5;
vector<vector<int>> s;
vector<int> k;
pair<int, int> p[N];
int n, a[N], d[N];
int cnt;
struct node
{
int l, r, mid;
} b[N], c[N];
void solve(int l, int r, int mid)
{
int tot = 0;
for (rint i = l; i <= r; i++) d[i] = (a[i] > mid);
for (rint i = l; i <= r; i++)
{
if (i == l || d[i] != d[i - 1]) p[++tot] = make_pair((int)i, (int)i);
else p[tot].y++;
}
if (tot == 1 || (tot == 2 && !d[p[1].x]))
{
k.push_back(r - l + 1);
return;
}
if (tot == 3 && d[p[1].x])
{
k.push_back(p[3].y - p[2].x + 1);
k.push_back(p[1].y - p[1].x + 1);
return;
}
if (!d[p[tot].x])
{
k.push_back(p[tot].y - p[tot].x + 1);
tot--;
}
for (rint i = tot; i >= 1; i -= 6)
{
if (i == 1) k.push_back(p[i].y - p[i].x + 1);
else
{
k.push_back(p[i].y - p[i - 1].x + 1);
if (i >= 3)
{
k.push_back(p[i - 2].y - p[i - 2].x + 1);
if (i == 4) k.push_back(p[i - 3].y - p[i - 3].x + 1);
else if (i >= 5)
{
k.push_back(p[i - 3].y - p[i - 4].x + 1);
if (i >= 6) k.push_back(p[i - 5].y - p[i - 5].x + 1);
}
}
}
}
}
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++) cin >> a[i];
b[++cnt] = (node) {1, n, (n + 1) / 2};
while (1)
{
bool flag = 0;
for (rint i = 1; i <= n - 1; i++) if (a[i] > a[i + 1]) flag = 1;
if (!flag) break;
flag = 0;
while (1)
{
k.clear();
int now = n;
for (rint i = cnt; i >= 1; i--)
{
solve(now - (b[i].r - b[i].l + 1) + 1, now, b[i].mid);
now -= b[i].r - b[i].l + 1;
}
if (!flag && (int)k.size() == cnt) break;
reverse(k.begin(), k.end());
if (k.size() > 1) s.push_back(k);
for (rint i = 1; i <= n; i++) d[i] = a[i];
int now_ = 0;
for (rint i = k.size() - 1; i >= 0; i--)
{
for (rint j = 1; j <= k[i]; j++) a[now_ + j] = d[n - now_ - k[i] + j];
now_ += k[i];
}
reverse(b + 1, b + cnt + 1);
flag ^= 1;
}
int idx = 0;
for (rint i = 1; i <= cnt; i++)
{
if (b[i].l == b[i].r) c[++idx] = b[i];
else
{
c[++idx] = (node){b[i].l, b[i].mid, (b[i].l + b[i].mid) / 2};
c[++idx] = (node){b[i].mid + 1, b[i].r, (b[i].mid + 1 + b[i].r) / 2};
}
}
cnt = idx;
for (rint i = 1; i <= cnt; i++) b[i] = c[i];
}
cout << s.size() << endl;
for (rint i = 0; i <= (int)s.size() - 1; i++)
{
cout << s[i].size() << " ";
for (rint j = 0; j <= (int)s[i].size() - 1; j++) cout << s[i][j] << " ";
cout << endl;
}
return 0;
}
Pjudge21739. 青鱼和序列
非常好贪心 + 数学题
首先考虑对于这两个操作干什么的要搞明白。
对于一个回文串,执行操作一操作二没有区别。而操作二可以使串变成回文串。
非常好性质,所以只要执行了操作二剩下的操作意义就一样了。枚举每一个位置对其执行操作二剩下的执行操作一就可以了。最后在所有答案里取最优的。
算法可以继续优化,序列不一样不代表答案不一样。发现只要执行了操作二,无论操作二在哪里执行对答案都不会产生影响。所以我们只需要在全部执行操作一和执行一次操作一剩下的全部执行操作二中取优的即可。
怎么推这个式子呢?对于原序列不进行操作,答案为:
对其执行一次操作一:
我们设 \(s\) 为上边第一个式子,\(s2\) 为 \(n\) 倍的前缀和。
数形结合一下,大概就是这么一个图。
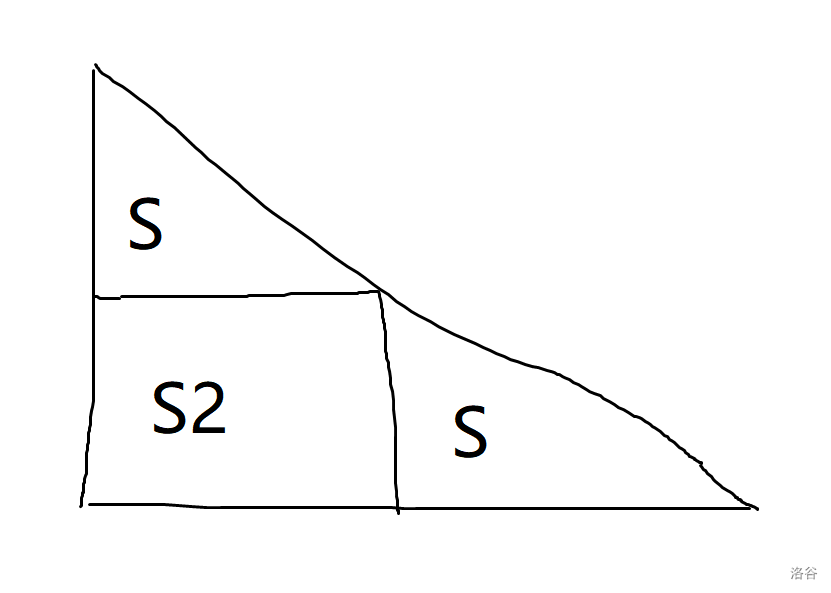
然后一直往下画,每次层数翻倍。那么可以得出进行 \(i\) 次操作一答案,至于如果有操作二,就是右边斜着的三角形一半是 \(s\) 一半是 \(s3\) 即可。\(s3\) 表示倒过来,即 \(a_1+2a_2+...+na_n\)
最后直接算就可以了。
复杂度 \(O(n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int mod = 1e9 + 7;
int n, m;
int s, s2, s3;
int qpow(int a, int b)
{
if (b <= 0) return 1;
int res = 1;
while (b)
{
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res % mod;
}
signed main()
{
cin >> n >> m;
for (rint i = 1; i <= n; i++)
{
int x;
cin >> x;
s = (s + ((n - i + 1) * x % mod)) % mod;
s2 = (s2 + (n * x % mod)) % mod;
s3 = (s3 + (i * x % mod)) % mod;
}
int p1 = qpow(2, m - 1), p2 = p1 * 2 % mod;
int ans1 = (((p2 - 1) * p1) % mod * s2) % mod;//矩形和
int ans2 = p1 * (s3 + s) % mod; //执行了一次操作二一半正三角一半倒三角
int ans3 = s * p2 % mod;
cout << max((ans1 + ans2) % mod, (ans1 + ans3) % mod) << endl;
return 0;
}
Pjudge21743. 青鱼和怪兽
假设没有这个复活操作。可以直接 dp
设 \(f_{i,j}\) 表示玩家有 \(i\) 滴血, 怪兽有 \(j\) 滴血的答案,那么有
但是现在复活操作了。对于这种我们可以使用二分答案二分最终答案再回去 dp 看看合不合法。但是二分的前提是有单调性。
设 \(x=f_{n,m}\),那么 \(f_{i,j}\) 就变成了一个关于 \(x\) 的函数,求导,其值域 \([0,1]\) ,那么有 \(f_{n,m}-x\) 是一个单减函数
二分 \(x\),如果 \(f_{n,m} > x\),那么 \(ans>x\) 反之亦然
复杂度 \(O(k \log n)\),至于 \(k\) 是多少,取决于实数域上二分的次数,看心情,稍微大一一点能过就可以。
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e3 + 5;
int n, m, c;
double p;
double f[N][N];
bool check(double x)
{
for (rint i = 1; i <= n; i++) f[i][0] = 0;
for (rint i = 1; i <= m; i++) f[0][i] = x;
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= m; j++)
f[i][j] = min(x, f[i][j - 1] * p + f[i - 1][j] * (1 - p) + 1);
return x > f[n][m];
}
signed main()
{
cin >> n >> m >> c;
p = c / 100.;
double l = 0, r = 1e18;
int times = 100;
while (times--)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
cout << fixed << setprecision(20) << min(l, 1e9) << endl;
return 0;
}
Pjudge21741. 青鱼和区间
设 \(S_i\) 为覆盖 \(i\) 的线段的集合,那么题目的条件就是让 \(S_i\) 互不相等。
互不相等很不好求,考虑容斥,那么就是考虑将总方案数减去有一些
\(S_i\) 相等的情况。
设 \(c_i\) 表示从一段区间中任意选取若干线段的方案数,由于线段有两个端点,而有 \(i+1\) 个点,那么 \(c_i=2^\binom{i+1}{2}\)。对于划出一个长度为 \(j\) 的区间,内部的方案数为 \(c_{j-2}\)
设 \(f_i\) 为 \(i\) 个数使得两两 \(S_i\) 不相等的方案数,\(g_{i,j}\) 表示将 \(i\) 个数划分成 \(j\) 段的方案数。有
dp 求解即可,复杂度 \(O(n^3)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 3e2 + 5;
const int M = 1e5 + 5;
int n, P;
int f[N], g[N][N];
int pw[M];
int c(int n) {return pw[n * (n + 1) / 2];}
signed main()
{
cin >> n >> P;
g[0][0] = pw[0] = 1;
for (rint i = 1; i <= n * n; i++) pw[i] = 2 * pw[i - 1] % P;
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= i; j++)
for (rint k = 1; k <= i; k++)
g[i][j] = (g[i][j] + g[i - k][j - 1] * c(k - 2)) % P;
f[i] = c(i);
for (rint j = 1; j < i; j++) f[i] = (f[i] - g[i][j] * f[j] % P + P) % P;
}
cout << f[n] << endl;
return 0;
}
Pjudge.21703 治病
假如没有庸医,将所有答案算出来。经典区间问题,开个 vector 记录端点扫一下即可。
一定存在一些情况,算上庸医或者不算上庸医答案一样,如果庸医的药方已经被覆盖了,那么就是原答案。如果没有被覆盖,算出来区间区间答案即可。
复杂度 \(O(K \log K)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 5e5 + 5;
int n, m;
int c[N], ans[N], res;
vector<pair<int, int>> v[N];
signed main()
{
cin >> n >> m;
for (rint i = 1; i <= m; i++) cin >> c[i];
for (rint i = 1; i <= n; i++)
{
int l, r, k, x;
cin >> l >> r >> k;
while (k--)
{
cin >> x;
v[x].push_back({l, i});
v[x].push_back({r + 1, -i});
}
}
for (rint i = 1; i <= m; i++)
{
sort(v[i].begin(), v[i].end());
set<int> s;
int l = 0;
for (auto y : v[i])
{
int r = y.first, p = y.second;
if (s.size()) res += c[i] * (r - l);
if (s.size() == 1) ans[*s.begin()] += c[i] * (r - l);//只被覆盖一次的位置
if (p > 0) s.insert(p);
else s.erase(-p);
l = r;
}
}
for (rint i = 1; i <= n; ++i) cout << res - ans[i] << " ";
return 0;
}
Pjudge21704. 拓扑序计数
观察数据范围,发现 \(n≤20\),显然状压 dp
设 \(f(S)\) 表示按照拓扑序从前往后的顺序往空集加点,到已经加入 \(S\) 这个点集,这一段的加点方案数。设 \(g(S)\) 表示按照拓扑序从后往前的顺序删点,初始为全集,到现在还剩下 \(S\) 这个点集,此时删除顺序的方案数。
对于 \(i,j\) 的答案为 \(\sum_{i\in S,j\notin S}f(S)g(S\cup \{j\})\)
复杂度 \(O(n^22^n)\)
可以继续优化,枚举 \(S,j\),相当于 \(\forall i\in S\),\(ans_{i,j}\) 都加上一个定值。因此瓶颈在于求所有 \(\sum_{i\in S}a_S\)。可以用下面的方法:
for i from n-1 downto 0:
for j from 2^i to (2^{i+1}-1):
ans[i]+=dp[j]
dp[j-2^i]+=dp[j]
dp[]用来辅助转移
复杂度 \(O(n2^n)\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
#define m(a) memset(a, 0, sizeof a)
using namespace std;
const int N = 2e6 + 5;
int n, m;
int a[N], b[N];
int f[N], g[N], dp[N];
int ans[N];
signed main()
{
int T;
cin >> T;
while (T--)
{
cin >> n >> m;
m(a), m(b), m(f), m(g);
f[0] = g[0] = 1;
for (rint i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
u--, v--;
a[v] |= (1 << u);
b[u] |= (1 << v);
}
for (rint i = 0; i < (1 << n); i++)
{
for (rint j = 0; j < n; j++)
{
if (!((i >> j) & 1))
{
if ((i | a[j]) == i) f[i | (1 << j)] += f[i];
if ((i | b[j]) == i) g[i | (1 << j)] += g[i];
}
}
}
for (rint i = 0; i < n; i++)
{
m(ans);
for (rint j = 0; j < (1 << n); j++)
{
dp[j] = 0;
if (!((j >> i) & 1) && (j | a[i]) == j)
dp[j] += f[j] * g[((1 << n) - 1) ^ j ^ (1 << i)];
}
for (rint j = (1 << n) - 1; j > 0; j--)
{
int p = __builtin_ctz(j);
ans[p] += dp[j];
dp[j ^ (1 << p)] += dp[j];
}
for (rint j = 0; j < n; j++) cout << ans[j] << " ";
cout << endl;
}
}
return 0;
}
P11206 「Cfz Round 9」Dove
显然结论题,没打这场比赛。hanss6 那个人机打了然后和 htdlz 赛时口糊了逆天做法,还有十分钟结束比赛,我在旁边,也看了一眼。一眼秒了,但是这群人机一直坚守他们的抽象排序做法,难评。
显然的,为了让赋值满足条件,一定是一大一小这样排。度数大的点影响大,所以让度数大的点小一点度数小的点大一点。(所以 htdlz 直接按照度数排序给点)这样肯定不行,只是一个思考过程不代表如此构造。但这个点提醒我们 \(n\) 一定在叶子节点。所以 dfs 一遍,令 \(l = 1,r=n\),\(x\) 节点为 \(r\),\(father\) 节点为 \(l\),然后\(r--,l++\)
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 5;
const int M = N << 2;
int n;
int l, r, num[N];
int h[N], e[M], ne[M], idx;
void add(int a, int b)
{
e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}
void dfs(int x, int father)
{
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
if (y == father) continue;
dfs(y, x);
}
if (!num[x])
{
num[x] = r--;
if (father && !num[father]) num[father] = l++;
}
}
signed main()
{
int T;
cin >> T;
while (T--)
{
cin >> n; idx = 0;
memset(num, 0, sizeof num);
memset(h, 0, sizeof h);
for (rint i = 1; i < n; i++)
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
l = 1, r = n;
dfs(1, 0);
for (rint i = 1; i <= n; i++) cout << num[i] << " ";
cout << endl;
}
return 0;
}
P11207 「Cfz Round 9」Rose
这个题的策略实在是太长了所以我们直接复制题解
显然的,我们不管原序列是什么直接去构造序列,最多操作次数不会超过 \(2\) 次,因为只需要让她的第一第二和我的第一字母不一样即可。然后分讨即可。瓶颈在于 check 是 \(n^2\) 的
懒得写复制题解算了
自然的想法是,先判一下是否不用操作就能使她获胜,判断方式是直接模拟打出卡牌的过程,时间复杂度为 \(O(n)\)。如果不操作的情况下她无法获胜,再进行接下来的操作,此时答案至少为 1。
我们从特殊性质下手。
考虑 \(s_1 \neq t_1\) 的时候。此时只需要将 \(s_2\) 修改为既不等于 \(s_1\) 又不等于 \(t_1\) 的卡牌即可使她获胜。答案为 1。下面讨论的全是 \(s_1 = t_1\) 的情况。
考虑 \(s_1 \neq s_2\) 的情况,只需要修改 \(t_1\) 为既不等于 \(s_1\) 又不等于 \(s_2\) 的卡牌即可使她获胜。答案为 1。
考虑 \(s_1=s_2=t_1\) 的情况,只需要将 \(s_2,t_1\) 修改使得 \(s_1,s_2,t_1\) 都不相等即可使她获胜。因此最终答案不超过 2。
此时我们可以得到一个 \(O(n^2)\) 的想法。枚举每一个 \(s_i\) 和 \(t_i\),考虑将其修改为其它颜色的卡牌是否能够使她获胜,每次判断的时间复杂度都为 \(O(n^2)\)。如果没有办法只修改一个位置就使她获胜,则答案为 2。
我们考虑如何删去这个判断的 \(O(n)\)。我们从前往后枚举可修改位置。记数组 \(can_{i,j}\) 表示可以将字符 \(i\) 变为字符 \(j\),\(cnt_i\) 表示字符 \(i\) 出现的次数。我们注意到,若到了她打出卡牌,且此时打出卡牌数为 3 的倍数的时候,\(cnt\) 里的最大值减去最小值恰好为 2,且对应最大值的字符 \(p\) 可以变为对应最小值的字符 \(q\),那么仅需要在这次打出卡牌及之前,将一个 \(p\) 修改为 \(q\) 即可使得她获胜,答案为 1。考虑证明:到她打出卡牌的时候,\(cnt\) 之和为奇数且为 3 的倍数,因此若 \(cnt\) 里的最大值减去最小值恰好为 2,则 \(cnt\) 里的数必然可以被表示成 \(\{x,x+1,x+2\}\),将 \(p\) 修改为 \(q\) 后,\(cnt\) 即变为 \(\{x,x,x\}\),满足条件。
接下来的问题是,如何判断字符 \(p\) 是否可以被修改为 \(q\)。对于你的打出卡牌,若你某次打出卡牌后获胜,则这次打出卡牌后的所有卡牌修改都是无用的,因为如果不在这次打出卡牌前修改的话,你必然获胜。这里可以记一个 \(flag=0/1\) 表示是否可以修改。对于 \(flag=1\) 时,所有出现过的 \(s_i\) 和 \(t_i\) 都可以被任意修改,也即 \(can_{s_i,P/V/W}=1,can_{t_i,P/V/W}=1\)。但同时还要注意到,若到了你打出卡牌且打出卡牌数为 3 的倍数时,我们也要进行一次判断。若\(cnt\) 里的最大值减去最小值恰好为 2,且对应最大值的字符 \(p\) 可以变为对应最小值的字符 \(q\),则 \(can_{p,q}=0\)。因为如果在这之前把 \(p\) 变为了 \(q\),则你会在这一局获胜。
如果做完了上面的判断后她都无法获胜,则答案为 2。
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5 + 5;
int n;
char s[N], t[N];
int to[N];
bool check()
{
int cnt[4] = {0};
for (rint i = 1; i <= n; i++)
{
cnt[to[s[i]]]++;
if (cnt[0] == cnt[1] && cnt[1] == cnt[2]) return 1;
cnt[to[t[i]]]++;
if (cnt[0] == cnt[1] && cnt[1] == cnt[2]) return 0;
}
return 0;
}
void solve()
{
cin >> n;
cin >> (s + 1) >> (t + 1);
if (check())
{
puts("0");
return;
}
if (s[1] != t[1])
{
if (s[1] != s[2] && t[1] != s[2]) puts("0");
else puts("1");
return;
}
if (s[1] != s[2])
{
puts("1");
return;
}
int cnt[4] = {0};
bool can[4][4] = {0};
bool flag = 0;
for (rint i = 1; i <= n; i++)
{
cnt[to[s[i]]]++;
if (!flag) for (rint j = 0; j < 3; j++) can[to[s[i]]][j] = 1;
if (i % 3 == 2)
{
int p = 0, q = 0;
if (cnt[1] > cnt[p]) p = 1;
if (cnt[2] > cnt[p]) p = 2;
if (cnt[1] < cnt[q]) q = 1;
if (cnt[2] < cnt[q]) q = 2;
if (cnt[p] - cnt[q] == 2 && can[p][q])
{
puts("1");
return;
}
}
cnt[to[t[i]]]++;
if (!flag) for (rint j = 0; j < 3; j++) can[to[t[i]]][j] = 1;
if (i % 3 == 0)
{
if (cnt[0] == cnt[1] && cnt[1] == cnt[2]) flag = 1;
int p = 0, q = 0;
if (cnt[1] > cnt[p]) p = 1;
if (cnt[2] > cnt[p]) p = 2;
if (cnt[1] < cnt[q]) q = 1;
if (cnt[2] < cnt[q]) q = 2;
if (cnt[p] - cnt[q] == 2) can[p][q] = 0;
}
}
puts("2");
}
signed main()
{
to['P'] = 0, to['V'] = 1, to['W'] = 2;
int T;
cin >> T;
while (T--) solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号