2024.10.16 模拟赛

2024.10.16 模拟赛

T1 divide

简要题意

给定一棵树的 $n$ 个结点以及每个结点的 $fa_i$，每个点的点权 $v_i$，删除树中的两条边，将树拆分为三个非空部分。每个部分的权值等于该部分包含的所有节点的权值之和。出一种合理的拆分方案。根节点的 $fa_i = 0$

$n≤10^6$

solution

首先可以算出所有的点的点权和，如果不是 $3$ 的倍数，那么一定不存在合法的方案。

令 $g=\sum v_i/3$。也就是说，我们只需要求出每个树的子树大小就行了。其实这个过程直接循环扫一遍就行。但是，由于要拆分，直接循环扫无法实现拆下去使子树大小减小的过程（实测得分为 45pts），所以直接 dfs，$sum[i]$ 记录子树点权和。如果 $sum[i]=g$ 就记录答案，并且切去当前子树令 $sum[i]=0$。最后合法位置超过三个则存在方案。否则输出 $-1$

#include <bits/stdc++.h>

#define rint register int
#define int long long
#define endl '\n'

using namespace std;

const int N = 2e6 + 5;
const int M = N << 1;

int n;
int fa[N], v[N];
int h[N], e[M], ne[M], idx;
int sum[N];
int ans[N];
int top;
int goal;

void add(int a, int b)
{
	e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}

void dfs(int x)
{
	for (rint i = h[x]; i; i = ne[i])
	{
		int y = e[i];
		dfs(y);
		sum[x] += sum[y];
	}
	if (goal == sum[x]) 
	{
		ans[++top] = x;
		sum[x] = 0;
	}
}

signed main()
{
	cin >> n;
	int res = 0, root = 0;
	for (rint i = 1; i <= n; i++) 
    {
		cin >> fa[i] >> v[i];
		res += v[i];
		sum[i] = v[i];
		if (fa[i] == 0) root = i;
		else add(fa[i], i);
	}
	if (res % 3)
	{
		cout << -1 << endl;
		return 0;
	}
	goal = res / 3;
	dfs(root);
	if (top > 2) cout << ans[1] << " " << ans[2];
	else cout << -1 << endl;
    return 0;
}

T2 color

题目大意

给定一个 $n$ 个结点的树，每个节点都有颜色为黑或白，从黑色节点无法到达白色节点，反之亦然。每次染色操作可以选择一个节点 $v$，并改变节点 $v$ 以及其所有可达同色节点的颜色。希望将树中的所有节点都染成同一种颜色，求最少操作次数。

$n≤2 \times 10^5$

solution

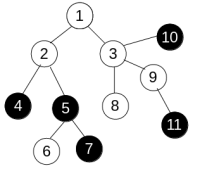
神仙题

放个样例，第一眼看过去，我的想法是维护类联通块的东西。如 $2,1,3,8,9$ 为一个联通块。最后数黑色和白色联通块个数取 $min$。

结果大样例过不去。

很简单就能 hack 掉，给一个一直黑白交错的非常长单链，随便接一个特别短的黑白交错的支链，上面那种做法就不行了。因为答案会比正解小。

那怎么做呢？

从特殊到一般，假设这是一条链。那么答案就是设黑白交替的次数为 $cnt$，答案为 $⌊\frac{cnt}{2}⌋$。那么对于一棵树，其实就是在这条链上加一些分支。

那么，如果我这条链，为黑白交替次数最多的一条链，对于这棵树的答案就等于对于这条链的答案。因为操作这条链的时候，其他链条的染色也一定会随着这条链的染色而颜色统一。原因为支链的黑白交错次数少并且染色操作为联通着就能染色。

所以，只需要类比求树的直径来求这条黑白交错次数最多的链条即可。这里使用两次 dfs，代码容易实现。先求出对于 $x$ 黑白交错次数最多的链条远处端点为 $y$，再求出对于 $y$ 的最远端点 $z$，那么 $y->z$ 即为所求，然后求出 $cnt$，即可求出答案。

复杂度 $O(n)$

#include <bits/stdc++.h>

#define rint register int
#define int long long
#define endl '\n'

using namespace std;

const int N = 2e5 + 5;
const int M = 4e5 + 5;

int n;
int a[N];
int h[N], e[M], ne[M], idx;
int dist, ed;

void add(int a, int b) 
{
	e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}

void dfs(int x, int father, int w)
{
	if (w > dist)
	{
		dist = w;
		ed = x;
	}
	for (rint i = h[x]; i; i = ne[i])
	{
		int y = e[i];
		if (y == father) continue;
		dfs(y, x, w + (a[x] != a[y]));
	}
}

signed main() 
{
	cin >> n;
	for (rint i = 1; i <= n; i++) cin >> a[i];
	for (rint i = 1; i < n; i++)
    {
		int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs(1, 0, 0);
	dist = 0;
	dfs(ed, 0, 0);
	cout << (dist + 1) / 2 << endl;
	return 0;
}

T3 count

简要题意

对于一个长度为 $n$ 的小数（包括小数点）执行最多 $k$ 次四舍五入，四舍五入最多执行到小数点处，不于整数位进行四舍五入。求最后答案的最大值。

$n≤2 \times 10^5,k≤10^9$

solution

这个题卡了很久，因为卡在执行四舍五入操作上了。因为我在担心当前四舍五入是否优秀，后来才发现，我所担心的，类似于把 $3.98$ 四舍五入成 $4.08$.........（$8$ 先不动跳过去，然后四舍五入 $3.9$）

$k$ 根本不用管它，复杂度瓶颈与它无关，它的上限不会影响操作的执行，但是下限会。

执行过程为，找到第一个大于等于 $5$ 的位置执行四舍五入，此时一定是最优的，从此处开始四舍五入即可。每四舍五入一次 $k--$，如果最后结束操作时如果 $k<1$ 就说明整数位也进行了一次四舍五入，输出的时候开头加个 $1$ 即可。

#include <bits/stdc++.h>

#define rint register int
#define int long long
#define endl '\n'

using namespace std;

int n, m;
string s;

signed main()
{
    cin >> n >> m; cin >> s;
    int pos = s.find('.');
    int k = pos + 1;
    while (k < s.size() && s[k] < '5') k++;
    if (k == s.size()) 
	{
		cout << s << endl;
		return 0;
	}
    s = s.substr(0, k); //后边一定会被四舍五入成 0
    k--, m--; //进了一次位
    while (k >= 0)
    {
        if (s[k] != '.')
        {
        	s[k]++;
            if (s[k] < '5') break; //进位进不动了
            if (s[k] <= '9')
            {
                if (!m || k < pos) break;
                s[k] = '0';
                m--;
            }
            else s[k] = '0';
        }
        k--;
    }
    if (k < 0) s = "1" + s;
    while (s.back() == '0') s.pop_back();
    if (s.back() == '.') s.pop_back();
    cout << s << endl;
    return 0;
}

T4 change

简要题意

给定一个长度为 $n$ 的非负整数序列 $a_1,a_2,…,a_n$。其中的所有元素将被逐个封印。具体封印顺序可以用一个 $1$∼$n$ 的排 $b_1,b_2,…,b_n$ 来描述，第 $i$ 个被封印的元素即为 $a_{b_i}$

完成 $n$ 个任务，第 $i$ 个任务是：对于完成前 $i$ 次封印的序列，请你找到序列中的一个连续子序列（可以为空），使得该子序列不含任何被封印的元素，且子序列内各元素之和尽可能大，输出这个子序列元素和的最大可能值。空序列元素和为 $0$。

$n≤10^5$

solution

正解是并查集进行贪心

但是我们可以进行一个投机取巧

这个题其实就是在求最大子序列和，但是中间有些位置不能选。那么我们将不能选的位置设置成无穷小就行了。这样就就算选了这个位置，也不会改变最终答案，因为选了它也不是最大的，这样就可以正常使用线段树进行维护了。

剩下的就是板子了

#include <bits/stdc++.h>

#define rint register int
#define int long long
#define endl '\n'

#define ls p << 1
#define rs p << 1 | 1

using namespace std;

const int N = 1e5 + 5;
const int M = 2e6 + 5;

int n, m;
int w[N];
struct node 
{
	int l, r;
	int tmax, lmax, rmax, sum;
} t[M];

void push_up(node &p, node &l, node &r) 
{
	p.sum = l.sum + r.sum;
	p.lmax = max(l.lmax, l.sum + r.lmax);
	p.rmax = max(r.rmax, r.sum + l.rmax);
	p.tmax = max({l.rmax + r.lmax, l.tmax, r.tmax});
}

void push_up(int p) 
{
	push_up(t[p], t[ls], t[rs]);
}

void build(int p, int l, int r) 
{
	if (l == r) 
	{
		t[p] = {l, r, w[r], w[r], w[r], w[r]};
		return ;
	}
	t[p] = {l, r, 0, 0, 0, 0};
	int mid = (l + r) >> 1;
	build(ls, l, mid);
	build(rs, mid + 1, r);
	push_up(p);
}

void change(int p, int x, int v) 
{
	if (t[p].l == x && t[p].r == x) 
	{
		t[p] = {x, x, v, v, v, v};
		return ;
	}
	int mid = (t[p].l + t[p].r) >> 1;
	if (x <= mid) change(ls, x, v);
	else change(rs, x, v);
	push_up(p);
}

node query(int p, int l, int r) 
{
	if (t[p].l >= l && t[p].r <= r) return t[p];
	int mid = (t[p].l + t[p].r) >> 1;
	if (r <= mid) return query(ls, l, r);
	else if (l > mid) return query(rs, l, r);
	else 
	{
		node left = query(ls, l, r);
		node right = query(rs, l, r);
		node res;
		push_up(res, left, right);
		return res;
	}
}

signed main() 
{
	cin >> n;
	for (rint i = 1; i <= n; i++) cin >> w[i];
	build(1, 1, n);
	m = n;
	while (m--) 
	{
		int y;
		cin >> y;
		change(1, y, -1e14);
		cout << max(0ll, query(1, 1, n).tmax) << endl;
	}
	return 0;
}