2024.5.18 杂题
2024.5.18 杂题
「SMOI-R1」Apple
两个操作，修改元素，求子集和。
高位前缀和不会。考虑朴素 dp 转移
设 \(f[i]\) 表示二进制下长度为 \(n\) 的数前 \(i\) 位为 \(1\)，后边为 \(0\) 的子集和。理论来说可以转移，但是比较麻烦，考虑优化状态，\(f[i][j]\) 表示前 \(\frac{n}{2}\) 位为 \(i\) 后 \(\frac{n}{2}\) 位为 \(j\) 的子集和。在插入一个 \(a_i\) 时，枚举前 \(\frac{n}{2}\) 位的超集 \(X\)，令 \(f[X][y] += a_i\) ，删除时减去即可。
在查询 \(i\) 的子集和时，枚举后 \(\frac{n}{2}\) 的子集 \(Y\)，答案 \(\sum_{Y \subseteq y} f[x][Y]\)
这些操作与树状数组很类似，仿照树状数组写一个数据结构优化掉，复杂度大概是 \(O(Q \sqrt{N})\)。
const int N = (1 << 20) + 10;
const int M = (1 << 10) - 1;
int n, q;
int a[N];
struct Tree
{
int c[M + 2][M + 2];
void add(int x, int y)
{
int X = x >> 10, Y = x & M;
if (n <= 10) {c[0][Y] += y; return ;}
for (rint i = X; i <= M; i = (i + 1) | X)
c[i][Y] += y;
}
int query(int x)
{
int X = x >> 10, Y = x & M, ans = 0;
for (rint i = Y;; i = (i - 1) & Y)
{
ans += c[X][i];
if (!i) break;
}
return ans;
}
void clear(int x, int y)
{
int X = x >> 10, Y = x & M;
if (n <= 10) {c[0][Y] -= y; return ;}
for (rint i = X; i <= M; i = (i + 1) | X)
c[i][Y] -= y;
}
} tree;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> q;
for (rint i = 0; i < (1 << n); i++)
{
cin >> a[i];
tree.add(i, a[i]);
}
while (q--)
{
int op, x;
cin >> op >> x;
if (op == 1)
{
cout << tree.query(x) << endl;
}
else
{
int y;
cin >> y;
tree.clear(x, a[x]);
a[x] = y;
tree.add(x, a[x]);
}
}
return 0;
}
『STA - R5』RDG
不会博弈论，考虑 dp
设 \(f_{i,j}\) 表示考虑从 \(a_i\) 到 \(a_n\) 这一段，前面进行了 \(j\) 次 \(1\) 操作的情况下先手能不能赢。\(a\) 需要从小到大排序。
\[f_{i,j}=\begin{cases}1&j>a_i\\f_{i+1,j}&j=a_i\\\neg f_{i+1,j}\operatorname{or}\neg f_{i,j+1} &j<a_i\\\end{cases}
\]
当 \(j\le a_i-2\) 时为 \(01\) 相间。所以保留 \(O(1)\) 状态即可通过本题。
bool c(int i, int j)
{
if (i == n || j > a[i]) return 1;
if (j < a[i] - 3) j += (a[i] - 2 - j) / 2 * 2;
if (!v[i][a[i] - j])
{
v[i][a[i] - j] = 1;
if (a[i] == j) f[i][a[i] - j] = c(i + 1, j);
else f[i][a[i] - j] = !(c(i + 1, j) & c(i, j + 1));
}
return f[i][a[i] - j];
}
signed main()
{
int T;
cin >> T;
while (T--)
{
cin >> n;
for (rint i = 1; i <= n; i++) cin >> a[i];
for (rint i = 1; i <= n; i++)
for (rint j = 0; j <= 3; j++)
f[i][j] = v[i][j] = 0;
sort(a + 1, a + n + 1);
if (c(1, 0)) cout << "Alice" << endl;
else cout << "Bob" << endl;
}
return 0;
}
CF1965E
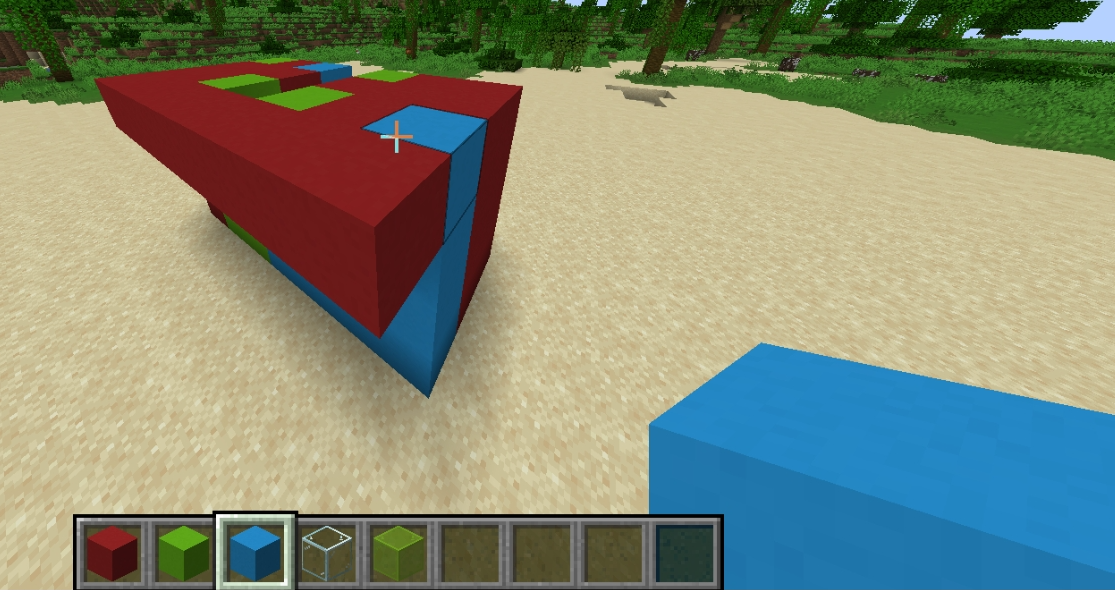
毒瘤构造，虽然尺子姐已经在题解区给出了构造方案，但我还是想自己去搭一搭，于是找 hanss6 要了个 MC。
图中玻璃表示临时空气，混凝土即为不同色方块。
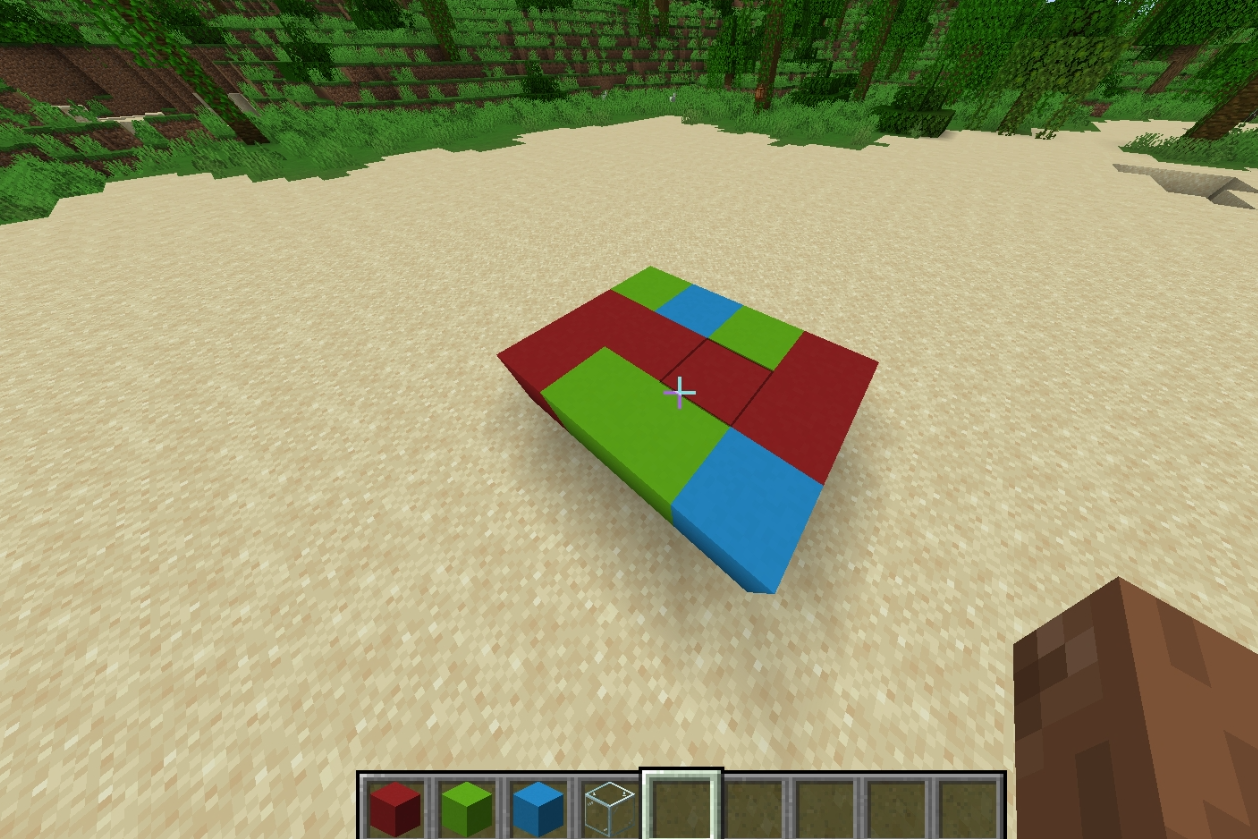
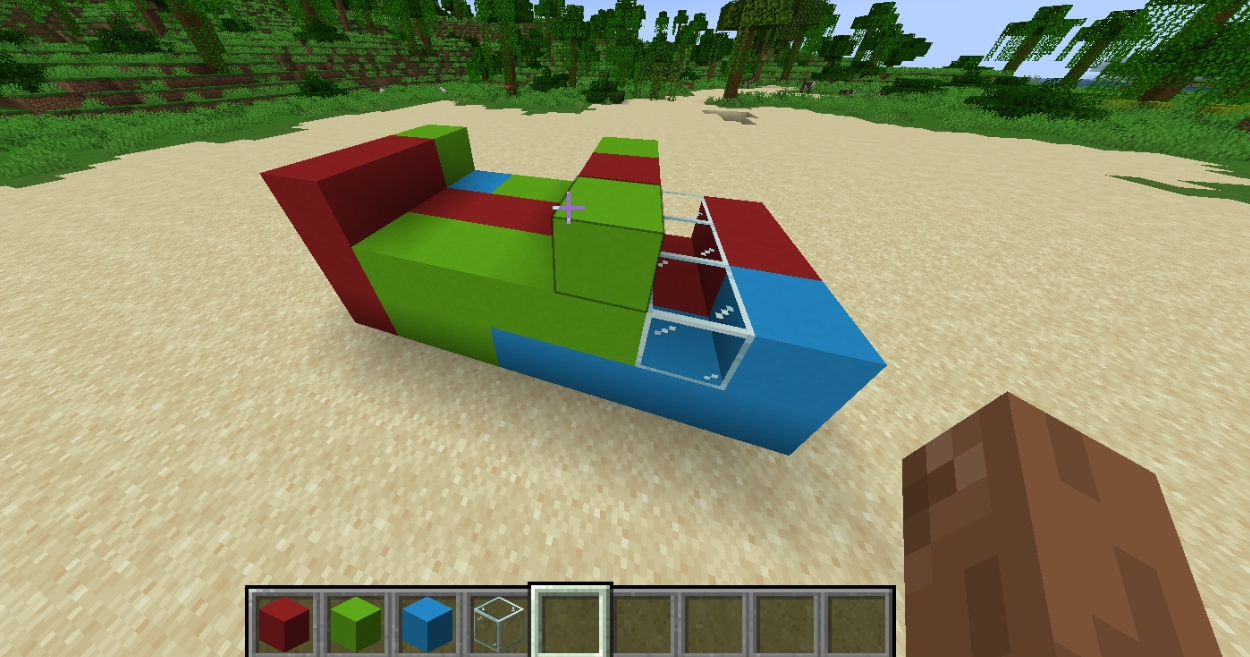
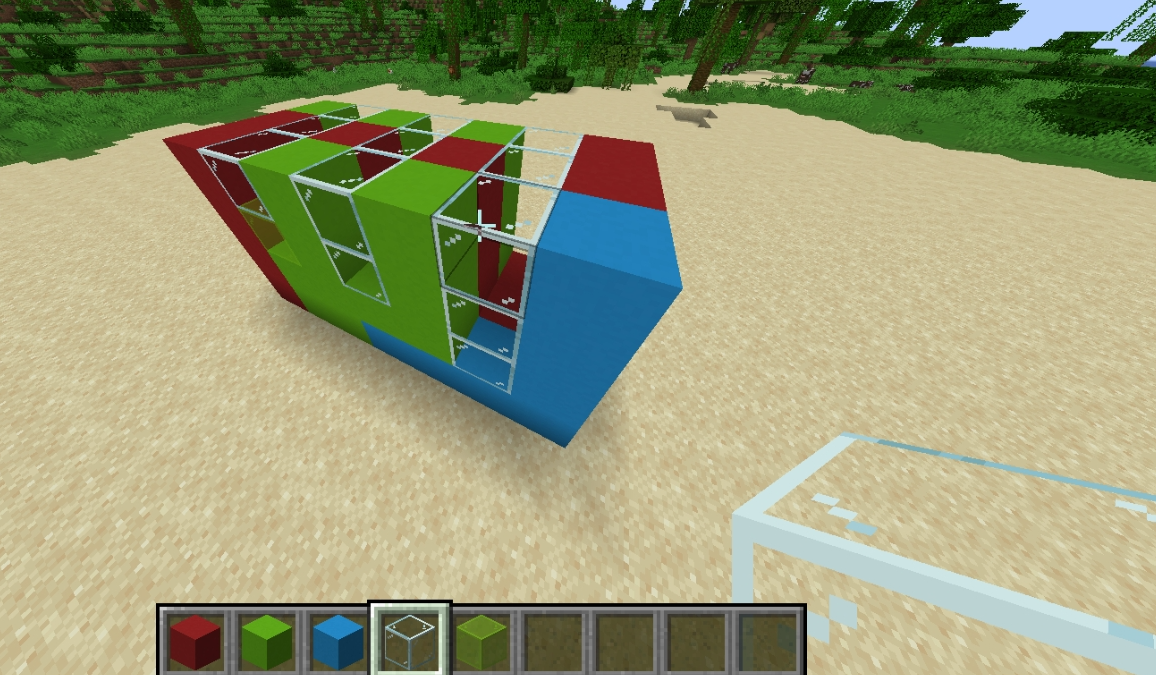
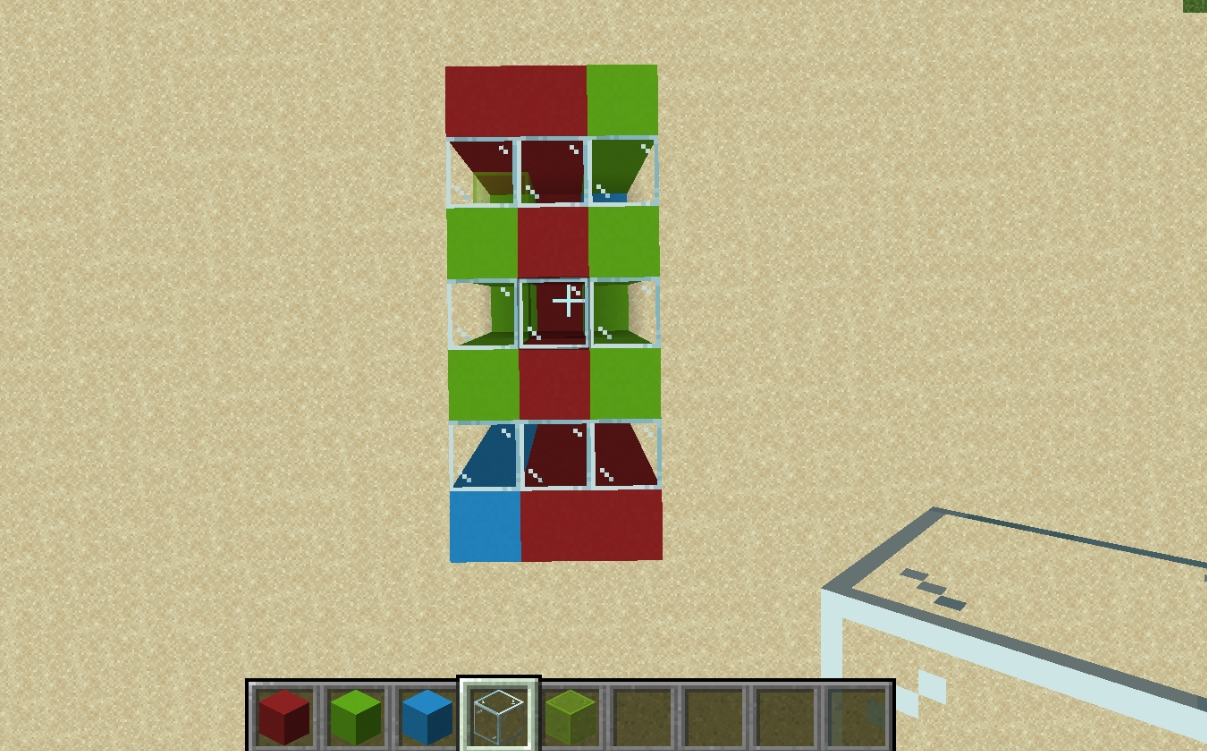
最上层所有混凝土均至少紧挨着一格空气，只需把所有空气替换成一种颜色的混凝土就连通
int n, m, k;
int a[N][N], x[N][N], y[N][N];
vector<tuple<int, int, int, int>> s;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> k;
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= m; j++)
cin >> a[i][j];
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= m; j++)
{
x[i][j] = i;
y[i][j] = j;
}
}
for (rint z = 1; z <= m; z++)
{
if(z >= 2)
{
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= m; j++)
s.ep(x[i][j], y[i][j], z, a[i][j]);
}
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= m; j++)
{
if(j == m - z + 1)
{
for (rint y = j + 1; y <= 2 * j - 1; y++)
s.ep(i, y, z, a[i][j]);
x[i][j] = i;
y[i][j] = 2 * j - 1;
}
}
}
int _m = m;
for (rint p = 1; p <= k; p++)
{
for (rint i = 1; i <= n + 1; i++)
{
for (rint j = 1; j <= 2 * m - 1; j++)
{
if (i == n + 1)
s.ep(i, j, _m, p);
else if (j % 4 == 2 || j >= 2 * m - 3 && !(j % 2))
s.ep(i, j, _m, p);
else if ((j & 1) && _m != m && a[i][(j + 1) / 2] >= p)
s.ep(i, j, _m, a[i][(j + 1) / 2]);
}
}
_m++;
}
cout << s.size() << endl;
for (auto it : s)
{
cout << get<0>(it) << " ";
cout << get<1>(it) << " ";
cout << get<2>(it) << " ";
cout << get<3>(it) << endl;
}
return 0;
}
饥饿的奶牛
考虑直接枚举每一个点。设 \(f[i]\) 为从开始到 \(i\) 时的答案。用 vector 存区间。对于区间 \(a_i\) 有
\[f[s_i.r] = \max_{0≤j≤s_i.l}{\{}f[j]\}
\]
int n;
int f[N];
vector<int> a[N];
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
{
int x, y;
cin >> x >> y;
a[y].push_back(x);
}
for (rint i = 0; i <= M; i++)
{
f[i] = f[i - 1];
int k = a[i].size();
for (rint j = 0; j < k; j++)
{
int val = i - a[i][j] + 1;
if (a[i][j] >= 1) f[i] = max(f[i], f[a[i][j] - 1] + val);
else f[i] = max(f[i], val);
}
}
cout << f[M] << endl;
return 0;
}
[HAOI2006] 数字序列
第一问，考虑不严格上升的序列，则为 \(n-len(LIS)\)，严格上升，则 \(i-j \geq a_i-a_j\)，移项，\(i-a_i \geq j-a_j\)，将 \(a_i\) \(->\) \(a_i-i\) 按照同样方法处理即可。（在代码中对于第一问的 dp 使用 \(g[]\) 表示）
对于第二问，我们设 \(f[i]\) 为开始到 \(i\) 的答案，则
\[f[i]=\max_{g(j)+1=g(i)}\{f(j)+w(j+1,i)\}
\]
对于区间 \([i,j]\) \(\exists k\) 使得 \([i,k]=a_i\), \([k+1,j]=a_j\)，并且 \(\exists k\) 使得其为最优策略，对于每个 \(w\) 暴力 \(k\) 的位置更新答案。
int n, a[N], b[N], len;
int g[N], f[N], c1[N], c2[N];
vector<int> vec[N];
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
{
cin >> a[i];
a[i] -= i;
}
n++;
a[n] = inf;
b[++len] = a[1];
g[1] = 1;
for (rint i = 2; i <= n; i++)
{
if (a[i] >= b[len]) b[++len] = a[i], g[i] = len;
else
{
int pos = upper_bound(b + 1, b + 1 + len, a[i]) - b;
b[pos] = a[i];
g[i] = pos;
}
}
cout << n - len << endl;
a[0] = -inf;
vec[0].push_back(0);
for (rint i = 1; i <= n; i++)
{
f[i] = inf;
for (rint j = 0; j < vec[g[i] - 1].size(); j++)
{
int v = vec[g[i] - 1][j];
if (a[v] > a[i]) continue;
c1[v - 1] = c2[v - 1] = 0;
for (rint k = v; k <= i; k++)
{
c1[k] = abs(a[k] - a[v]);
c2[k] = abs(a[k] - a[i]);
}
for (rint k = v + 1; k <= i; k++)
{
c1[k] += c1[k - 1];
c2[k] += c2[k - 1];
}
for (rint k = v; k <= i; k++)
{
int val = c1[k] - c1[v] + c2[i] - c2[k];
f[i] = min(f[i], f[v] + val);
}
}
vec[g[i]].push_back(i);
}
cout << f[n] << endl;
return 0;
}
SP9941 GRE
设 \(f_i\) 表示以 \(i\) 开头的最长子序列，则 \(f_i=\max\limits_{j\in(i,n]\land \,s_i\text{ ∈}s_j} f_j+w_i\)
用哈希表存每个串 \(s_i\) 及 \(f_i\)。枚举每一个串在他之前所有出现过的串的长度 \(l\)，对于每一个 \(l\) 找出该串所有长度为 \(l\) 的子串，在哈希表里查询即可实现转移。
int T, n;
int ans, v[N], len[N], f[N], s[M];
char c[M];
int *h[N], p[M], tab[M], maxx[M];
int get(int x)
{
int p = x % lim;
while (1)
{
if (tab[p] == -1 || tab[p] == x) break;
p++;
p %= lim;
}
return p;
}
int Hash(int i, int l, int r)
{
return (h[i][r] - h[i][l - 1] * p[r - l + 1] % mod + mod) % mod;
}
signed main()
{
cin >> T;
p[0] = 1;
for (rint i = 1; i < M; i++)
{
p[i] = p[i - 1] * base % mod;
}
int idx = 1;
while (T--)
{
memset(tab, -1, sizeof tab);
memset(maxx, 0, sizeof maxx);
cin >> n;
ans = 0;
for (rint i = 1; i <= n; i++)
{
scanf("%s", c + 1);
cin >> v[i];
len[i] = strlen(c + 1);
f[i] = v[i];
h[i] = (int*)malloc(sizeof(int) * len[i] + 3);
for (rint j = 1; j <= len[i]; j++)
{
h[i][j] = (h[i][j - 1] * base % mod + c[j] - 'a' + 1) % mod;
}
for (rint j = 1; j <= len[i]; j++)
{
if (s[j])
{
for (rint k = 1; k + j - 1 <= len[i]; k++)
{
int x = get(Hash(i, k, k + j - 1));
if (tab[x] != -1) f[i] = max(f[i], maxx[x] + v[i]);
}
}
}
int p = get(Hash(i, 1, len[i]));
tab[p] = Hash(i, 1, len[i]);
maxx[p] = max(maxx[p], f[i]);
ans = max(ans, f[i]);
s[len[i]]++;
}
int max_len = 0;
for (rint i = 1; i <= n; i++)
{
if (i != n) max_len = max(max_len, len[i]);
else
{
for (rint j = 1; j <= max(max_len, len[i]); j++)
s[i] = 0;
}
}
printf("Case #%lld: %lld\n", idx, ans);
idx++;
}
return 0;
}
P3766 核心密码B
对于 \(a^b\)，对每个 \(b\) 单独算贡献。
如果 \(b \ge 3\)，可以不动脑子的朴素实现。
对于 \(b = 2\)，暴力 \(a \le 10^7\) 时直接暴力处理。把 \(\dfrac {1} {x^2}\) 变为 \(\dfrac{\dfrac{1}{(x-1)x}+\dfrac{1}{x(x+1)}}2\) 取近似值，直接裂项。要求
\(\begin{aligned} \sum_{x=10^7+1}^{\sqrt q_i} \frac{1}{2} (\frac{1}{x-1}-\frac{1}{x+1}) = \frac{1}{10^7}+\frac{1}{10^7+1}-\frac{1}{q_i-1}-\frac{1}{q_i} \end{aligned}\)
void solve(int x)
{
ll cnt = 2, r = qpow(cnt, x);
lb sum = 0;
for (rint i = 1; i <= n; i++)
{
while (r <= q[i].x)
{
lb tmp = 1.0;
tmp /= r;
sum += tmp;
cnt++;
r = qpow(cnt, x);
}
s[q[i].id] += sum;
}
}
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
{
cin >> q[i].x;
q[i].id = i;
}
sort(q + 1, q + n + 1, cmp);
for (rint i = 3; i <= 63; i++) solve(i);
for (rint i = 1; i <= n; i++)
{
if (q[i].x > inf)
{
int x = sqrtl(q[i].x);
lb t1 = 1.0, t2 = 1.0, t3 = 1.0, t4 = 1.0;
t1 /= (lb)(1e7);
t2 /= (lb)(1e7 + 1);
t3 /= (lb)(x);
t4 /= (lb)(x + 1);
t1 = t1 * 1.0 + t2 * 1.0 - t3 * 1.0 - t4 * 1.0;
t1 = t1 * 1.0 / (lb)(2.0);
s[q[i].id] += t1;
q[i].x = inf;
}
}
solve(2);
for (rint i = 1; i <= n; i++)
{
cout << setprecision(15) << fixed << s[i] << endl;
}
return 0;
}
CF149D
定义 \(f_{i,j,0 \ or \ 1 or \ 2,0 \ or \ 1 or \ 2}\) 为区间 \([i,j]\)，\(i\) 不染/染成红色/染成蓝色，\(j\) 同理的方案数。分类讨论直接转移即可。
stack<int> s;
int n;
int f[N][N][3][3], mp[N];
//mp 存储对应的括号位置
char a[N];
void dfs(int l, int r)
{
if (l + 1 == r)
{
f[l][r][0][1] = f[l][r][0][2] = f[l][r][1][0] = f[l][r][2][0] = 1;
return ;
}
if (mp[l] == r)
{
dfs(l + 1, r - 1);
for (rint i = 0; i <= 2; i++)
{
for (rint j = 0; j <= 2; j++)
{
if (i != 1) f[l][r][1][0] += f[l + 1][r - 1][i][j], f[l][r][1][0] %= mod;
if (i != 2) f[l][r][2][0] += f[l + 1][r - 1][i][j], f[l][r][2][0] %= mod;
if (j != 1) f[l][r][0][1] += f[l + 1][r - 1][i][j], f[l][r][0][1] %= mod;
if (j != 2) f[l][r][0][2] += f[l + 1][r - 1][i][j], f[l][r][0][2] %= mod;
}
}
}
else
{
dfs(l, mp[l]);
dfs(mp[l] + 1, r);
for (rint i = 0; i <= 2; i++)
for (rint j = 0; j <= 2; j++)
for (rint k = 0; k <= 2; k++)
for (rint p = 0; p <= 2; p++)
if (!(j && j == k))
{
f[l][r][i][p] += f[l][mp[l]][i][j] * f[mp[l] + 1][r][k][p] % mod;
f[l][r][i][p] %= mod;
}
}
}
signed main()
{
scanf("%s", a + 1);
n = strlen(a + 1);
for (rint i = 1; i <= n; i++)
{
if (a[i] == '(') s.push(i);
else
{
mp[s.top()] = i;
s.pop();
}
}
dfs(1, n);
int ans = 0;
for (rint i = 0; i <= 2; i++)
{
for (rint j = 0; j <= 2; j++)
{
ans += f[1][n][i][j];
ans %= mod;
}
}
cout << ans << endl;
return 0;
}
