浅谈最短路问题
Part1. 前言
本篇文章参考文献:
最短路基本原理在这里不多赘述,SPFA 和 dijkstra 原理没有记录,主要内容为全源最短路和单源最短路的各种应用。
Part2.最短路板子
//dijkstra
int idx, h[N], e[M], w[M], ne[M];
int dist[N];
bool v[N];
priority_queue<pair<int, int> > q;
void add(int a, int b, int c)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}
void dijkstra(int s)
{
memset(dist, 0x3f, sizeof dist);
memset(v, 0, sizeof v);
dist[s] = 0;
q.push(make_pair(0, s));
while (!q.empty())
{
int x = q.top().second;
q.pop();
if(v[x]) continue;
v[x] = 1;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
q.push(make_pair(-dist[y], y));
}
}
}
}
signed main()
{
//输入
dijkstra(s);
for (rint i = 1; i <= n; i++) cout << dist[i] << " ";
return 0;
}
//SPFA
int n, m, s;
int idx;
int h[N], e[M], ne[M], dist[N], w[M];
queue<int> q;
bool v[N];
void add(int a, int b, int c)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}
void SPFA(int s)
{
memset(dist, 0x3f, sizeof dist);
memset(v, 0, sizeof v);
dist[s] = 0;
v[s] = 1;
q.push(s);
while(!q.empty())
{
int x = q.front();
q.pop();
v[x] = 0;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
if (!v[y]) q.push(y), v[y] = 1;
}
}
}
}
signed main()
{
SPFA(s);
return 0;
}
Part3.全源最短路
Floyd
模板题传送门 B3647 【模板】Floyd
全源最短路,顾名思义,就是要求出所有点之间的最短路径。既然要求出所有点复杂度必然不会低。Floyd 是一种类似于 dp 的方法,dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]) 进行转移。即可求出答案。
int n, m;
int dist[N][N];
void floyd()
{
for (rint k = 1; k <= n; k++)
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
signed main()
{
cin >> n >> m;
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= n; j++)
{
if (i == j) dist[i][j] = 0;
else dist[i][j] = inf;
}
}
while (m--)
{
int u, v, w;
cin >> u >> v >> w;
dist[u][v] = min(dist[u][v], w);
dist[v][u] = min(dist[v][u], w);
}
floyd();
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= n; j++) cout << dist[i][j] << " ";
cout << endl;
}
return 0;
}
P2886 [USACO] Cow Relay
这道题本质确实是矩阵乘法,我们可以通过类 floyd 的方法进行解决。
void floyd(int c[][N], int a[][N], int b[][N])
{
static int temp[N][N];
memset(temp, 0x3f, sizeof temp);
for (rint k = 1; k <= n; k++)
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);
}
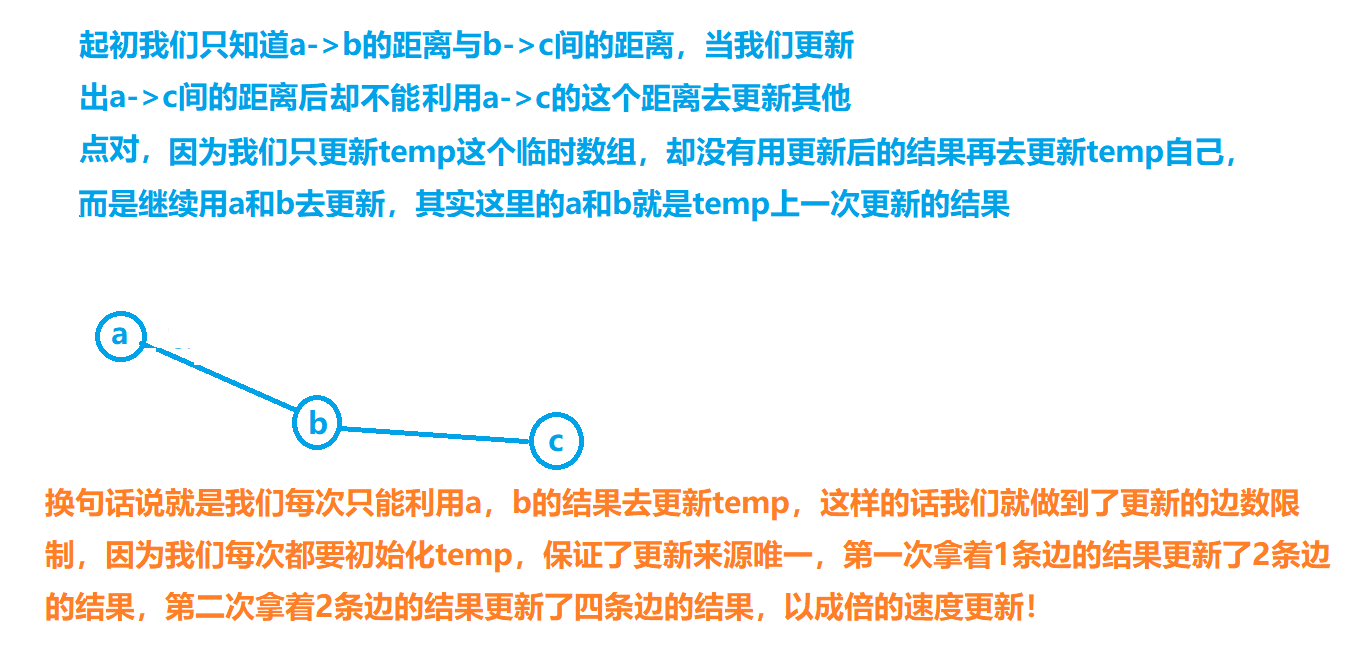
做一次类 Floyd 并不会去用该次的结果自我更新,只会用上一次的结果来更新一次,不像 Floyd 那样可以自己更新自己多次
从 \(Accepting\) 巨佬那里偷一张图:
const int N = 2e2 + 5;
int k, n, m, S, E;
int g[N][N];
int res[N][N];
map<int, int> id;
void floyd(int c[][N], int a[][N], int b[][N])
{
static int temp[N][N];
memset(temp, 0x3f, sizeof temp);
for (rint k = 1; k <= n; k++)
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]);
memcpy(c, temp, sizeof temp);
}
signed main()
{
cin >> k >> m >> S >> E;
memset(g, 0x3f, sizeof g);
//不初始化 g[i][i] = 0
//类 floyd 算法中有严格的边数限制, 如果出现了 i->j->i 的情况其实在 i->i 中是有 2 条边的
//要是我们初始化 g[i][i]=0, 那样就没边了, 影响了类Floyd算法的边数限制
memset(res, 0x3f, sizeof res);
if (!id.count(S)) id[S] = ++n;
if (!id.count(E)) id[E] = ++n;
S = id[S], E = id[E];
while (m -- )
{
int a, b, c;
cin >> c >> a >> b;
if (!id.count(a)) id[a] = ++n;
if (!id.count(b)) id[b] = ++n;
a = id[a];
b = id[b];
g[a][b] = g[b][a] = min(g[a][b], c);
}
for (rint i = 1; i <= n; i++) res[i][i] = 0; //经过0条边
while (k)
{
if (k & 1) floyd(res, res, g);
//res = res * g
//根据 k 决定是否用当前 g 的结果去更新 res
floyd(g, g, g);
//g =g *g
k >>= 1;
}
cout << res[S][E] << endl;
return 0;
}
Johnson
模板题传送门P5905 【模板】全源最短路
\(Dijkstra\) 不能处理负边。但是对于这个题偏偏又有。所以直接跑好几轮 \(Spfa\) ?找死。所以把每条边变成非负值。不能每条边同时加同一个数,这样答案就你不知道最后要减去几个你加的值。
所以,我们先跑一遍 \(Spfa\),顺便记录一些信息,顺手判掉负环。
当我们跑 \(Spfa\) 时,我们可以先设一个虚拟点 \(0\),这个点连上每一个点,边权为 \(0\)。以这个点位源点跑 \(Spfa\),用 \(f\) 数组记录,即 \(0\) 到每个点的最短路,其实这个 f[i] 的作用就是原来的 dist[i]。接着,对于一条边 \(u,v,w_{u,v}\)。由三角形不等式 \(f_u+f_{u,v}≥f_v\) 得,\(w_{u,v}+f_u-f_v≥0\)。只需要将每条边的边权 \(w_{u,v}\) 加上 \((f_u-f_v)\) 即可满足非负。最终求出来的最短路 \(dist_{s,t}\) 减去 \((f_s-f_t)\) 即可。然后在记录答案用一个 vector 即可。
#include <bits/stdc++.h>
#define int long long
#define rint register int
#define endl '\n'
using namespace std;
const int N = 1e5 + 5;
const int M = 1e6 + 5;
const int inf = 1e9;
int n, m;
int idx, h[N], ne[M], e[M], w[M];
int dist[N], cnt[N];
bool v[N];
int f[N];
vector<int> ans;
void add(int a, int b, int c)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}
bool SPFA(int s)
{
queue<int> q;
for (rint i = 1; i <= n; i++) f[i] = inf;
memset(v, 0, sizeof v);
f[s] = 0;
v[s] = true;
q.push(s);
cnt[s] = 0;
while (!q.empty())
{
int x = q.front();
q.pop();
v[x] = 0;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (f[y] > f[x] + z)
{
f[y] = f[x] + z;
cnt[y] = cnt[x] + 1;
if (cnt[y] >= n + 1) return 0;
if (!v[y])
{
q.push(y);
v[y] = 0;
}
}
}
}
return 1;
}
void dijkstra(int s)
{
priority_queue<pair<int, int> > q;
for (rint i = 1; i <= n; i++) dist[i] = inf;
memset(v, 0, sizeof v);
dist[s] = 0;
q.push(make_pair(0, s));
while (!q.empty())
{
int x = q.top().second;
q.pop();
if(v[x]) continue;
v[x] = 1;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
q.push(make_pair(-dist[y], y));
}
}
}
}
void build()
{
cin >> n >> m;
for (rint i = 1; i <= m; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
for (rint i = 1; i <= n; i++) add(0, i, 0);
}
void check()
{
if (!SPFA(0))
{
puts("-1");
exit(0);
}
}
void calc_all_path()
{
for (rint x = 1; x <= n; x++)
{
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
w[i] += f[x] - f[y];
}
}
for (rint i = 1; i <= n; i++)
{
dijkstra(i);
long long res = 0;
for (rint j = 1; j <= n; j++)
{
if (dist[j] == inf) res += j * inf;
else res += j * (dist[j] + f[j] - f[i]);
}
ans.push_back(res);
}
}
void print()
{
for (rint i = 0; i < (int)ans.size(); i++)
{
cout << ans[i] << endl;
}
}
signed main()
{
build();
check();
calc_all_path();
print();
return 0;
}
Part4. K 短路
这种问题很麻烦,我们不妨先从次短路入手。
次短路
P2865 [USACO06NOV] Roadblocks G
我们只需要在原来 dijkstra 的模板上小改一手就可以了。
只需要再开 一个 need[] 来维护,如果 dist[y] <= x + z ,考虑 need[y] > x + z,更新答案即可。
void second_path_dijkstra()
{
memset(dist, 0x3f, sizeof dist);
memset(need, 0x3f, sizeof need);
dist[s] = 0;
q.push(make_pair(0, s));
while (!q.empty())
{
int x = -q.top().first;
int u = q.top().second;
q.pop();
for (rint i = h[u]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] > x + z)
{
need[y] = dist[y];
dist[y] = x + z;
q.push(make_pair(-dist[y], y));
q.push(make_pair(-need[y], y));
}
else if (need[y] > x + z)
{
need[y] = x + z;
q.push(make_pair(-need[y], y));
}
}
}
}
signed main()
{
cin >> n >> m;
s = 1;
for (rint i = 1; i <= m; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
second_path_dijkstra();
cout << need[n] << endl;
return 0;
}
K 短路
K 短路的求法求很多,普遍的是 \(A*\),然后堆优化。但是一般来说,不可能再考到纯 K 短路板子题了,因为一道题如果与 K 短路联合考察,数据范围还卡的很死,这道题基本不可能有人场切了,现在的出题潮流也决定了不会这么出题。所以我们只需要搞出来一个相对复杂度不是很高能大概跑过 \(n<=10^3,m<=10^4\) 的算法就可以了。
本人不喜欢这么求 K 短路。更喜欢 dp 求 K 短路。
现在,\(n\) 个点 \(m\) 条边 \(k\) 短路。数据范围同上,如何用 dp 做呢?
设\(f[i][k]\)表示:以第 \(i\) 个点为终点的第 \(k\) 短路的长度。
将序列翻转,即从 \(1\) 号点出发,到达 \(n\) 号点。
对于一条路径 \((a,b,c)\) ,从 \(a\) 转移到 \(b\)。令一个辅助数组 \(g\) ,其中 \(g[k]=f[a][k]+c\),即为从 \(a\) 点出发,到达\(y\)点的第 \(k\) 短的路的长度。因为 \(g[]\) 和 \(f[b]\) 都是递增的,直接归并。复杂度 \(O(mk)\)。
int n, m, q;
int f[N][M], g[M], h[M];
int s[M];
vector<pair<int, int> > v[M];
void calc_kth_path()
{
for (rint i = 1; i <= n; i++)
{
for (auto j : v[i])
{
for (rint k = 1; k <= s[i]; k++) g[k] = f[i][k] + j.y;
merge(g + 1, g + s[i] + 1, f[j.x] + 1, f[j.x] + s[j.x] + 1, h + 1);
s[j.x] = min(s[j.x] + s[i], q);
for (rint k = 1; k <= s[j.x]; k++) f[j.x][k] = h[k];
}
}
}
signed main()
{
cin >> n >> m >> q;
for (rint i = 1; i <= m; i++)
{
int a, b, c;
cin >> a >> b >> c;
v[b].push_back({a, c});
}
memset(f, 0x3f, sizeof f);
f[1][1] = 0;
s[1] = 1;
calc_kth_path();
for (rint i = 1; i <= q; i++)
{
cout << (f[n][i] >= inf ? -1 : f[n][i]) << endl;
}
return 0;
}
Part5. 01 最短路
01 全源
这种问题只需要对于每一个点跑一次 bfs 即可。
int n, m;
int h[M], e[M], ne[M], idx;
int dist[N][N];
queue<int> q;
void add(int a, int b)
{
e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}
void init(int n)
{
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
dist[i][j] = inf;
}
void bfs(int s)
{
dist[s][s] = 0;
q.push(s);
while(!q.empty())
{
int x = q.front();
q.pop();
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
if (dist[s][y] == inf)
{
dist[s][y] = dist[s][x] + 1;
q.push(y);
}
}
}
}
signed main()
{
build;
init(n);
for (rint i = 1; i <= n; i++) bfs(i);
return 0;
}
[CSP-S 2022] 假期计划
这道题是当初一下子把我干废的退役之题。
考试想了好久一直没有想到可以贪心,暴力还 tm 写寄了,痛失省一。
首先跑 01 全源最短路预处理所有的 dist。
然后预处理:枚举,从 \(1\) 到 \(X\) 点存在什么中途恰好去 \(1\) 个景区游玩方案,记录下前 \(3\) 优的满足距离要求的方案。
题目要求我们 \(1\to A\to B\to C\to D\to 1\),那么我们就枚举 \(B\) 和 \(C\)。
如果 \(1\to X\to B\) 和 \(C\to X\to 1\) 都分别有至少 \(3\) 种满足距离要求的方案时,枚举前 \(3\) 优解,产生的 \(9\) 种可能中,肯定有一种是四个景点互不相同的。然后根据我们枚举的 \(B\) 和 \(C\) 找答案就可以了。
int n, m, k;
int a[N];
int dist[N][N], pos[N][6], cnt[N];
int h[N], ne[M], e[M], idx;
int ans;
queue<int> q;
struct node
{
int x;
bool operator < (const node &k) const
{
return a[k.x] > a[x];
}
};
void add(int a, int b)
{
e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}
void init(int n)
{
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
dist[i][j] = inf;
}
void bfs(int s)
{
dist[s][s] = 0;
q.push(s);
while(!q.empty())
{
int x = q.front();
q.pop();
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
if (dist[s][y] == inf)
{
dist[s][y] = dist[s][x] + 1;
q.push(y);
}
}
}
}
signed main()
{
cin >> n >> m >> k;
k++;
for (rint i = 2; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; ++i)
{
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
init(n);
for (rint i = 1; i <= n; i++) bfs(i);
for (rint i = 2; i <= n; i++)
{
priority_queue<node> q;
for (rint x = 2; x <= n; x++)
{
if (x == i) continue;
if (dist[1][x] <= k && dist[x][i] <= k) q.push({x});
}
while (!q.empty() && cnt[i] < 3)
{
pos[i][++cnt[i]] = q.top().x;
q.pop();
}
}
for (rint i = 2; i <= n; i++)
{
for (rint j = i + 1; j <= n; j++)
{
if (dist[i][j] > k) continue;
for (rint k = 1; k <= cnt[i]; k++)
for (rint p = 1; p <= cnt[j]; p++)
{
int u = pos[i][k], v = pos[j][p];
if (u != j && v != i && u != v)
ans = max(ans, a[u] + a[i] + a[j] + a[v]);
}
}
}
cout << ans << endl;
return 0;
}
01 单源
[USACO08JAN] Telephone Lines S
我们以这道题为例子。
其实叫他 01 单源 并不合适,其实就是把原题目转化一个边权只为 0 或 1 的无向图。
二分最大的花费 val,然后将大于 val 的边看做权值为 \(1\) 的边,将小于等于 x 的边看做权值为零的边,然后找到从点 \(1\) 到点 \(n\) 的最短路。不断二分 check 即可。
int n, m, k;
int dist[N];
int h[N], e[M], ne[M], w[M], idx;
deque<int> q;
void add(int a, int b, int c)
{
e[++idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx;
}
bool check(int val)
{
memset(dist, 0x3f, sizeof dist);
q.clear();
dist[1] = 0;
q.push_back(1);
while (!q.empty())
{
int x = q.front();
q.pop_front();
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i] > val ? 1 : 0;
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
if(z) q.push_back(y);
else q.push_front(y);
}
}
}
if (dist[n] <= k) return 1;
return 0;
}
signed main()
{
cin >> n >> m >> k;
for (rint i = 1; i <= m; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
int l = 0, r = 1e9;
while(l < r)
{
int mid = (l + r) >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
if (l >= inf) puts("-1");
else cout << l << endl;
return 0;
}
Part6. 差分约束
模板题链接 P5960 【模板】差分约束
在遇到 \(a_{i}\le a_{j}+b\) 这样的不等式时,我们可以从 \(j\) 到 \(i\) 建一条边权为 \(b\) 的 有向边。
为了避免图不连通的情况,我们需要一个超级源点 \(n+1\) ,与点 \(i\) 之间连一条边权为 \(0\) 的边。
然后剩下的就板子了。
int n, m ,s;
int idx, h[N], ne[M], e[M], w[M], dist[N];
queue<int> q;
bool v[N];
int cnt[N];
void add(int a, int b, int c)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}
bool SPFA()
{
memset(dist, -0x3f, sizeof dist);
memset(v, 0, sizeof v);
dist[0] = 0;
v[0] = 1;
q.push(0);
cnt[0] = 0;
while (!q.empty())
{
int x = q.front();
q.pop();
v[x] = 0;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] < dist[x] + z)
{
dist[y] = dist[x] + z;
cnt[y] = cnt[x] + 1;
if (cnt[y] >= n + 1) return 1;
if (!v[y]) q.push(y), v[y] = 1;
}
}
}
return 0;
}
signed main()
{
cin >> n >> m;
s = n + 1;
for (rint i = 1; i <= m; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, -c);
}
for (rint i = 1; i <= n; i++) add(0, i, 0);
if (SPFA())
{
cout << "NO" << endl;
return 0;
}
for (rint i = 1; i <= n; i++) cout << dist[i] << " ";
return 0;
}
P4926 [1007] 倍杀测量者
对不等式进行处理
\(x_{a_i}\ge (k_i-t)\times x_{b_i}\)
\(\log_2{(x_{a_i})}\ge \log_2{(x_{b_i})}+\log_2{(k_i-t)}\)
连边 add(b,a,log2(k-t))
\((k_i+t)\times x_{a_i}>x_{b_i}\)
\(\log_2{(x_{a_i})}+\log_2{(k_i+t)}>\log_2{(x_{b_i})}\)
\(\log_2{(x_{a_i})}>\log_2{(x_{b_i})}-\log_2{(k_i+t)}\)
连边 add(b,a,-log2(k+t))
然后二分 t 就可以了
int n, s, t;
int cnt[N], typ[N];
double dist[N], w[M];
bool v[N];
int idx, h[N], e[M], ne[M];
void add(int a, int b, double c, int k)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx, typ[idx] = k;
}
bool SPFA(double val)
{
for (rint i = 0; i <= n; i++)
{
dist[i] = -inf;
cnt[i] = 0;
v[i] = 0;
}
dist[n + 1] = 0;
queue<int> q;
q.push(n + 1);
v[n + 1] = 1;
while (!q.empty())
{
int x = q.front();
q.pop();
v[x] = 0;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
double z = w[i];
if (typ[i] == 1) z = log2(w[i] - val);
if (typ[i] == 2) z = -log2(w[i] + val);
if (dist[y] < dist[x] + z)
{
dist[y] = dist[x] + z;
cnt[y] = cnt[x] + 1;
if (cnt[y] >= n + 2) return 1;
if (!v[y]) v[y] = 1, q.push(y);
}
}
}
return 0;
}
double ans, mid;
signed main()
{
double l = 0, r = 10;
cin >> n >> s >> t;
for (rint i = 0; i <= n; i++) add(n + 1, i, 0, 3);
for (rint i = 1; i <= s; i++)
{
int opt, a, b;
double x;
cin >> opt >> a >> b >> x;
add(b, a, x, opt);
if (opt == 1) r = fmin(r, x);
}
for (rint i = 1; i <= t; i++)
{
int c; double x;
cin >> c >> x;
add(0, c, log2(x), 3);
add(c, 0, -log2(x), 3);
}
if (!SPFA(0))
{
puts("-1");
return 0;
}
while (r - l > eps)
{
mid = (l + r) / 2.0;
if (SPFA(mid)) ans = mid, l = mid + eps;
else r = mid - eps;
}
printf("%.10lf", ans);
return 0;
}
Part7. 传递闭包
模板题传送门B3611 【模板】传递闭包
传统代码如下:
void closure()
{
for (rint k = 1; k <= n; k++)
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
f[i][j] |= f[i][k] & f[k][j];
}
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
cin >> f[i][j];
closure();
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= n; j++) cout << f[i][j] << ' ';
cout << endl;
}
}
发现 f[][] 数组整个都是 01 的,可以用 bitset 加速(但是在平时做题和赛时一般没必要优化)
bitset<N> f[N];
void closure()
{
for (rint j = 1; j <= n; j++)
for (rint i = 1; i <= n; i++)
if (f[i][j])
f[i] |= f[j];
}
signed main()
{
cin >> n;
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
{
int a;
cin >> a;
f[i][j] = a;//bitset不能直接cin
}
closure();
for (rint i = 1; i <= n; i++)
{
for (rint j = 1; j <= n; j++) cout << f[i][j] << ' ';
cout << endl;
}
}
P1347 排序
设定 f[i][j] 表示从 i ->j 的关系确定与否。通过 floyd 不断更新当前两点的关系。
在每次更新的时候进行 check 判断,并记录答案。
if(f[i][i] == 1) 即代表形成了一个环,即出现矛盾。
在每次 check 判断中 如果任意两点比如 i j 两点,对于 f[i][j] f[j][i]均无法确定,即代表着两者目前并未连通 即当前情况还无法确定
const int N = 3e1 + 5;
const int M = 1e3 + 5;
const int A = 1e1 - 5;
int n, m, q[M], p[M], v[N], a[N], idx, g[N];
bool f[N][N];
int calc(int x){return ((x) - 'A' + 1);}
bool cmp(int i, int j){return f[i][j];}
int check(int t)
{
memset(f, 0, sizeof f);
for (rint i = 1; i <= t; i++) f[q[i]][p[i]] = 1;
for (rint k = 1; k <= n; k++)
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
f[i][j] |= f[i][k] & f[k][j];
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
if (f[i][j] && f[j][i])
return -1;
for (rint i = 1; i <= n; i++)
for (rint j = 1; j <= n; j++)
if (i != j && !f[i][j] && !f[j][i])
return 0;
return 1;
}
signed main()
{
char s[A];
while (cin >> n >> m)
{
idx = 0;
memset(v, 0, sizeof v);
for (rint i = 1; i <= m; i++)
{
scanf("%s", s);
if (!v[calc(s[0])])
{
a[++idx] = calc(s[0]);
v[calc(s[0])] = idx;
}
if (!v[calc(s[2])])
{
a[++idx] = calc(s[2]);
v[calc(s[2])] = idx;
}
q[i] = v[calc(s[0])];
p[i] = v[calc(s[2])];
}
int res = check(m);
if (res == 0) puts("Sorted sequence cannot be determined.");
else
{
int l = 1;
int r = m + 1;
while (l < r)
{
int mid = (l + r) >> 1;
if (!check(mid)) l = mid + 1;
else r = mid;
}
if (check(l) == 1) res = 1;
if (res == -1)
{
l = 1, r = m;
while (l < r)
{
int mid = (l + r) >> 1;
if (check(mid) != -1) l = mid + 1;
else r = mid;
}
printf("Inconsistency found after %lld relations.\n", l);
}
else
{
check(l);
for (rint i = 1; i <= n; i++) g[i] = i;
sort(g + 1, g + n + 1, cmp);
printf("Sorted sequence determined after %lld relations: ", l);
for (rint i = 1; i <= n; i++) printf("%c", a[g[i]] + 'A' - 1);
puts(".");
}
}
}
return 0;
}
Part8. 同余最短路
当出现形如「给定 \(n\) 个整数,求这 \(n\) 个整数能拼凑出多少的其他整数(\(n\) 个整数可以重复取)」,以及「给定 \(n\) 个整数,求这 \(n\) 个整数不能拼凑出的最小(最大)的整数」,或者「至少要拼几次才能拼出模 \(K\) 余 \(p\) 的数」的问题时可以使用同余最短路的方法。
同余最短路利用同余来构造一些状态,可以达到优化空间复杂度的目的。
类比 差分约束 方法,利用同余构造的这些状态可以看作单源最短路中的点。同余最短路的状态转移通常是这样的 \(f(i+y) = f(i) + y\),类似单源最短路中 \(f(v) = f(u) +edge(u,v)\)。
PS:以上内容来自 OI-WIKI
好,那么好,我们以板子题目跳楼机为例子。
P3403 跳楼机
根据上面的导言,容易想到 \(f(i+y) = f(i) + y\), \(f(i+z) = f(i) + z\)
跑一个 \(dist_1 = 1\) 的 \(Dijkstra\) 的最短路
每次积累答案 \(\sum_{}{(h-dist_i) / x}\),但由于计算时除法是向下取整,注意由于 dist[] 数组的存在,是不可能出现刚好被整除的,所以要 \(+1\)
int H, x, y, z;
int idx, h[N], e[M], w[M], ne[M];
int dist[N];
bool v[N];
priority_queue<pair<int, int> > q;
void add(int a, int b, int c)
{
e[++idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}
void dijkstra(int s)
{
memset(dist, 0x3f, sizeof dist);
memset(v, 0, sizeof v);
dist[s] = 1;
q.push(make_pair(0, s));
while (!q.empty())
{
int x = q.top().second;
q.pop();
if(v[x]) continue;
v[x] = 1;
for (rint i = h[x]; i; i = ne[i])
{
int y = e[i];
int z = w[i];
if (dist[y] > dist[x] + z)
{
dist[y] = dist[x] + z;
q.push(make_pair(-dist[y], y));
}
}
}
}
signed main()
{
cin >> H >> x >> y >> z;
if (x == 1 || y == 1 || z == 1) cout << H << endl, exit(0);
for (rint i = 0; i < x; i++)
{
add(i, (i + z) % x, z);
add(i, (i + y) % x, y);
}
dijkstra(1);
int ans = 0;
for (rint i = 0; i < x; i++)
{
if (H >= dist[i]) ans += (H - dist[i]) / x + 1;
}
cout << ans << endl;
return 0;
}
[ABC077D] Small Multiple
需要用到上面提到的 01 bfs 单源
任意一个正整数都可以从 \(1\) 开始,按照某种顺序执行乘 \(10\)、加 \(1\) 的操作,最终得到,而其中加 \(1\) 操作的次数就是这个数的数位和。想到最短路。
对于所有 \(0\le k\le n-1\),从 \(k\) 向 \(10k\) 连边权为 \(0\) 的边;从 \(k\) 向 \(k+1\) 连边权为 \(1\) 的边。(点的编号均在模 \(n\) 意义下)
每个 \(n\) 的倍数在这个图中都对应了 \(1\) 号点到 \(0\) 号点的一条路径,求出 \(1\) 到 \(0\) 的最短路即可。某些路径不合法(如连续走了 \(10\) 条边权为 \(1\) 的边),但这些路径产生的答案一定不优,不影响答案。
int n;
deque<pair<int, int> > q;
bool v[N];
void bfs()
{
q.push_front(make_pair(1, 1));
while (q.size())
{
pair<int, int> x = q.front();
q.pop_front();
int a = x.first;
int b = x.second;
if (v[a]) continue;
v[a] = 1;
if (!a)
{
cout << b << endl;
return;
}
q.push_front(make_pair(a * 10 % n, b));
q.push_back(make_pair((a + 1) % n, b + 1));
}
}
signed main()
{
cin >> n;
bfs();
return 0;
}
Part9.分层图最短路
就是把图分成很多层
然后用一些边把他们连起来。用一些边权为 0 的边把他们好几层图连起来。然后建造第一层的基础上复制图层。
P4568 飞行路线
按照使用免费次数将图分为 \(0~k\) 共 \(k+1\) 层
然后跑 dijkstra 即可。不粘全部代码了,就放一下怎么建图
cin >> n >> m >> k >> s >> t;
for (rint i = 0; i < m; i++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
for (rint j = 1; j <= k; j++)
{
add(a + (j - 1) * n, b + j * n, 0);
add(b + (j - 1) * n, a + j * n, 0);
add(a + j * n, b + j * n, c);
add(b + j * n, a + j * n, c);
}
}
for (rint i = 1; i <= k; i++) add(t + (i - 1) * n, t + i * n, 0);
其余分层图基本都是板子题,在这里就不放了。只要明白底层逻辑,其他分层图难度都是较低的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号