ST 表
ST 表
定义
ST 表是用于解决 可重复贡献问题 的数据结构,通俗来说,一般可以解决区间查询问题。
区间最值和 \(gcd\)
我们以最大值为例,然后可以再推广到最小值和区间 \(gcd\)
对于$i=1$,我们可以画出这么一个图,其下标即为$j$:
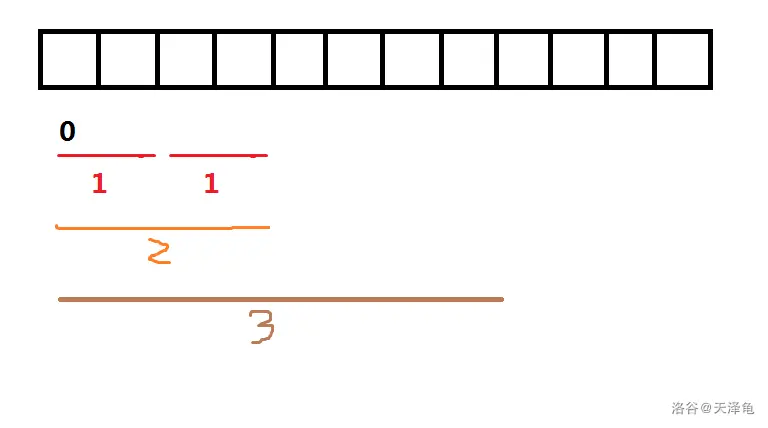
那么对于当前$i$转移其实很明显了,我们可以直接考虑将两个小区间的答案合并,即为这个大区间的值;如图中$f[1][2]$即可由$max(f[1][1],f[3][1])$转移来。
$$f[i][j]=max(f[i][j-1],f[i+2^{j-1}][j-1])$$
其中$2^{j-1}$也可写为$(1<<(j-1))$,这里位运算会更方便也会更快。
这个式子告诉我们,$ST$ 表类似于区间 $dp$,是由两个小区间合并上来的。所以应该先枚举区间长度l(这里即为$j$),再枚举$i$.
- 然后一个问题应运而生了:我们这个转移方程有没有边界呢?
不妨来看一下$i=6$的图:
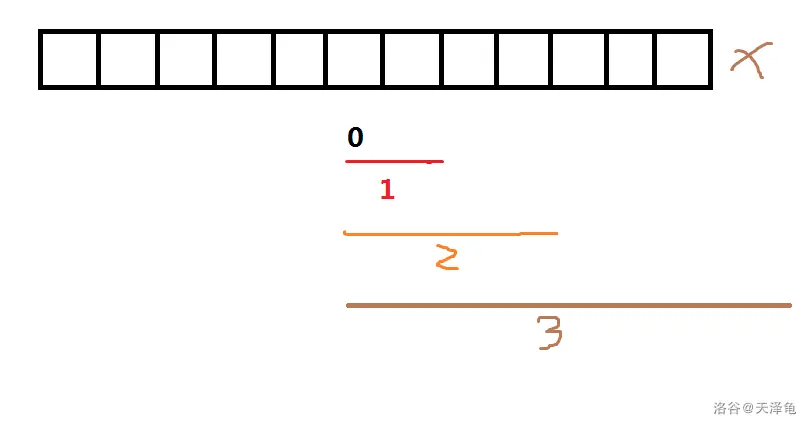
可以看出在$i=6$时,$j=3$的范围是$[6,13(6+2^3)]$,已经超出了我们数据的范畴。所以当$j=3$时,$i$只能取到$[1,5(12-2^3+1)]$
由上例再根据转移方程,不难看出当$j$确定时,$i$的范围受限在$[1,n-2^j+1]$。
我们现在来求红色标记区间$[L,R]$的最值。如果要最大化利用ST表,仍应该考虑类似处理ST表的方法,将该区间分成 两个ST表可直接维护的小区间,然后二者求最值即可。
-
那对于起始点,我们找一段ST表在该区间内可覆盖的,最大的子区间,由数学语言可描述为:
$(L+2^k-1<=R) \Leftrightarrow (k<=lg[R-L+1])$ 那我们直接取等,令$j=k$即可~
于是对于起始点点在ST表里的取值即为:$f[L][k]$
- 对于终止点,我们反向找一个与起始点要求相同的子区间,由于对称性,此时k仍为起始点求得的$k=lg[R-L+1]$
但是我们应该如何确定该子区间的起点呢?由于子区间长度为$2^k$,设起点在$D$处,则满足:
$(D+2^k-1=R) \Leftrightarrow (D=R-2^k+1)$
于是对于终止点在ST表里的取值即为:$f[D][k]$,可证明这样一定可以覆盖整个区间。
综上,对于区间$[L,R]$求其最值,不难发现答案即为:
$$\max(f[L][k],f[R-(1<<k)+1][k])$$
同理,求 \(min\) 和 \(gcd\) 的过程和以上过程是一样的,在这里附上 P3865 的代码
模板题代码
给定一个长度为 \(N\) 的数列,和 $ M $ 次询问,求出每一次询问的区间内数字的最大值。
第一行包含两个整数 \(N,M\),分别表示数列的长度和询问的个数。
第二行包含 \(N\) 个整数(记为 \(a_i\)),依次表示数列的第 \(i\) 项。
接下来 \(M\) 行,每行包含两个整数 \(l_i,r_i\),表示查询的区间为 \([l_i,r_i]\)。
输出包含 \(M\) 行,每行一个整数,依次表示每一次询问的结果。
#include <bits/stdc++.h>
#define rint register int
#define endl '\n'
using namespace std;
const int N = 1e6 + 5;
const int M = 2e1 + 1;
int n, m;
int gcd_[N][M];
int maxx[N][M];
int minn[N][M];
int gcd(int a, int b)
{
if (!b) return a;
return gcd(b, a % b);
}
int query_gcd(int l, int r, int *a)
{
int k = log2(r - l + 1);
return gcd(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
int query_max(int l, int r, int *a)
{
int k = log2(r - l + 1);
return max(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
int query_min(int l, int r, int *a)
{
int k = log2(r - l + 1);
return min(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
signed main()
{
cin >> n >> m;
for (rint i = 1; i <= n; i++)
{
int k;
cin >> k;
maxx[i][0] = k;
minn[i][0] = k;
gcd_[i][0] = k;
}
for (rint j = 1; j <= M; j++)
{
for (rint i = 1; i + (1 << j) - 1 <= n; i++)
{
int k = i + (1 << (j - 1));
maxx[i][j] = max(maxx[i][j - 1], maxx[k][j - 1]);
minn[i][j] = min(minn[i][j - 1], minn[k][j - 1]);
gcd_[i][j] = gcd(gcd_[i][j - 1], gcd_[k][j - 1]);
}
}
for (rint i = 1; i <= m; i++)
{
int l, r;
cin >> l >> r;
cout << query_max(l, r, (int *)maxx) << endl;
//cout << query_min(l, r, (int *)minn) << endl;
//cout << query_gcd(l, r, (int *)gcd_) << endl;
}
return 0;
}
[NOI2010] 超级钢琴
有 $n$ 个音符,编号为 $1$ 至 $n$ 。第 $i$ 个音符的美妙度为 $A_i$ 。
我们要找到 $k$ 段超级和弦组成的乐曲,每段连续的音符的个数 $x$ 满足 $L\leq x\leq R$ ,求乐曲美妙度的最大值。
首先,对于一段区间在左端点固定的情况下它的取值范围为 $sum[i + k]-sum[i - 1]\sim sum[i + k]-sum[i-1]$ 之间,$k\subseteq [l, r]$.所以,我们只需让前面一项最大即可。
ST 表维护一个前缀最大值,让后,每次取出使区间和最大的端点,再用前缀和计算区间和。这里用优先队列可以做到这点,同时用类似 ST 表的方法维护一个区间和最大的端点。
再考虑,由于不能出现两个相同的区间,所以取完一个区间后,设 $now$ 为选择的节点,它会分裂成两个区间。即 $l\sim now - 1$ 和 $now + 1\sim r$。判断是否合法之后加入优先队列,取 $k$ 次,就是最大值。
#include <bits/stdc++.h>
#define rint register int
#define int long long
#define endl '\n'
using namespace std;
const int N = 5e5 + 5;
const int M = 2e1 + 1;
int n, m, L, R;
int a[N], s[N];
int f[N][M];
int ans;
struct node
{
int l, r, p, q;
//p 是左端点, l 和 r 是右端点的范围, q 是当前解的右端点的位置
bool operator < (const node &x) const
{
return s[x.q] - s[x.p] > s[q] - s[p];
}
};
priority_queue<node> q;
int max(int a, int b)
{
return a > b ? a : b;
}
int min(int x, int y)
{
return s[x] < s[y] ? x : y;
}
int query_min(int l, int r, int *a)
{
int k = log2(r - l + 1);
return min(a[l * M + k], a[(r - (1 << k) + 1) * M + k]);
}
signed main()
{
cin >> n >> m >> L >>R;
for (rint i = 1; i <= n; i++)
{
cin >> a[i];
}
for (rint i = 1; i <= n; i++)
{
s[i] = s[i - 1] + a[i];
f[i][0] = i;
}
for (rint j = 1; j <= M; j++)
{
for (rint i = 0; i + (1 << j) - 1 <= n; i++)
//如果你在前面找最小值, ST 表要从 0 开始初始化
{
int k = i + (1 << (j - 1));
f[i][j] = min(f[i][j - 1], f[k][j - 1]);
}
}
for (rint i = L; i <= n; i++)
{
int r = i - L;
int l = max(0, i - R);
q.push({l, r, query_min(l, r, (int *)f), i});
}
for (rint i = 1; i <= m; i++)
{
node k = q.top();
q.pop();
ans += s[k.q] - s[k.p];
int l = k.l;
int r = k.p - 1;
if (l <= r)
{
q.push({l, r, query_min(l, r, (int *)f), k.q});
}
l = k.p + 1;
r = k.r;
if (l <= r)
{
q.push({l, r, query_min(l, r, (int *)f), k.q});
}
}
cout << ans << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号