块状链表
块状链表
对于线性表，可以 \(O(1)\) 的访问，但是插入和删除操作是 \(O(n)\)
对于链表，可以 \(O(1)\) 的进行插入和删除，但是是 \(O(n)\) 的访问。
于是本着分块的思想，有了块状链表 。
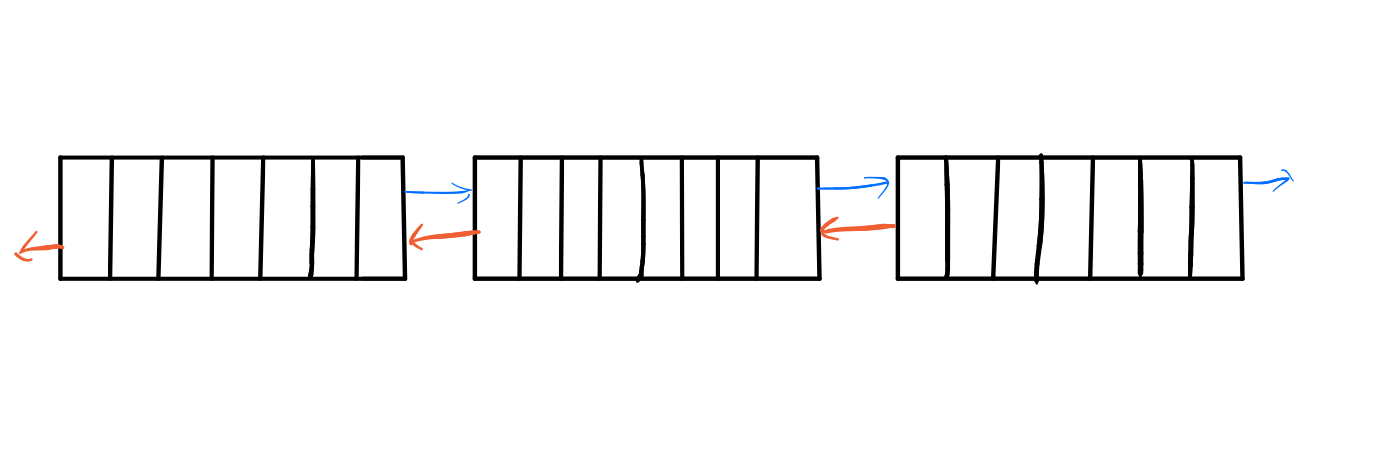
大概长这个样子。每个块的大小数量级在 $ O(\sqrt n)$ , 块数的量级 $ O(\sqrt n)$
主要有以下几种操作：
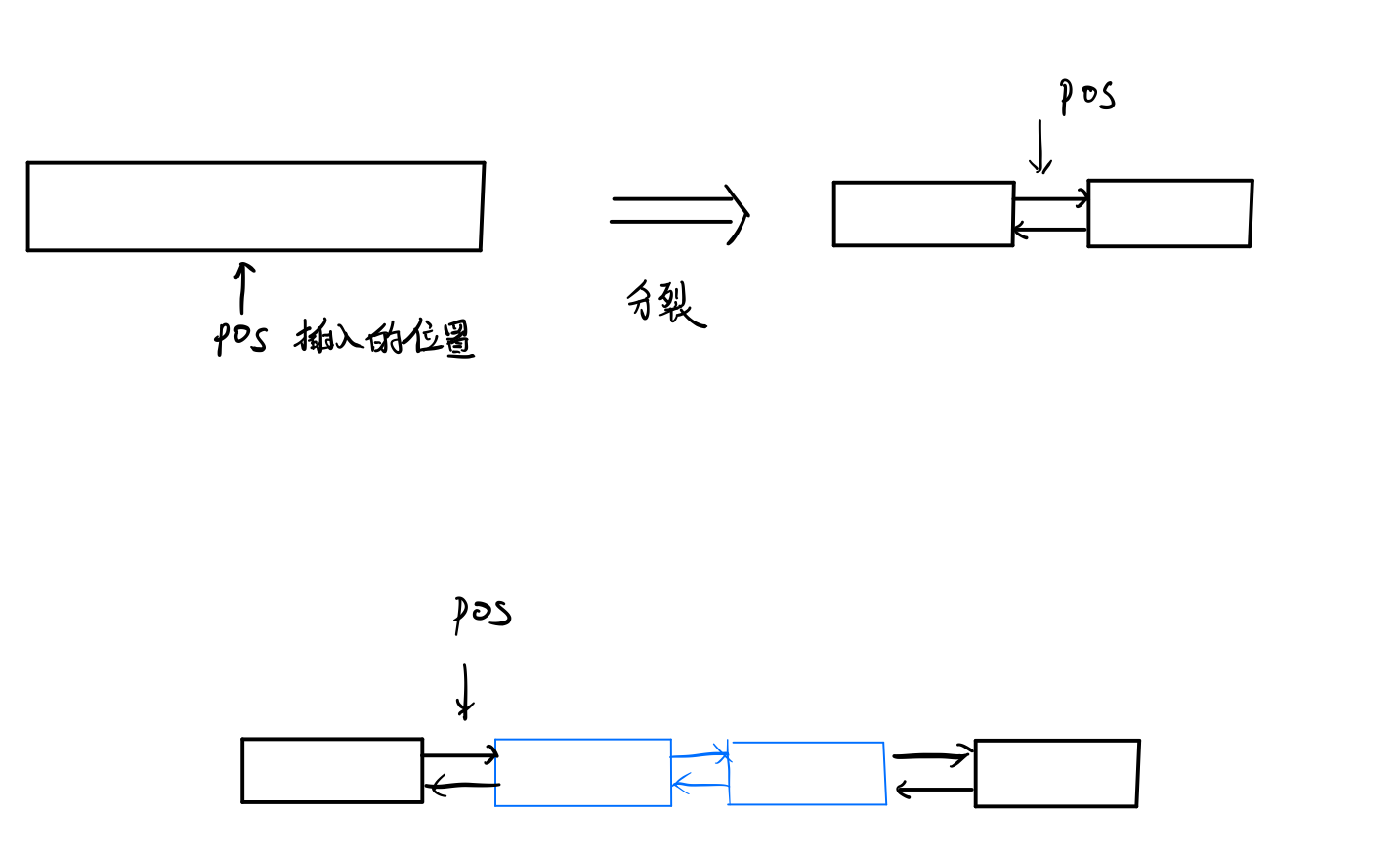
插入
-
分裂节点 $ O(\sqrt n)$
-
在分裂点插入 $ O(\sqrt n)$
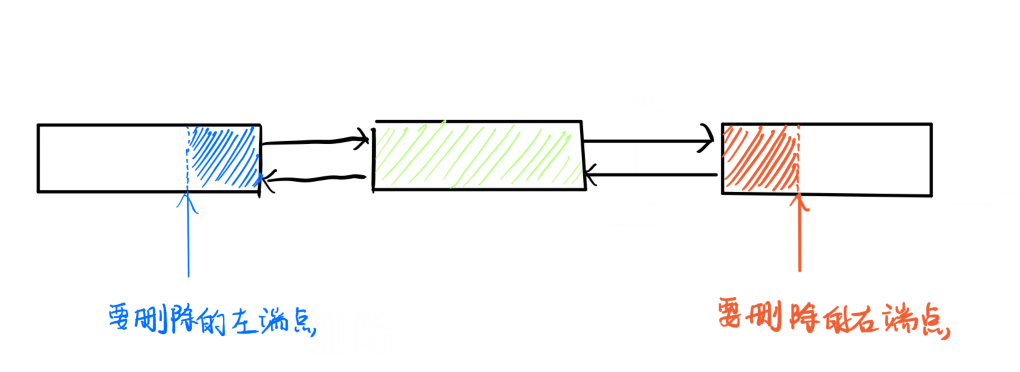
删除
-
删除开头节点的后半部分 $ O(\sqrt n)$
-
删除中心完整节点 $ O(\sqrt n)$
-
删除结尾节点的前半部分 $ O(\sqrt n)$
合并
为了保证正确的复杂度，要不定期的进行合并操作。
所谓合并操作，就是从第一个块开始，如果把下一个块合并过来之后大小不大于 $ O(\sqrt n)$，就把两个块合并
若没有合并操作，则可能会有很多小块，导致 TLE
例题 P4008 [NOI2003] 文本编辑器
//别开 long long
#include <bits/stdc++.h>
#define rint register int
#define endl '\n'
using namespace std;
const int N = 2e3;
const int M = 2e3 + 1e1;
const int Q = 2e6 + 1e1;
int n, x, y;
struct Node
{
char s[N + 1];
int c, l, r;
} p[M];
char str[Q];
int q[M], tt; // 内存回收
void move(int k) // 移到第k个字符后面
{
x = p[0].r;
while (k > p[x].c)
k -= p[x].c, x = p[x].r;
y = k - 1;
return;
}
void add(int x, int u) // 将节点u插到节点x的右边
{
p[u].r = p[x].r;
p[p[u].r].l = u;
p[x].r = u;
p[u].l = x;
return;
}
void del(int u) // 删除节点u
{
p[p[u].l].r = p[u].r;
p[p[u].r].l = p[u].l;
p[u].l = p[u].r = p[u].c = 0; // 清空节点u
q[++tt] = u; // 回收节点u
return;
}
void insert(int k) // 在光标后插入k个字符
{
if (y < p[x].c - 1) // 从光标处分裂
{
int u = q[tt--]; // 新建一个节点
for (rint i = y + 1; i < p[x].c; i++)
p[u].s[p[u].c++] = p[x].s[i];
p[x].c = y + 1;
add(x, u);
}
int cur = x;
for (rint i = 0; i < k;)
{
int u = q[tt--]; // 创建一个新的块
while (p[u].c < N && i < k)
p[u].s[p[u].c++] = str[i++];
add(cur, u);
cur = u;
}
return;
}
void remove(int k) // 删除光标后的k个字符
{
if (p[x].c - 1 - y >= k) // 节点内删
{
for (rint i = y + k + 1, j = y + 1; i < p[x].c; i++, j++)
p[x].s[j] = p[x].s[i];
p[x].c -= k;
}
else
{
k -= p[x].c - y - 1; // 删除当前节点的剩余部分
p[x].c = y + 1;
while (p[x].r && k >= p[p[x].r].c)
{
int u = p[x].r;
k -= p[u].c;
del(u);
}
int u = p[x].r; // 删除结尾节点的前半部分
for (rint i = 0, j = k; j < p[u].c; i++, j++)
p[u].s[i] = p[u].s[j];
p[u].c -= k;
}
return;
}
void get(int k) // 返回从光标开始的k个字符
{
if (p[x].c - 1 - y >= k) // 节点内返回
{
for (rint i = 0, j = y + 1; i < k; i++, j++)
putchar(p[x].s[j]);
}
else
{
k -= p[x].c - y - 1;
for (rint i = y + 1; i < p[x].c; i++)
putchar(p[x].s[i]); // 输出当前节点的剩余部分
int cur = x;
while (p[cur].r && k >= p[p[cur].r].c)
{
int u = p[cur].r;
for (int i = 0; i < p[u].c; i++)
putchar(p[u].s[i]);
k -= p[u].c;
cur = u;
}
int u = p[cur].r;
for (rint i = 0; i < k; i++)
putchar(p[u].s[i]);
}
puts("");
return;
}
void prev() // 光标向前移动一位
{
if (!y)
{
x = p[x].l;
y = p[x].c - 1;
}
else
y--;
return;
}
void next() // 光标向后移动一位
{
if (y < p[x].c - 1)
y++;
else
{
x = p[x].r;
y = 0;
}
return;
}
void merge() // 将长度较短的相邻节点合并，保证块状链表时间复杂度的核心
{
for (rint i = p[0].r; i; i = p[i].r)
{
while (p[i].r && p[i].c + p[p[i].r].c < N)
{
int r = p[i].r;
for (int j = p[i].c, k = 0; k < p[r].c; j++, k++)
p[i].s[j] = p[r].s[k];
if (x == r)
x = i, y += p[i].c; // 更新光标的位置
p[i].c += p[r].c;
del(r);
}
}
return;
}
signed main()
{
for (rint i = 1; i < M; i++)
q[++tt] = i;
cin >> n;
char op[10];
str[0] = '>';
insert(1); // 插入哨兵
move(1); // 将光标移动到哨兵后面
while (n--)
{
int a;
cin >> op;
if (!strcmp(op, "Move"))
{
cin >> a;
move(a + 1);
}
else if (!strcmp(op, "Insert"))
{
cin >> a;
int i = 0, k = a;
while (a)
{
str[i] = getchar();
if (str[i] >= 32 && str[i] <= 126)
i++, a--;
}
insert(k);
merge();
}
else if (!strcmp(op, "Delete"))
{
cin >> a;
remove(a);
merge();
}
else if (!strcmp(op, "Get"))
{
cin >> a;
get(a);
}
else if (!strcmp(op, "Prev"))
prev();
else
next();
}
return 0;
}
