扫描线

关于扫描线

基础是求周长并和面积并的算法。

注意，扫描线是一条不存在的线。

假设有一条扫描线从一个图形的下方扫向上方（或者左方扫到右方），那么通过分析扫描线被图形截得的线段就能获得所要的结果。

实现扫描线

这里将出现的所有矩形以横坐标为分割线划分成一个个竖直的长条，计算每个长条的面积，相加就可以得到答案，如下图：

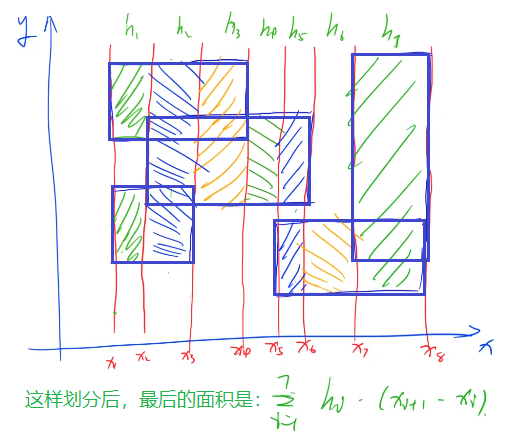
每个长条内部都是一堆等宽的小矩形，我们求出这些矩形在竖直方向上的长度，然后乘以宽度就是这个长条的面积。

如何求解每个长条竖直方向上的长度之和呢？首先遍历所有矩形，找到这个长条中所有的线段，然后使用区间合并即可。

时空复杂度 \(O(n^2×log\) \(n)\)

//关于此题卡掉了yxc STl做法。。。。 
#include<bits/stdc++.h>

#define int long long
#define rint register int
#define endl '\n' 

using namespace std;
const int N = 2e5 + 5;

#define find(x) lower_bound(a+1,a+1+k,x)-a

int n,xx1,yy1,xx2,yy2,a[N],k,ans;

struct node{int x,yy1,yy2,v;friend bool operator<(node i,node j){return i.x<j.x;}}line[N];
int l[N],r[N],sum[N],tot[N];

void build(int i,int lt,int rt){
	l[i]=lt;r[i]=rt;
	if(lt==rt) return;
	int m=(lt+rt)>>1;
	build(i<<1,lt,m);
	build(i<<1|1,m+1,rt);
	return ;
}

void update(int i){
	sum[i]=tot[i]?a[r[i]+1]-a[l[i]]:sum[i<<1]+sum[i<<1|1];
	return ;
}

void fix(int i,int x,int y,int z){
	if(l[i]>y||r[i]<x) return;
	if(x<=l[i]&&y>=r[i]){tot[i]+=z;update(i);return;}
	fix(i<<1,x,y,z);fix(i<<1|1,x,y,z);update(i);
	return ;
}

signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>xx1>>yy1>>xx2>>yy2;
		a[(i<<1)-1]=yy1;a[i<<1]=yy2;
		line[(i<<1)-1].x=xx1;line[i<<1].x=xx2;
		line[(i<<1)-1].v=1;line[i<<1].v=-1;
		line[(i<<1)-1].yy1=line[i<<1].yy1=yy1;
		line[(i<<1)-1].yy2=line[i<<1].yy2=yy2;
	}
	n<<=1;
	
	sort(line+1,line+1+n);
	sort(a+1,a+1+n);
	k=unique(a+1,a+1+n)-a-1;
	
	build(1,1,k-1);
	
	for(rint i=1;i<=n;i++){
		ans+=1ll*(line[i].x-line[i-1].x)*sum[1];
		fix(1,find(line[i].yy1),find(line[i].yy2)-1,line[i].v);
	}
	
	cout<<ans<<endl;
	
	return 0;
}