[动态树] Link-Cut Tree

Link-Cut Tree

0x00 绪言

学长们讲 LCT 的时候，我在另一个机房摸鱼，所以没有听到，就回家看 yxc 的补了补。

0x01 什么是动态树

动态树问题, 即要求我们维护一个由若干棵子结点无序的有根树组成的森林，支持对树的分割, 合并, 对某个点到它的根的路径的某些操作, 以及对某个点的子树进行的某些操作。简单来说，动态树就是可以在部分树链剖分的功能上支持换根，断开树上一条边，连接两个点，保证连接后仍然是一棵树这类操作。

0x02 常用概念

偏爱儿子 ：偏爱儿子与父亲节点同在一棵平衡树中，一个节点最多只能有一个偏爱儿子；

实边 ：连接父亲节点和偏爱儿子的边；

偏爱路径 ：由实边及实边连接的节点构成的链；

辅助树 ：由一条偏爱路径上的所有节点所构成的 Splay 称作这条链的辅助树。每个点的键值为这个点的深度，即这棵 Splay 的中序遍历是这条链从链顶到链底的所有节点构成的序列。辅助树的根节点的父亲指向链顶的父亲节点，然而链顶的父亲节点的儿子并不指向辅助树的根节点。

0x03 实链剖分

• 对于一个点连向它所有儿子的边, 我们自己选择一条边进行剖分，我们称被选择的边为实边，其他边则为虚边。

• 对于实边，我们称它所连接的儿子为实儿子。

• 对于一条由实边组成的链，同样称之为实链。

• 对于每条实链，我们分别建一个平衡树来维护整个链区间的信息

0x04 辅助树和原树的关系

• 原树中的实链在辅助树中都在同一颗平衡树里

• 原树中的虚链 : 在辅助树中，子节点所在平衡树的父亲 指向 父节点，但是父节点的两个儿子都不指向子节点。

• 原树的父亲指向不等于 辅助树的父亲指向。

• 辅助树是可以在满足辅助树、平衡树的性质下任意换根的。

• 虚实链变换可以轻松在辅助树上完成，这也就是实现了动态维护树链剖分。

0x05 yxc 图解

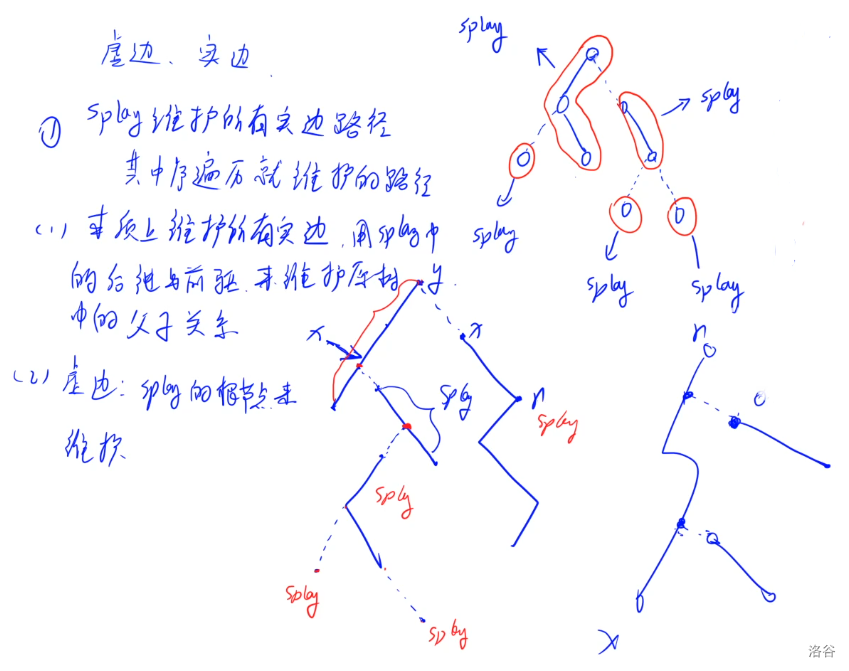
0x06 时空复杂度

LCT 的时间复杂度为单次操作均摊 O(log n)，整体空间复杂度为 O(n)。

0x07 函数代码实现（于2022.7.13 23:46更新）

ljx 学长觉得这篇博客写的不好，确实，少了精髓，现在补上。（好困呐 QWQ）

我们就以 luogu 模板题 【模板】动态树 为例子

push_up

push_up(x)：本题需要维护的是路径的异或和

void push_up(int p)
{
    t[p].size = t[t[p].s[1]].size ^ t[t[p].s[0]].size ^ t[p].val;
}

push_down

push_down(p)：不同于翻转区间那题，这里懒标记维护的是修改后的懒标记

void filp(int x)
{
    std::swap(t[x].s[0], t[x].s[1]);
    t[x].tag ^= 1;
}
void push_down(int p)
{
    if (!t[p].tag)
    {
        return;
    }
    t[p].tag = 0;
    if (t[p].s[0])
        filp(t[p].s[0]);
    if (t[p].s[1])
        filp(t[p].s[1]);
}

rotate

rotate(int x)：在修改 z 与 y 这条边的时候特判 y 是否为根节点

原本 splay 的根节点应该是没有父节点的，但 LCT 里我们让这个空指针来维护虚边

get(x) 函数后面会介绍

int get(int x)
{
    return t[t[x].fa].s[0] == x || t[t[x].fa].s[1] == x;
}
void rotate(int x)
{
    int y = t[x].fa;
    int z = t[y].fa;
    int k = t[y].s[1] == x;
    int v = t[x].s[k ^ 1];
    if (get(y))
    {
        t[z].s[t[z].s[1] == y] = x;
    }
    t[x].s[k ^ 1] = y;
    t[y].s[k] = v;
    if (v)
    {
        t[v].fa = y;
    }
    t[y].fa = x;
    t[x].fa = z;
    push_up(y);
}

splay

splay(int x)：把节点 x 转到辅助树 splay 的根节点

我先说一下这里不同的地方，以往 splay 找某个节点的时候，都是从根节点往下找（按照 BST 的性质）

但是在 LCT 中，splay 充当的是辅助树的角色，我们获得 splay 中的节点是通过原树中对应节点的编号

换而言之，我们是直接获得 splay 中的某个节点，而不是自上而下递归找到的

所以，在做 splay 转到根节点的旋转操作时，我们需要先自上而下把懒标记下传

这就是与传统 splay 相矛盾的地方

void splay(int x)
{
    int y = x;
    int top = 0;
    stk[++top] = y;
    while (get(y))
    {
        stk[++top] = y = t[y].fa;
    }
    while (top != 0)
    {
        push_down(stk[top--]);
    }
    while (get(x))
    {
        y = t[x].fa;
        top = t[y].fa;
        if (get(y))
        {
            rotate((t[y].s[0] == x) ^ (t[top].s[0] == y) ? x : y);
        }
        rotate(x);
    }
    push_up(x);
}

access

access(x) ：建立一条从根节点到 x 的实链（同时将 x 变成对应 splay 的根节点）

• 把当前节点转到根。
• 把儿子换成之前的节点。
• 更新当前点的信息。
• 把当前点换成当前点的父亲，继续操作。

void access(int x)
// 建立一条从根节点到 x 的实链（同时将 x 变成对应 splay 的根节点）
{
    for (rint y = 0; x; x = t[y = x].fa) // x沿着虚边往上找根
    {
        splay(x); // 先转到当前辅助树的根
        t[x].s[1] = y;
        push_up(x); // 把上个树接到中序遍历后面
    }
}

makeroot

makeroot(x) 将 x 变成原树的根节点

access(x) 操作之后，x 会被旋转到splay的树根，此时我们只需反转 x，就可以达到反转 splay 中序遍历的效果

而 splay 中序遍历被反转，也就意味着原树中，从根节点到 x 的路径被反转，从而实现把 x 变成根的操作

void makeroot(int x)
// 将 x 变成原树的根节点（且左子树为空）
{
    access(x); 
    splay(x);
    filp(x);
}

findroot

findroot(x) ：找到 x 所在的原树的根节点，再将原树的根节点旋转到辅助树的根节点

先 access(x) 打通从根节点到 x 的实链（此时 x 在 splay 的根节点），然后找到该 splay 中序遍历的第一个节点

int findroot(int x)
// 找到 x 所在的原树的根节点，再将原树的根节点旋转到辅助树的根节点
{
    access(x);
    // 打通根节点到 x 的实链，当前 x 位于辅助树的根节点位置
    splay(x);
    while (t[x].s[0])
    {
        push_down(x);
        x = t[x].s[0];
    } // 找到辅助树中序遍历的第一个元素（左下角）
    return x;
}

split

split(x, y) ：将 x 到 y 的路径变为实边路径

比较简单，先把 x 放到根，再打通从 根 到 y 的路径即可

void split(int x, int y)
// 将 x 到 y 的路径变为实边路径
{
    makeroot(x);
    // 先把 x 设为根
    access(y);
    // 在打通根到 y 的实链即可
    splay(y);
}

link

link(x, y) ：若 x , y 不连通，则加入 (x, y) 这条边

先把 x 放到根，查找一下 y 所在树的根节点是不是 x。

如果不是（查找根节点会把 y 转到他辅助树的根节点）则加边

void link(int x, int y)
// 若 x , y 不连通，则加入 (x, y) 这条边
{
    makeroot(x);
    // 先把 x 设为根
    if (findroot(y) != x)
    {
        t[x].fa = y;
        // 如果不连通，则把 x 的实链接到 y 上即可
    }
}

cut

cut(x, y) ：若边 (x, y) 存在，则删掉（x, y）这条边

先把 x 放到根，判断此时：

• y 所在的原树中的根是否是 x
• y 的父节点是否是根 x
• y 是否有左孩子（中序遍历紧挨在 x 的后面）

满足上述三条，说明 边 (x,y) 存在，cut 掉

void cut(int x, int y)
// 若边 (x, y) 存在，则删掉（x, y）这条边
{
    makeroot(x);
    if (findroot(y) == x && t[x].fa == y && !t[x].s[1])
    {
        t[x].fa = t[y].s[0] = 0;
        push_up(y);
    }
}

get

get(x) ：判断 x 是否是所在辅助树 splay 的根节点

这个比较简单，按照我们之前所说的，他有父亲，但他父亲不认他

int get(int x)//判断 x 是否为实链的顶部
{
    return t[t[x].fa].s[0] == x || t[t[x].fa].s[1] == x;
}

0x08 代码实现

给定 \(n\) 个点以及每个点的权值，要你处理接下来的 \(m\) 个操作。
操作有四种，操作从 \(0\) 到 \(3\) 编号。点从 \(1\) 到 \(n\) 编号。

• 0 x y 代表询问从 \(x\) 到 \(y\) 的路径上的点的权值的 \(\text{xor}\) 和。保证 \(x\) 到 \(y\) 是联通的。
• 1 x y 代表连接 \(x\) 到 \(y\)，若 \(x\) 到 \(y\) 已经联通则无需连接。
• 2 x y 代表删除边 \((x,y)\)，不保证边 \((x,y)\) 存在。
• 3 x y 代表将点 \(x\) 上的权值变成 \(y\)。

输入格式

第一行两个整数，分别为 \(n\) 和 \(m\)，代表点数和操作数。

接下来 \(n\) 行，每行一个整数，第 \((i + 1)\) 行的整数 \(a_i\) 表示节点 \(i\) 的权值。

接下来 \(m\) 行，每行三个整数，分别代表操作类型和操作所需的量。

输出格式

对于每一个 \(0\) 号操作，你须输出一行一个整数，表示 \(x\) 到 \(y\) 的路径上点权的 \(\text{xor}\) 和。

对于全部的测试点，保证：

• \(1 \leq n \leq 10^5\)，\(1 \leq m \leq 3 \times 10^5\)，\(1 \leq a_i \leq 10^9\)。
• 对于操作 \(0, 1, 2\)，保证 \(1 \leq x, y \leq n\)。
• 对于操作 \(3\)，保证 \(1 \leq x \leq n\)，\(1 \leq y \leq 10^9\)。

#include <iostream>
#include <cstdio>
#include <algorithm>

#define rint register int
#define endl '\n'

const int N = 3e5 + 2;

struct Link_Cut_Tree
{
    struct node
    {
        int s[2], fa;
        int val;
        int size;
        bool tag;
    } t[N];

    int get(int x)
    {
        return t[t[x].fa].s[0] == x || t[t[x].fa].s[1] == x;
    }

    void push_up(int p)
    {
        t[p].size = t[t[p].s[1]].size ^ t[t[p].s[0]].size ^ t[p].val;
    }

    void filp(int x)
    {
        std::swap(t[x].s[0], t[x].s[1]);
        t[x].tag ^= 1;
    }

    void push_down(int p)
    {
        if (!t[p].tag)
        {
            return;
        }
        t[p].tag = 0;
        if (t[p].s[0])
            filp(t[p].s[0]);
        if (t[p].s[1])
            filp(t[p].s[1]);
    }

    void rotate(int x)
    {
        int y = t[x].fa;
        int z = t[y].fa;
        int k = t[y].s[1] == x;
        int v = t[x].s[k ^ 1];
        if (get(y))
        {
            t[z].s[t[z].s[1] == y] = x;
        }
        t[x].s[k ^ 1] = y;
        t[y].s[k] = v;
        if (v)
        {
            t[v].fa = y;
        }
        t[y].fa = x;
        t[x].fa = z;
        push_up(y);
    }

    int stk[N];

    void splay(int x)
    {
        int y = x;
        int top = 0;
        stk[++top] = y;
        while (get(y))
        {
            stk[++top] = y = t[y].fa;
        }
        while (top != 0)
        {
            push_down(stk[top--]);
        }
        while (get(x))
        {
            y = t[x].fa;
            top = t[y].fa;
            if (get(y))
            {
                rotate((t[y].s[0] == x) ^ (t[top].s[0] == y) ? x : y);
            }
            rotate(x);
        }
        push_up(x);
    }

    void access(int x)
    {
        for (rint y = 0; x; x = t[y = x].fa)
        {
            splay(x);
            t[x].s[1] = y;
            push_up(x);
        }
    }

    void makeroot(int x)
    {
        access(x);
        splay(x);
        filp(x);
    }

    int findroot(int x)
    {
        access(x);
        splay(x);
        while (t[x].s[0])
        {
            push_down(x);
            x = t[x].s[0];
        }
        return x;
    }

    void split(int x, int y)
    {
        makeroot(x);
        access(y);
        splay(y);
    }

    void link(int x, int y)
    {
        makeroot(x);
        if (findroot(y) != x)
        {
            t[x].fa = y;
        }
    }

    void cut(int x, int y)
    {
        makeroot(x);
        if (findroot(y) == x && t[x].fa == y && !t[x].s[1])
        {
            t[x].fa = t[y].s[0] = 0;
            push_up(y);
        }
    }
} tree;

int n, m;

int main()
{
    scanf("%d%d", &n, &m);

    for (rint i = 1; i <= n; i++)
    {
        scanf("%d", &tree.t[i].val);
    }

    while (m--)
    {
        int op, x, y;
		scanf("%d%d%d", &op, &x, &y);
        if (op == 0)
        {
            tree.split(x, y);
            printf("%d\n", tree.t[y].size);
        }
        if (op == 1)
        {
            tree.link(x, y);
        }
        if (op == 2)
        {
            tree.cut(x, y);
        }
        if (op == 3)
        {
            tree.splay(x);
            tree.t[x].val = y;
        }
    }
    return 0;
}