网络流--基础概念
流网络
带权的有向图 G=(V,E),满足以下条件,则称为网络流图:
- 仅有一个入度为
0的顶点s,称s为源点 - 仅有一个出度为
0的顶点t,称t为汇点 - 每条边的权值都为非负数,称为该边的容量,记作
c(i,j)。
我们来随便画一个小图
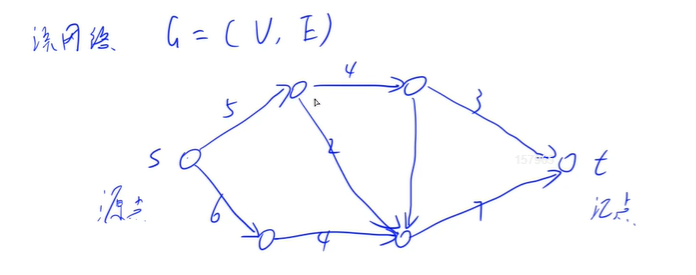
这个东西可以理解成什么呢,源点s是一个水库,一个无尽水的水库,然后我们把水往外面通,每条边是一个管道,c就是每个管道可以流过水的速度的最大限制。
可行流
过容量网络G中每条弧 <u,v>,上的实际流量(简称流量),记为f(u,v);
流量限制
由于流量是实际的,而c只是最大限制,我们就可以得到一个限制:
PS:除了源点汇点其他点不会存储流量,流进来多少,流出去多少。
流量守恒
对于一个点x,流进x的流量之和和从x出去的流量之和是一样的。
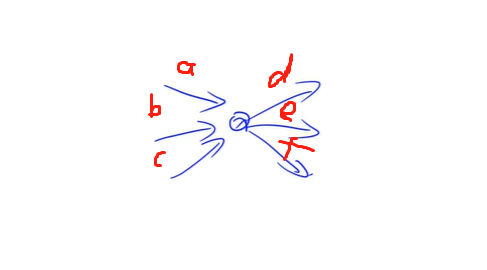
我们设此图中流进来的流量为a,b,c流出去的为d,e,f
则:\(a+b+c=d+e+f\)
就是这个意思。
当然,方便理解,目前完全不考虑反向边
啊有人就要问了:
我在网上看到了!反对称性,对任意u,v∈V,f(u,v) = -f(v,u)。从u到v的流量一定是从v到u的流量的相反值!要考虑反向边!
首先,目前不考虑仅仅是方便理解,之所以不加反向边是因为,我们定义的f不小于零,然后f(u,v) = -f(v,u)?当然,有的博客讲的是可以为负数的,我们就按流量为正数,参考《算法导论》理解。因为算导不容易坑爹.......
然后关于如何处理反向边,就算遇到了,也很好办啊!

我们在下面加一个点。

就解决了!
流量值
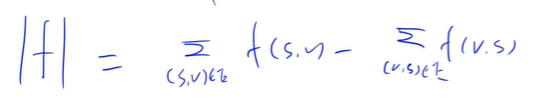
我们用 \(|f|\) 表示流量值,即每秒进网络流的流量。
最大流
对于每一个可行流,我们都可以求对应的一个流量值。
我们讲这些流量值存进一个集合S,网络流就是集合S中最大的那个流量值。
所以最大流指的是最大可行流
残留网络
残留网络是针对流网络中的某一条可行流来说的。通常用 \(G_f\) 表示。
它是怎么定义的呢?
首先它的点集和原来是完全一样的 \(V_f = V\),每个点和原图的每个点一样;
它的边集是原来的两倍 \(E_f = E + E\)中的所有反向边;
那残留网络有什么别的特点呢?
它可以退流。
所以它的容量定义也与众不同。
当(u,v)∈E时,\(c'(u,v)=c(u,v)-f(u,v)\)
当(v,u)∈E时,\(c'(u,v)=f(v,u)\)
我们来画一个残留网络
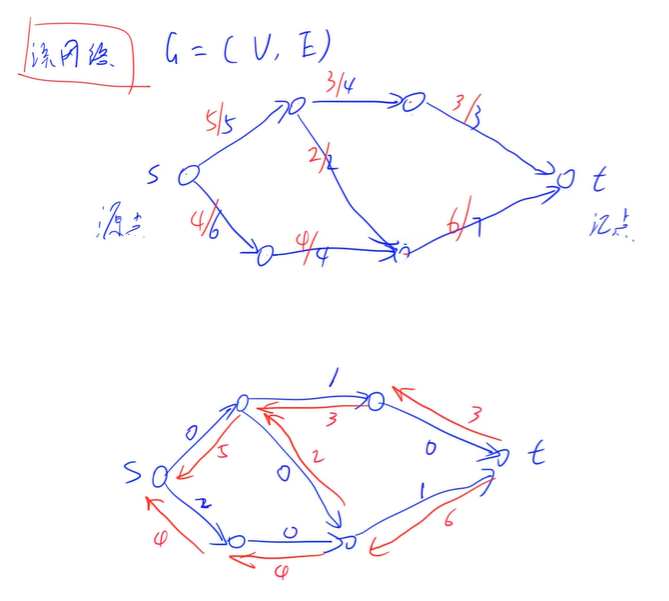
当然,这里有一个定理
文字叙述:原网络的可行流加上它对应网络的一个可行流的结构也是原网络的一个可行流
\(f+f'\) 也是 \(G\) 的一个可行流!
计算:\(|f+f'|=|f|+|f'|\)(流量相加是指每条边对应相加,即正方向的加上,反方向的减去,类似于数学中的向量)
推论1:如果我们残留网络里是有可行流的话,且可行流流量大于零,那么我们原网络的那个可行流一定不是最大流
推论2:残留网络里没有可行流,则原网络的那个可行流一定是最大流
增广路径
在残留网络里面,从源点出发,沿着容量大于零的边,如果能够走到终点的话,那么这条路径就被称为增广路径。
即增广路径就是残留网络的可行流
定理:如果对于当前的可行流 f 来说,在它的残留网络 \(G_f\) 里,如果没有增广路径的话,我们就可以断定,f是一个最大流。
割
割指的是一个在G=(V,E)中的点,将V拆成两个集合S,T,使得源点在S,汇点在T。
割的容量
我们把所有横跨两个集合的,有向的,且S指向T的边的容量之和把它计为割的容量。
割的流量
我们把所有横跨两个集合的从S流向T的容量减去从T到S的的容量计为割的流量。

性质
性质1;对于流网络的任意一个可行流,任意一个割,它的流量值等于割的流量。即 \(|f|=f(S,T)\)
性质2;对于流网络的任意一个可行流,任意一个割,它的流量值小于等于割的容量。即 \(|f|≤C(S,T)\)
最小割
最小割是指所有割里最小的割容量
最大流最小割定理
最大流最小割定理是网络流理论的重要定理。是指在一个网络流中,能够从源点到达汇点的最大流量等于如果从网络中移除就能够导致网络流中断的边的集合的最小容量和。
即在任何网络中,最大流的值等于最小割的容量。
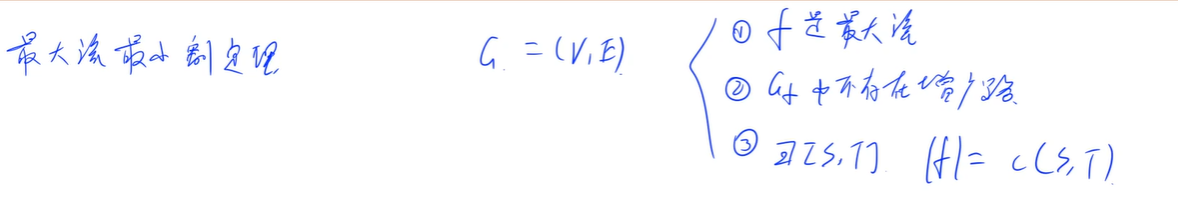



 浙公网安备 33010602011771号
浙公网安备 33010602011771号