二维凸包

本文由于方便理解，代码中变量名称较长

什么是凸包？

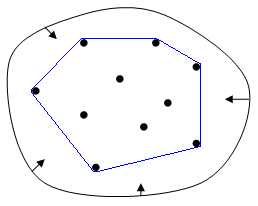
简单来说，可以想象在平面中有一些点，这些点的集合为 \(X\)，我们拿一个橡皮圈撑到最大，尝试套住所有的点，待橡皮圈绷紧后，它会成为一个多边形，这个多边形所有顶点组成的集合便为集合 \(X\) 的凸包。如图：

Gift wrapping 算法

这是我在做 MIT 6.031-Problem Set 0 时，实验指导建议的做法。由于这门课教授的是软件构造，不太注重时间复杂度，所以这个算法时间性能并不好，使用者寥寥，但是它很直观且很有趣，从它开始入门凸包问题不失为一个好的选择

所谓 Gift wrapping，顾名思义，就是模拟包装礼品盒的过程。要拿包装带给一个礼品盒包装，首先肯定是从凸包中的一个点开始，沿着某一条边后到达下一个顶点，然后从包装带原来的方向开始，逐步向内旋转，直到接触到下一个点，那么下一条边就包装完成了。文字描述有些困难，可以看图：

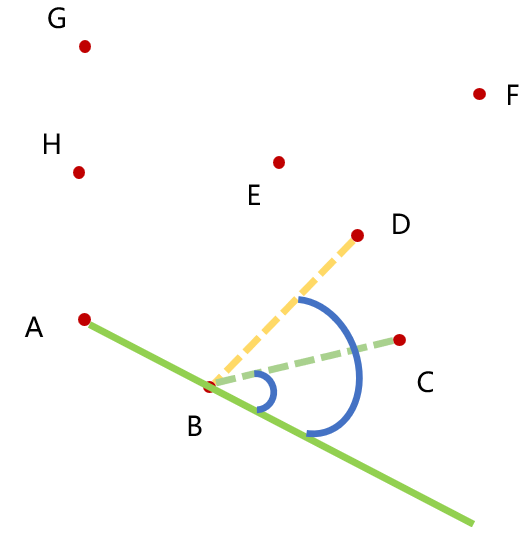
先包装 AB 边，随后包装带从 AB 方向向内旋转，直到遇到 C 点，则凸包的下一个点就是 C

算法：

1.找到一个一定在凸包中的初始点，比如最左下的点
2.计算剩下的所有点与初始点正向下方向之间的角度，取最小的角度的点加入凸包
3.对于最新加入凸包的点，取前一个点指向该点的方向作为初始方向，遍历剩下的点，取剩下的点和该点的连线与初始方向夹角最小的点加入凸包
4.重复 3，直到找到的下一个点是初始点
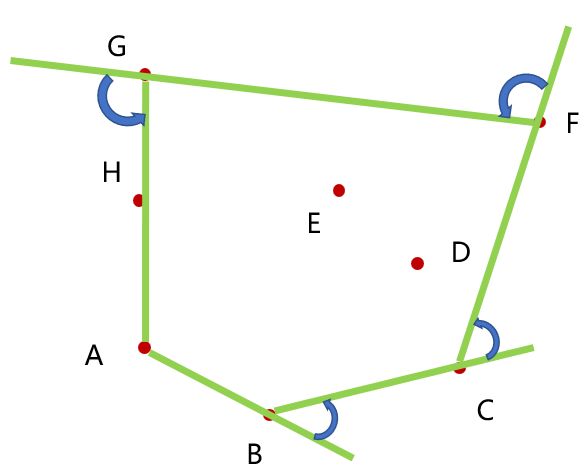
最终结果如图：

计算角度

为了达到目的，先实现一个计算角度的函数，根据初始角度，当前点的坐标，以及目标点的坐标，计算初始角度与当前点和目标点连线的夹角

public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,
                                                 int targetX, int targetY) {
    double angle = 180*Math.atan2(targetY - currentY, targetX - currentX)/Math.PI;
    double bearing;
    bearing = 90 - angle - currentBearing;
    if(bearing < 0) bearing += 360;
    return bearing;
}

这里的角度指的都是从该点正上方逆时针旋转的角度

考虑距离

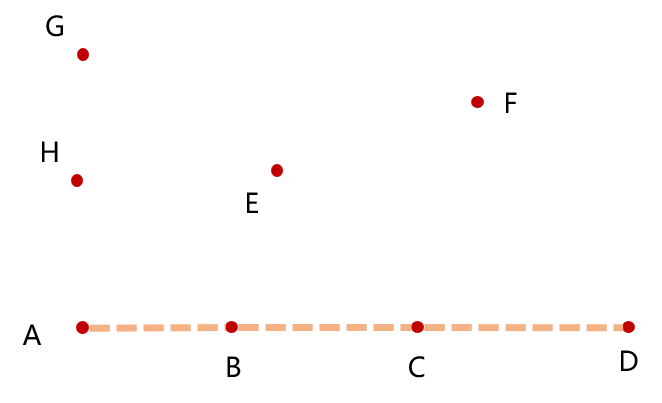
我们先明确一点：对于上图，A、B、C、D 四点共线，由凸包的定义， A、D 应该在凸包中，B，C 不应该在凸包中

从 A 点开始计算角度，角度最小的有 B，C，D 点，那么显然接下来要选择距 A 点最远的 D 点。所有我们的算法在扩充凸包时，应该计算一下距离，如果有多个点需要旋转的角度均最小且相同，则应选择距离最远的点

完整代码

public static Set<Point> convexHull(Set<Point> points) {
    if (points.size() <= 3) return points;
    Set<Point> convexHull = new HashSet<>();


    Point first = points.iterator().next();
    /* 找到最左下边的点，否则如果与起始点同横坐标的点大于等于三，则距离更新的时候，最后永远无法回到起始点 */
    for (Point iter : points) {
	if (iter.x() < first.x() || (iter.x() == first.x() && iter.y() < first.y()))
	    first = iter;
    }
    Point p = first;        //当前的最新点
    /* pre这样设置的目的是使初始角度为0 */
    Point pre = new Point(first.x(), first.y() - 1);      //保存前一个点
    Point endpoint = p;     //待加入集合的点
    do {
	double minAngle = 360;
	double maxDis = 0;
	convexHull.add(p);
	//System.out.println(p.x() + " " + p.y());
	double curBearing = 180 * Math.atan2(p.y() - pre.y(), p.x() - pre.x()) / Math.PI;
	//System.out.println((p.y() - pre.y())+ " " + (p.x() - pre.x()) + ":" + curBearing);
	/* 计算当前角度 */
	if (p.x() >= pre.x()) curBearing = 90 - curBearing;
	else if (p.y() > pre.y()) curBearing = 450 - curBearing;
	else if (p.y() < pre.y()) curBearing = 90 - curBearing;
	//System.out.println(curBearing);
	for (Point next : points) {
		double curAngle = calculateBearingToPoint(curBearing, (int) p.x(), (int) p.y(), (int) next.x(), (int) next.y());
		double curDis = Math.pow(next.x() - p.x(), 2) + Math.pow(next.y() - p.y(), 2);
		/* 要确保这个点与之前的点不同，否则可能会死循环
		   但也要注意可以与第一个点相同，否则循环无法退出 */
		if (curAngle < minAngle && next != p) {
			endpoint = next;
			minAngle = curAngle;
			maxDis = curDis;
		}
		/* 如果有角度相同即共线的，则取最远的点 */
		if (curAngle == minAngle && curDis > maxDis && next != p) {
			maxDis = curDis;
			endpoint = next;
		}
	}
	//System.out.println(minAngle);
	pre = p;
	p = endpoint;
    } while (p != first);
    return convexHull;
}

复杂度分析

对于凸包中的每一个点，都要遍历其它所有点，所以该算法的时间复杂度为 \(O(nh)\)，其中 \(h\) 为凸包中的点数，最坏情况下，所有的点都在凸包中，所以时间复杂度也可以写为 \(O(n^2)\)

由于我这个是按照实验要求写的代码，其中用到了atan，所以时间性能可能会更差。事实上我们不需要精确计算角度，只需要比较角度的大小关系就可以了，可以用点乘来代替角度的计算

Graham 扫描法

先给出算法：

找到一个一定在凸包中的初始点，比如最左下的点
按逆时针逐个加入可能在凸包中的点。做法就是先把剩下的点集按照相对初始点的极角排序，如果极角相同，则按距离排序，近的在前（原因后面解释）
从初始点开始，按顺序不断加入凸包，对于加入的每一个点，判断加入该点后，会不会使凸包呈现一种前一个点往内凹陷的形状，如果是这样的，则从凸包中删除前一个点，继续往前判断（怎么判断形状呢？利用叉乘）
下面我来详细解释一下算法实现

list.sort((a, b) -> {
    /* 按叉乘逆时针 */
	int diff = cross(list.get(0), a, b);
    if (diff == 0) {
    /* 按距离由近到远 */
    	return (distance(list.get(0), a) - distance(list.get(0), b));
    } else {
        return -diff;
    }
});

怎么利用叉乘的性质来判断删除哪些点呢？举如下例子：

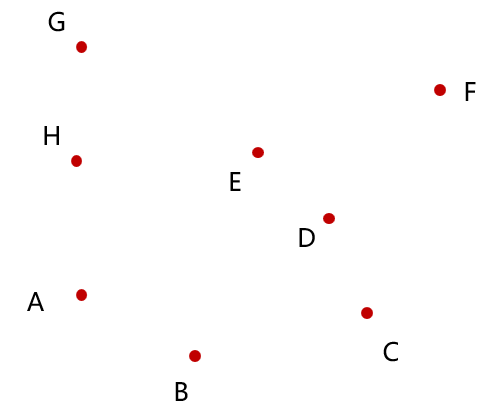
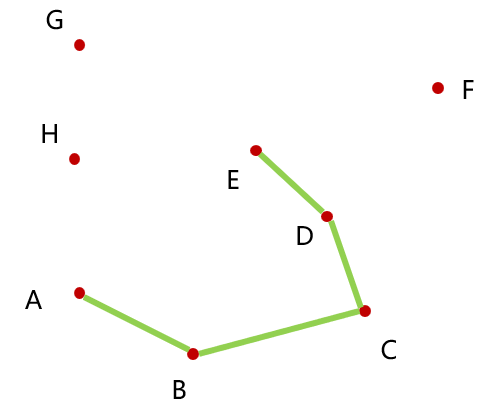
初始点显然是A点，剩下的点按照上述算法描述的排序顺序标号，从 B 点开始不断加入凸包，如图：

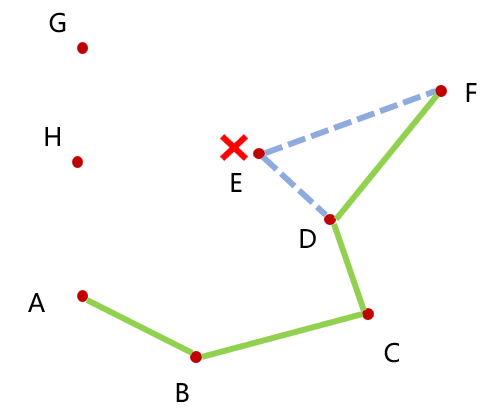
当加入 F 点后，我们要找前两个加入的点来做叉乘，如果 向量DF 相对于 向量 DN 是顺时针的，那么 E 点就会往内凹陷，应该从凸包中删除 E 点

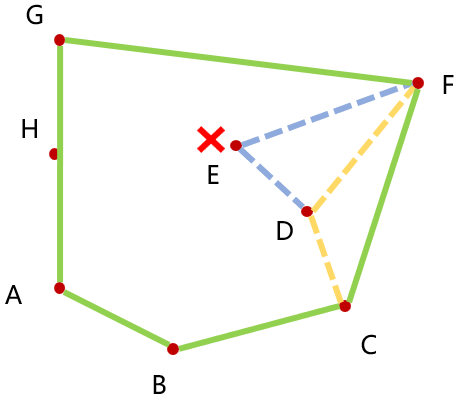
对于加入的每个点，都要与凸包中最近加入的两个点做叉乘运算，很显然，这里可以用栈结构来保存凸包中的点，代码如下：

Deque<Integer> stack = new ArrayDeque<Integer>();
stack.push(0);
stack.push(1);
int n = list.size();
for (int i = 2; i < n; i++) {
    int top = stack.pop();
    /* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线，则弹出栈顶元素 */
    while (!stack.isEmpty() && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
        top = stack.pop();
    }
    stack.push(top);
    stack.push(i);
}

细节：距离判断

为什么对于共线的点，要按它们与初始点的距离从小到大排序呢？

考虑如下例子：

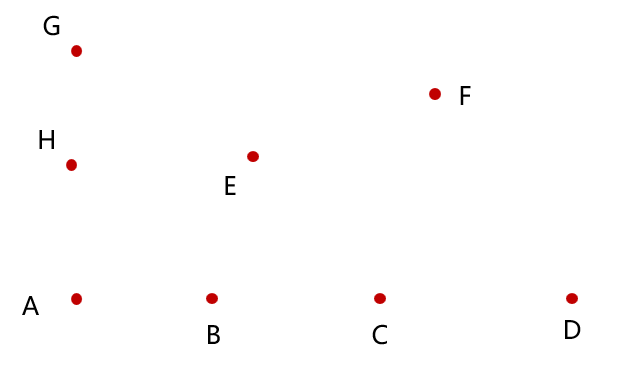
A、B、C、D 四点共线，算法会先加入 A、B 两点，当加入 C 时，AB 与 AC 共线，则会踢掉 B 点，以此类推，最后只会保留 D 点。

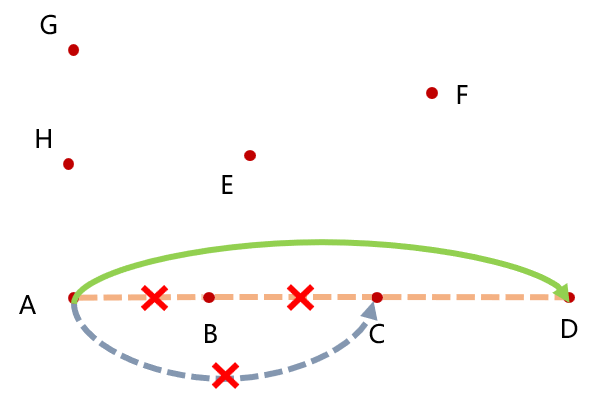
反之，如果不按距离由小到大排序，假如先加入 D 点，则下一步加入 C 点时，算法判断 AC 与 AD 共线，则会踢掉 D 点，那么就会得到错误的答案。

public static Set<Point> convexHull(Set<Point> points) {
    if(points.size() <= 3) return points;
    ArrayList<Point> list = new ArrayList<>(points);
    int first = 0;
    /* 找到最左下的点 */
    for(int i = 0; i < list.size(); i++){
        if(list.get(i).x() < list.get(first).x() || (list.get(i).x() == list.get(first).x() && list.get(i).y() < list.get(first).y()))
            first = i;
    }
    swap(list, first, 0);
    /* 按距离和极角排序 */
    list.sort((a, b) -> {
        int diff = cross(list.get(0), a, b);
        if (diff == 0) {
            return (distance(list.get(0), a) - distance(list.get(0), b));
        } else {
            return -diff;
        }
    });
    Deque<Integer> stack = new ArrayDeque<Integer>();
    /* 将前两个点压入栈中 */
    stack.push(0);
    stack.push(1);
    int n = list.size();
    for (int i = 2; i < n; i++) {
        int top = stack.pop();
        /* 如果当前元素与栈顶的两个元素构成的向量顺时针旋转或共线，则弹出栈顶元素 */
        while (!stack.isEmpty() && cross(list.get(stack.peek()), list.get(top), list.get(i)) <= 0) {
            top = stack.pop();
        }
        stack.push(top);
        stack.push(i);
    }
    Set<Point> ans = new HashSet<>();
    while(!stack.isEmpty()){
        ans.add(list.get(stack.pop()));
    }
    return ans;
}

/* 叉乘 */
public static int cross(Point p, Point q, Point r) {
    return (int)((q.x() - p.x()) * (r.y() - q.y()) - (q.y() - p.y()) * (r.x() - q.x()));
}

/* 求距离 */
public static int distance(Point p, Point q) {
    return (int)((p.x()-q.x())*(p.x()-q.x())+(p.y()-q.y())*(p.y()- q.y()));
}

public static void swap(ArrayList<Point> list, int i, int j) {
    Point temp = list.get(i);
    list.set(i, list.get(j));
    list.set(j, temp);
}

复杂度分析

Andrew 算法

Andrew 算法是 Graham 算法的改进，改进的地方在排序部分。 Graham 算法据极角和距离来进行排序，可能引起较高的时间复杂度，而 Andrew 算法是先对 x 坐标由小到大进行排序，然后对于 x 坐标相等的点再按 y 坐标由小到大排序，对排序时的复杂度有所优化

那么按照什么顺序来更新点呢？Graham 算法的巧妙之处在于通过极角和距离，能让所有点按照逆时针顺序排好序，而 Andrew 算法中按坐标的排序做法就显得有些凌乱了

为了解决这个问题，把凸包的产生分为两部分。排序以后，最左下的点与最右上的点一定在凸包上，并且它们能把凸包分为上凸壳和下凸壳

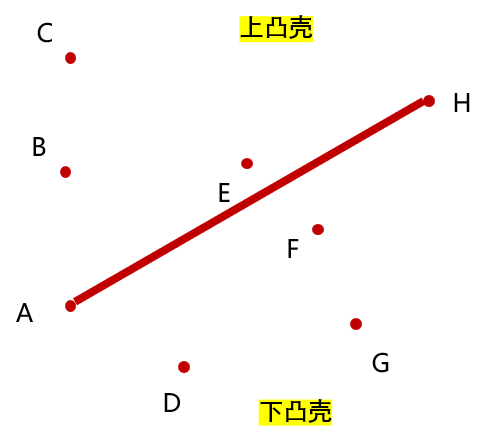
那么对于下凸壳的部分，凸包的点按逆时针是以横坐标从小到大排列的；到达 H 点后，对于上凸壳的部分，凸包的点按逆时针又以横坐标从大到小排列

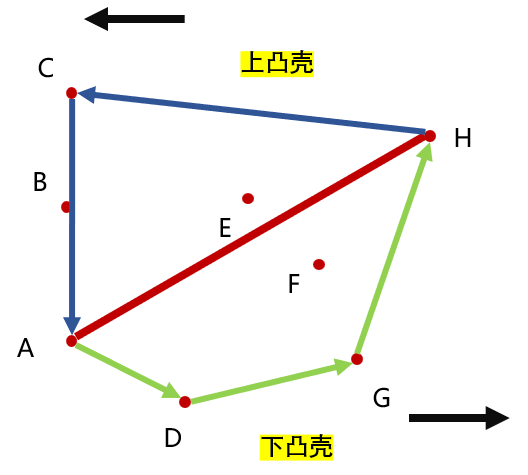
所以排完序后，我们要遍历更新两次，第一轮从正向遍历，得到下凸包部分；第二轮从逆向遍历，得到上凸包部分，更新的做法与 Graham 算法逻辑完全相同

模板 [USACO5.1]圈奶牛Fencing the Cows

#include<bits/stdc++.h>
#define int long long
//#define __int128 int
#define rint register int
using namespace std;
using PII = pair<int,int>;
typedef long long ll;
template<typename T> inline void ckmax(T& x,T y){x=(y>x?y:x); }
template<typename T> inline void ckmin(T& x,T y){x=(y<x?y:x); }
namespace jiasu{
	void inline IOS(){
      ios::sync_with_stdio(false);
	  cin.tie(0);
	  cout.tie(0);
	}
}
using namespace jiasu;
const int maxn = 2e5 + 5;
int n,top,rec,stk[maxn];double ans;
namespace Fast{
    inline int read() {
	    bool flag = false; int x = 0;
	    char ch = getchar();
	    while (ch < '0' || ch > '9') {
	        if (ch == '-') flag = true;
	        ch = getchar();
	    }
	    while (ch >= '0' && ch <= '9') {
	        x=(x << 1) + (x << 3) + ch - '0';
	        ch=getchar();
	    }
	    return flag ? -x : x;
	}
	inline string String_read(){
	    char ch = getchar();
	    string st1 = "";
	    while (!((ch >= 'a') && (ch <= 'z')))
	        ch = getchar();
	    while ((ch >= 'a') && (ch <= 'z'))
	        st1 += ch, ch = getchar();
	    return st1;
	}
	inline double Double_Read(){
	    long long s = 0, w = 1, k = 0, n = 0, m = 0;
	    char ch = getchar();
	    while(ch < '0' || ch > '9'){
	        if(ch == '-') w = -1;
	        ch = getchar();
	    }
	    while((ch >= '0' && ch <= '9') || ch == '.'){
	        if (ch == '.') n = 1;
	        else if (n == 0) s = s * 10 + ch - '0';
	        else k = k * 10 + ch - '0', m++;
	        ch = getchar();
	    }
	    return (pow(0.1, m) * k + s) * w;
	}
    template<typename T> inline void write(T X) {
	    if (X < 0) {putchar('-'); X = ~ (X - 1);}
	    int s[200], top = 0;
	    while (X) {s[++top] = X % 10; X /= 10;}
	    if (!top) s[++top] = 0;
	    while (top) putchar(s[top--] + '0');
	    return;
	}
}
namespace Slove{
	struct vec{double x,y;vec operator-(vec&p)const{return vec{x-p.x,y-p.y};}double len(){return sqrt(x*x+y*y);}}p[maxn];
	double crsprod(vec a,vec b){return a.x*b.y-b.x*a.y;}
	int inline cmp(vec a,vec b){return a.x<b.x||(a.x==b.x&&a.y<b.y); }
}
using namespace Slove;
using namespace Fast;
signed main(void){
	//#ifndef ONLINE_JUDGE
    //freopen("Cows.in","r",stdin);
    //freopen("Cows.out","w",stdout);
    //#endif
    n=read();
	for(rint i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
	sort(p+1,p+1+n,cmp);stk[++top]=1,stk[++top]=2;
	for(rint i=3;i<=n;i++){
		while(top>1&&crsprod(p[stk[top]]-p[stk[top-1]],p[i]-p[stk[top]])<=0.0) top-=1;
		stk[++top]=i;
	}rec=top;
	for(rint i=n-1;i>=1;i--){
		while(top>rec&&crsprod(p[stk[top]]-p[stk[top-1]],p[i]-p[stk[top]])<=0.0) top-=1;
		stk[++top]=i;
	}
	for(rint i=1;i<top;i++) ans+=(p[stk[i+1]]-p[stk[i]]).len();
	printf("%.2lf\n",ans);
	return 0;
	//fclose(stdin);
	//fclose(stdout);
	//fflush(stdout);
}