三分算法

简介

三分法的原理也很简单，和二分法几乎一模一样，只不过我们分隔区间的时候，不是将区间一分为二，而是一分为三。之后，我们同样通过缩小区间的方法来确定要查找的值所在。

看到这里，我相信你们应该都能理解算法原理，但是肯定会有一个问题要问：既然分成两份就能解决问题，我们为什么要分成三份呢？

在回答这个问题之前，我们先来看另一个问题。在数学上，二分法究竟解决了一个什么问题？

还记得二分法使用的前提么？数组必须是有序的，所以二分法其实解决的是单调函数的求解的问题。只要数组是有序的，根据函数的定义就可以看做是一个将数组下标映射到数组取值的函数。显然，这是一个单调函数。我们通过二分法查找其中的一个元素v，本质其实是查找 \(f(x) = v\)

这个函数的解。

所以，二分法使用的场景是单调函数，也就是一次函数。那如果我要搜索二次函数的最小值，用二分法可行吗？

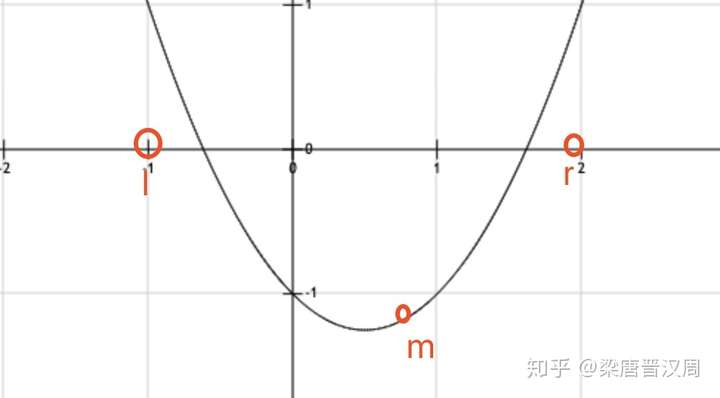
显然不可行，因为我们在取完mid之后， 并不知道答案可能出现在左右哪个区间。

这个时候就需要三分法出场了。

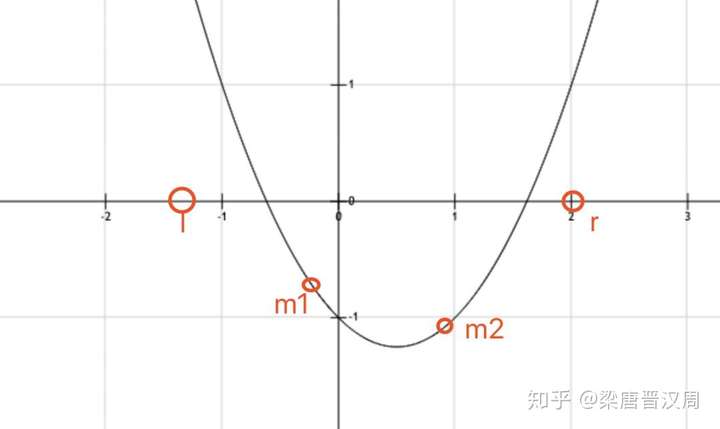
三分法会将区间分成三份，这个我们都已经知道了。分成三份，自然需要两个端点。这两个端点各有一个值，我们分别叫做m1和m2。我们要求的是函数的最小值，所以我们要想极值逼近。

但是我们有两个中间点，该怎么逼近呢？

我们直接根据函数图像来分析，根据上图我们可以看出来，m1和m2的函数值和它们距离极值点的远近是有关系的。离极值点越近，函数值越小(也有可能越大，视函数而定)。在上图当中，\(f(m_2)<f(m_1)\)

所以m2离极值点更近。我们要缩小区间范围，逼近极值点，所以我们应该让 \(l=m_1\)

这里有一点小问题，我们怎么确定极值点在m2和m1中间呢？万一在m2的右侧该怎么办呢？

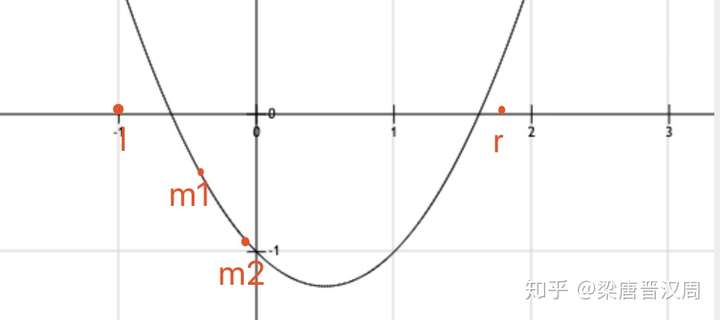
我们画出图像来看，这种情况其实并没有区别，我们只会抛弃区间[l, m1]

，并不会影响极值点。

会不会极值点在m1左侧呢？这是不可能的，因为如果极值点在m1左侧，那么m2距离极值点一定比m1远，这种情况下m2处的函数值是不可能小于m1的。

也就是说，三分法的精髓在于，每次通过比较两个值的大小，缩小三分之一的区间。直到最后区间的范围小于我们设定的阈值为止。算法并不难理解，但是当我们真正碰到二次函数的极值问题的时候，如果没有事先接触过三分法，很难一下想到算法。

三分法本身并不难，我们理解了算法之后，写出伪代码来就很容易了：

def trichotomy():
    l, r = start, end
    epsilon = 1e-6
    # 我们自定义的终止条件是区间长度小于1d-6
    while l + epsilon < r:
        margin = (r - l) / 3.0
        m1 = l + margin
        m2 = m1 + margin
        if f(m1) <= f(m2):
            r = m2
        else:
            l = m1
    return l