启发式合并

一般启发式合并

启发式合并指的是，对于两个集合 x 和 y 合并的操作，每次把元素个数更少的集合合并到元素个数更大的集合内，即：设 x 为元素更少的集合，那么就把 x 合并到 y 内。

可以证明，启发式合并的时间复杂度为：\(O(nlog_n)\)，因为对于每个元素，他所处的集合被合并 k 次，那么这个元素就被合并 k 次，但是每次合并都会使得集合的大小乘以 2，那么一个集合最多被合并 \(log_2n\) 次，所有一个元素最多被合并 \(log_2n\) 次，因此 n 个元素被合并的复杂度为 \(O(nlog_2n)\)

树上启发式合并

强大的解决对于子树的询问问题。
树上启发式合并（dsu on tree）对于某些树上离线问题可以速度大于等于大部分算法且更易于理解和实现的算法。

考虑下面的问题：

给出一棵树，每个节点有颜色，询问一些子树的颜色数量（颜色可重复）。

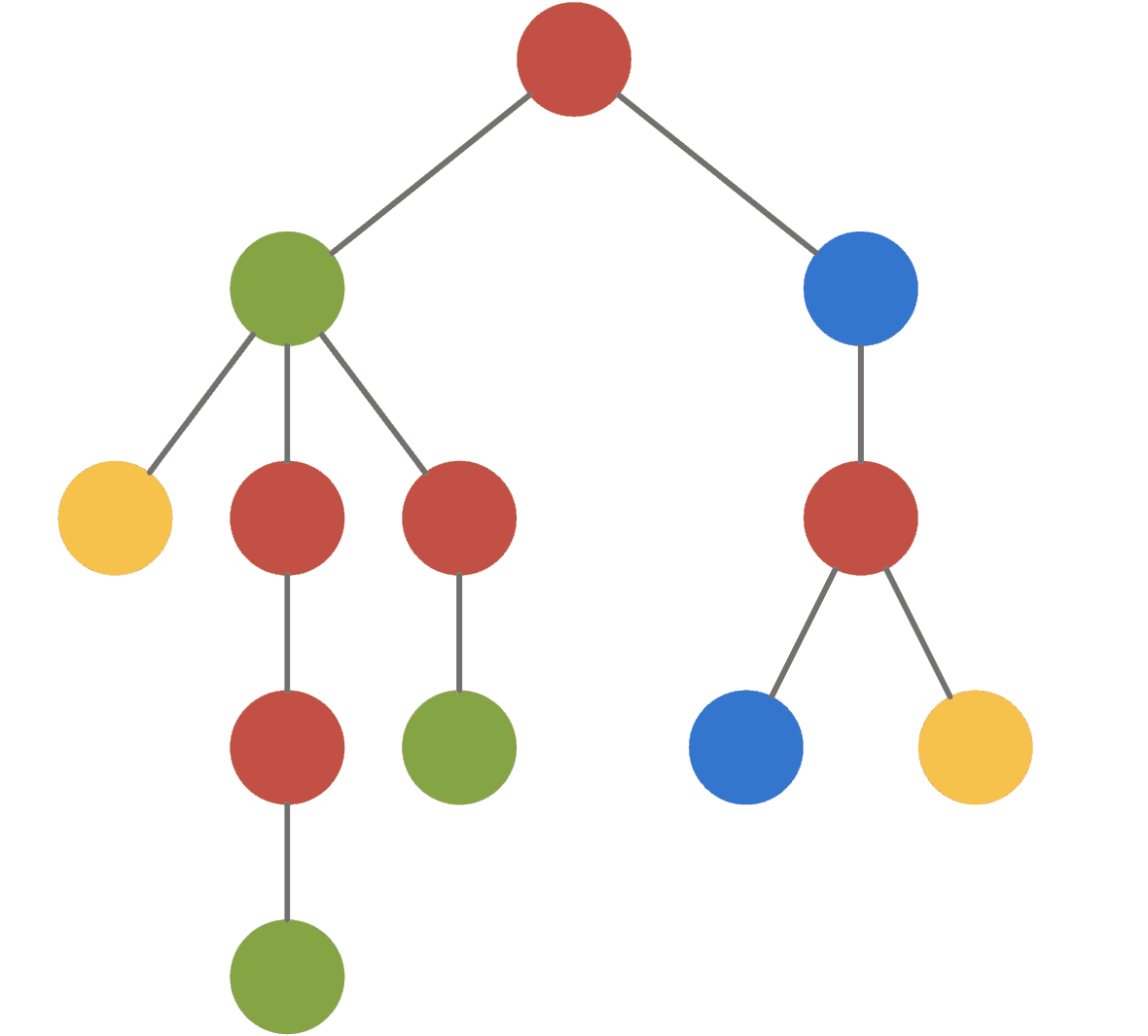
对于每一个节点，我们可以 dfs 向下搜索来计数每个子树内出现次数最多的颜色是哪个，然后 dfs 完就需要再次 dfs 来清空数组，这样是 \(O(n^2)\)。启发式合并是指，我们每次将 dfs 划分为对重儿子 dfs 和轻儿子 dfs ，那么对于父节点u的答案就是两种 dfs 的和。

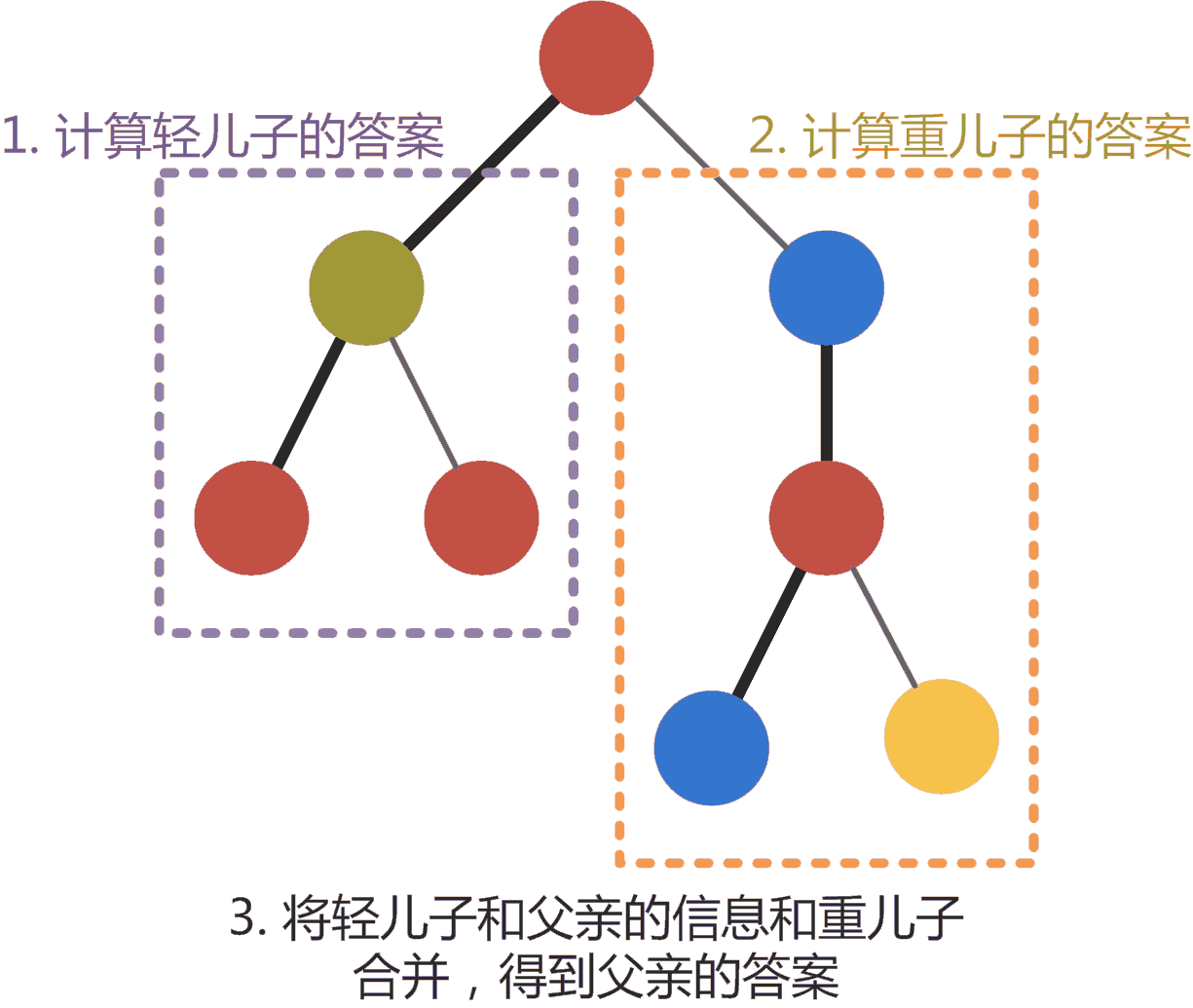
我们每次再做dfs清空的时候不需要清空 u 节点的所有子树，只需要清空所有的轻子树，这样的复杂度为 \(O(nlogn)\)。复杂度证明：对于每个点，其所处的子树被清空一次就会有一次操作，对于一个点来说，最坏的情况就是这个点一直处于轻子树，那就会一直被清空，而轻边最多有 \(O(logn)\) 条，那么一个点最多被清空 \(O(log_n)\) 次，则所有点最多被清空 \(O(nlog_n)\) 次。

模板

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
const int N = 100010, M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int color[N], cnt[N], sz[N], son[N];  // son[u]记录u点的重儿子
LL ans[N], sum;
int mx;

void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }

// 把每个点的重儿子找到
int dfs_son(int u, int father) {
    sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        sz[u] += dfs_son(j, u);
        if (sz[j] > sz[son[u]]) son[u] = j;
    }
    return sz[u];
}

// 计数u为根的子树的主要颜色，但是不计数pson(如果pson != 0说明不计算重儿子，如果=0说明全部都要计算)
// sign表示当前节点对于cnt数组的贡献，sign=1表示当前节点要加到cnt数组，=-1说明要情况当前节点的贡献
void update(int u, int father, int sign, int pson) {
    int c = color[u];  // u节点颜色
    cnt[c] += sign;  // 加上当前节点贡献
    if (cnt[c] > mx)  // 如果大于最大的颜色数目
        mx = cnt[c], sum = c;  // 更新最大的颜色数目，更新最大的颜色权重和
    else if (cnt[c] == mx)  // 如果和最大的颜色数目相等，只要更新最大的颜色权值和
        sum += c;

    for (int i = h[u]; ~i; i = ne[i]) {  // 遍历子树，计算子树的贡献，不计算pson的贡献
        int j = e[i];
        if (j == father || j == pson) continue;
        update(j, u, sign, pson);  // 计数所有轻儿子
    }
}

// 计算u点的主要颜色的和,keep表示当前节点的子树是否留下来，keep=0删，keep=1留
void dfs(int u, int father, int keep) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father || j == son[u]) continue;  // 如果是重儿子，不计算
        dfs(j, u, 0);  // 优先遍历轻儿子，然后清理cnt数组，打上keep=0的标记
    }

    if (son[u]) dfs(son[u], u, 1);  // 搜索重儿子，它的cnt数组不清空，打上keep=1的标记
    update(u, father, 1, son[u]);  // 将cnt数组加上所有除了重儿子之外的贡献(即轻儿子)

    ans[u] = sum;  // 更新u点的出现次数最多的颜色的权值和

    if (!keep) update(u, father, -1, 0), sum = mx = 0;  // 如果当前点的keep标记为0，那么表示要删除当前点的贡献，即cnt数组
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &color[i]);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    dfs_son(1, -1);  // 先把每个点的重儿子找到
    dfs(1, -1, 1);  // 计算主要颜色

    for (int i = 1; i <= n; i++) printf("%lld ", ans[i]);
    return 0;
}