组合计数

简介

组合数学主要是研究某组离散对象满足一定条件的安排的存在性、构造及计数等问题。组合计数理论是组合数学中一个最基本的研究方向，主要研究满足一定条件的安排方式的数目及其计数问题。本课程主要介绍组合数学中常见的和重要的一些计数原理、计数方法和计数公式，包括一般的排列、组合的计算以及生成函数、容斥原理、反演原理、Polya 计数定理等等，是研究组合数学的初步。

常用计算公式

定义

运算

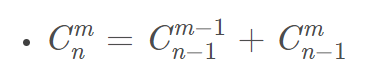
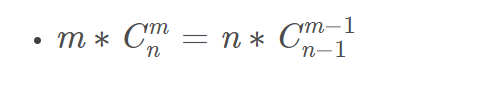
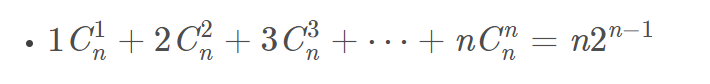
二项式定理

这就是二项式定理，等式右边即为 $(a+b)^n$的二项展开式，它共有 $n+1$ 项
叫做二项展开式的第 $r+1$ 项，也即通项，用 $T_{r+1}$ 表示

叫做第 $r+1$ 项的二项式系数

代码

 
 
//组合数学计算c(n,m)
 
1、c(n,m)=n!/(m!*(n-m)!)
 
long long cal_c(int n, int m)
{
    long long c;
    if(n < m)
        c=0;
    else if (n == m || m == 0)
        c=1;
    else 
	{
        c = 1;
        n = n - m + 1;
        for (int i=1; i<=m; i++) 
		{
            c *= n++;
            c /= i;
        }    
    }
    return c;
}
 
long long cal_c(int n,int k)
{
	if(k>n/2)
	    k=n-k;    //减少枚举量 
	
	long long a=1,b=1;
	for(int i=1;i<=m;i++)
    {
        a*=n+1-i;
        b*=i;
        if(a%b==0)
            a/=b,b=1;
    }
    return a/b; 
}
 
2、数学知识 c(n,m)=c(n-1,m)+c(n-1,m-1)
 
void db()
{
	for(int i=0;i<maxn;i++)
    	    c[i][0]=1;
	for(int i=1;i<maxn;i++)
    	    for(int j=1;j<maxn;j++)
        	c[i][j]=c[i-1][j]+c[i-1][j-1];  	
}