动态规划— —提高Ⅳ
区间DP
一、问题
给定长为n的序列a[i],每次可以将连续一段回文序列消去,消去后左右两边会接到一起,求最少消几次能消完整个序列,n≤500。

f[i][j]表示消去区间[i,j]需要的最少次数。
则
若a[i]=a[j],则还有
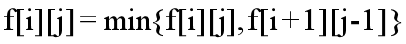
这里实际上是以区间长度为阶段的,这种DP我们通常称为区间DP。
区间DP的做法较为固定,即枚举区间长度,再枚举左端点,之后枚举区间的断点进行转移。
二、概念
区间类型动态规划是线性动态规划的拓展,它在分阶段划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。(例:f[i][j]=f[i][k]+f[k+1][j])
区间类动态规划的特点:
合并:即将两个或多个部分进行整合。
特征:能将问题分解成为两两合并的形式。
求解:对整个问题设最优值,枚举合并点,将问题分解成为左右两个部分,最后将左右两个部分的最优值进行合并得到原问题的最优值。
三.常见解题思路
一、区间DP解题时常见思路
如果题目中答案满足:
-
大的区间的答案可以由小的区间答案组合或加减得到
-
大的范围可以由小的范围代表
-
数据范围较小
我们这时可以考虑采用区间DP来解决。
那么常见的解法有两种:
1.用小的区间组合松弛大的区间,即枚举断点,分割区间,与答案取优。
2.用比当前区间略小的区间转移,用一些区间边界代表转移用的性质,通过常数的加减得到答案。
四.代码实现
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 410, INF = 0x3f3f3f3f;
int n;
int w[N], s[N];
int f[N][N], g[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
{
cin >> w[i];
w[i + n] = w[i];
}
for (int i = 1; i <= n * 2; i ++ ) s[i] = s[i - 1] + w[i];
memset(f, 0x3f, sizeof f);
memset(g, -0x3f, sizeof g);
for (int len = 1; len <= n; len ++ )
for (int l = 1; l + len - 1 <= n * 2; l ++ )
{
int r = l + len - 1;
if (l == r) f[l][r] = g[l][r] = 0;
else
{
for (int k = l; k < r; k ++ )
{
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
}
}
}
int minv = INF, maxv = -INF;
for (int i = 1; i <= n; i ++ )
{
minv = min(minv, f[i][i + n - 1]);
maxv = max(maxv, g[i][i + n - 1]);
}
cout << minv << endl << maxv << endl;
return 0;
}
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m×r×n(Mars 单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕ 表示两颗珠子的聚合操作,(j⊕k) 表示第 j,k 两颗珠子聚合后所释放的能量。则
第 4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000,第 i 个数为第 i 颗珠子的头标记,当 i<N 时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
4≤N≤100,
1≤E≤2.1×10^9
输入样例:
4
2 3 5 10
输出样例:
710
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 210, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ )
{
cin >> w[i];
w[i + n] = w[i];
}
for (int len = 3; len <= n + 1; len ++ )
for (int l = 1; l + len - 1 <= n * 2; l ++ )
{
int r = l + len - 1;
for (int k = l + 1; k < r; k ++ )
f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
}
int res = 0;
for (int l = 1; l <= n; l ++ ) res = max(res, f[l][l + n]);
cout << res << endl;
return 0;
}
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。
每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第 1 行:一个整数 n,为节点个数。
第 2 行:n 个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第 1 行:一个整数,为最高加分(结果不会超过int范围)。
第 2 行:n 个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
n<30
输入样例:
5
5 7 1 2 10
输出样例:
145
3 1 2 4 5
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30;
int n;
int w[N];
int f[N][N], g[N][N];
void dfs(int l, int r)
{
if (l > r) return;
int k = g[l][r];
cout << k << ' ';
dfs(l, k - 1);
dfs(k + 1, r);
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
for (int len = 1; len <= n; len ++ )
for (int l = 1; l + len - 1 <= n; l ++ )
{
int r = l + len - 1;
if (len == 1) f[l][r] = w[l], g[l][r] = l;
else
{
for (int k = l; k <= r; k ++ )
{
int left = k == l ? 1 : f[l][k - 1];
int right = k == r ? 1 : f[k + 1][r];
int score = left * right + w[k];
if (f[l][r] < score)
{
f[l][r] = score;
g[l][r] = k;
}
}
}
}
cout << f[1][n] << endl;
dfs(1, n);
return 0;
}
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N,表示顶点数量。
第二行包含 N 个整数,依次为顶点 1 至顶点 N 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50,
数据保证所有顶点的权值都小于109
输入样例:
5
121 122 123 245 231
输出样例:
12214884
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 55, M = 35, INF = 1e9;
int n;
int w[N];
LL f[N][N][M];
void add(LL a[], LL b[])
{
static LL c[M];
memset(c, 0, sizeof c);
for (int i = 0, t = 0; i < M; i ++ )
{
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
void mul(LL a[], LL b)
{
static LL c[M];
memset(c, 0, sizeof c);
LL t = 0;
for (int i = 0; i < M; i ++ )
{
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
int cmp(LL a[], LL b[])
{
for (int i = M - 1; i >= 0; i -- )
if (a[i] > b[i]) return 1;
else if (a[i] < b[i]) return -1;
return 0;
}
void print(LL a[])
{
int k = M - 1;
while (k && !a[k]) k -- ;
while (k >= 0) cout << a[k -- ];
cout << endl;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
LL temp[M];
for (int len = 3; len <= n; len ++ )
for (int l = 1; l + len - 1 <= n; l ++ )
{
int r = l + len - 1;
f[l][r][M - 1] = 1;
for (int k = l + 1; k < r; k ++ )
{
memset(temp, 0, sizeof temp);
temp[0] = w[l];
mul(temp, w[k]);
mul(temp, w[r]);
add(temp, f[l][k]);
add(temp, f[k][r]);
if (cmp(f[l][r], temp) > 0)
memcpy(f[l][r], temp, sizeof temp);
}
}
print(f[1][n]);
return 0;
}
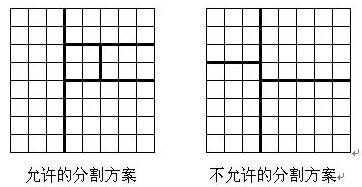
将一个 8×8 的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了 (n−1) 次后,连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n 块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差formula.png ,其中平均值lala.png ,xi 为第 i 块矩形棋盘的总分。
请编程对给出的棋盘及 n,求出均方差的最小值。
输入格式
第 1 行为一个整数 n。
第 2 行至第 9 行每行为 8 个小于 100 的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1<n<15
输入样例:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
输出样例:
1.633
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 15, M = 9;
const double INF = 1e9;
int n, m = 8;
int s[M][M];
double f[M][M][M][M][N];
double X;
int get_sum(int x1, int y1, int x2, int y2)
{
return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}
double get(int x1, int y1, int x2, int y2)
{
double sum = get_sum(x1, y1, x2, y2) - X;
return (double)sum * sum / n;
}
double dp(int x1, int y1, int x2, int y2, int k)
{
double &v = f[x1][y1][x2][y2][k];
if (v >= 0) return v;
if (k == 1) return v = get(x1, y1, x2, y2);
v = INF;
for (int i = x1; i < x2; i ++ )
{
v = min(v, get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));
v = min(v, get(i + 1, y1, x2, y2) + dp(x1, y1, i, y2, k - 1));
}
for (int i = y1; i < y2; i ++ )
{
v = min(v, get(x1, y1, x2, i) + dp(x1, i + 1, x2, y2, k - 1));
v = min(v, get(x1, i + 1, x2, y2) + dp(x1, y1, x2, i, k - 1));
}
return v;
}
int main()
{
cin >> n;
for (int i = 1; i <= m; i ++ )
for (int j = 1; j <= m; j ++ )
{
cin >> s[i][j];
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
X = (double)s[m][m] / n;
memset(f, -1, sizeof f);
printf("%.3lf\n", sqrt(dp(1, 1, 8, 8, n)));
return 0;
}
树形DP
一、概念
1、什么是树型动态规划
树型动态规划就是在“树”的数据结构上的动态规划,平时作的动态规划都是线性的或者是建立在图上的,线性的动态规划有二种方向既向前和向后,相应的线性的动态规划有二种方法既顺推与逆推,而树型动态规划是建立在树上的,所以也相应的有二个方向:
叶->根:在回溯的时候从叶子节点往上更新信息
根 - >叶:往往是在从叶往根dfs一遍之后(相当于预处理),再重新往下获取最后的答案。
不管是 从叶->根 还是 从 根 - >叶,两者都是根据需要采用,没有好坏高低之分。
2、树真的是一种特别特别优美的结构!
用来做动态规划也简直是锦上添花再美不过的事,因为树本身至少就有“子结构”性质(树和子树);本身就具有递归性。所以在树上DP其实是其所当然的事,相比线性动态规划来讲,转移方程更直观,更易理解。
3、难点
和线性动态规划相比,树形DP往往是要利用递归+记忆化搜索。
细节多,较为复杂的树形DP,从子树,从父亲,从兄弟……一些小的要处理的地方,脑子不清晰的时候做起来颇为恶心
状态表示和转移方程,也是真正难的地方。做到后面,树形DP的老套路都也就那么多,难的还是怎么能想出转移方程,各种DP做到最后都是这样!
4.解题规律总结
一般来说树形dp在设状态转移方程时都可以用f[i][]表示i这颗子树怎么怎么样的最优解,实现时一般都是用子树更新父亲(即从下向上更新),那么首先应该考虑的是一个一个子树的更新父亲还是把所有子树都算完了在更新父亲?这就要因题而异了,一般来说有两种情况:
-
1.需要把所有子树的信息都掌握之后再更新子树的就需要把所有子树都算完了在更新父亲。
-
2.而像树上背包这样的问题就需要一个一个的更新,每次都用一个子树更新已经更新完的子树+父亲,最后就可以将这一部分的子树更新完了,再继续往上更新,最后根节点就是答案。
其实上面的两种情况可以总结成一种情况就是一个个子树更新父亲,一般来说第一种情况应用更多,也能解决第二情况的问题,只不过如果符合第二种情况的时候用第二种可以速度更快一点,毕竟你省了一遍循环嘛。
在分题型说说说说树形dp的规律!
子树和计数。
这类问题主要是统计子树和,通过加减一些子树满足题目中要求的某些性质。
树上背包问题
这类问题就是让你求在树上选一些点满足价值最大的问题,一般都可以设f[i][j]表示i这颗子树选j个点的最优解。
花费最少的费用覆盖所有点
这类问题是父亲与孩子有联系的题。基本有两种出法:1.选父亲必须不能选孩子(强制)2.选父亲可以不用选孩子(不强制)。
二.找树的直径小技巧
找树的直径
1.任取一点作为起点,找到距离该点最远的一个点u。(dfs,BFS)
2.再找到距离点u最远的一点v。(dfs,BFS)
那么u和v之间的路径就是这条树的直径
三.代码实现
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, M = N * 2;
int n;
int h[N], e[M], w[M], ne[M], idx;
int ans;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs(int u, int father)
{
int dist = 0; // 表示从当前点往下走的最大长度
int d1 = 0, d2 = 0;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
int d = dfs(j, u) + w[i];
dist = max(dist, d);
if (d >= d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
ans = max(ans, d1 + d2);
return dist;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
return 0;
}
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤105
输入样例:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;
int n;
int h[N], e[M], w[M], ne[M], idx;
int d1[N], d2[N], p1[N], up[N];
bool is_leaf[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs_d(int u, int father)
{
d1[u] = d2[u] = -INF;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
int d = dfs_d(j, u) + w[i];
if (d >= d1[u])
{
d2[u] = d1[u], d1[u] = d;
p1[u] = j;
}
else if (d > d2[u]) d2[u] = d;
}
if (d1[u] == -INF)
{
d1[u] = d2[u] = 0;
is_leaf[u] = true;
}
return d1[u];
}
void dfs_u(int u, int father)
{
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
if (p1[u] == j) up[j] = max(up[u], d2[u]) + w[i];
else up[j] = max(up[u], d1[u]) + w[i];
dfs_u(j, u);
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs_d(1, -1);
dfs_u(1, -1);
int res = d1[1];
for (int i = 2; i <= n; i ++ )
if (is_leaf[i]) res = min(res, up[i]);
else res = min(res, max(d1[i], up[i]));
printf("%d\n", res);
return 0;
}
如果一个数 x 的约数之和 y(不包括他本身)比他本身小,那么 x 可以变成 y,y 也可以变成 x。
例如,4 可以变为 3,1 可以变为 7。
限定所有数字变换在不超过 n 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 n。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
1≤n≤50000
输入样例:
7
输出样例:
3
样例解释
一种方案为:4→3→1→7。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 50010, M = N;
int n;
int h[N], e[M], w[M], ne[M], idx;
int sum[N];
bool st[N];
int ans;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int dfs(int u)
{
st[u] = true;
int dist = 0;
int d1 = 0, d2 = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j])
{
int d = dfs(j);
dist = max(dist, d);
if (d >= d1) d2 = d1, d1 = d;
else if (d > d2) d2 = d;
}
}
ans = max(ans, d1 + d2);
return dist + 1;
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
for (int j = 2; j <= n / i; j ++ )
sum[i * j] += i;
for (int i = 2; i <= n; i ++ )
if (sum[i] < i)
add(sum[i], i);
for (int i = 1; i <= n; i ++ )
if (!st[i])
dfs(i);
cout << ans << endl;
return 0;
}
有一棵二叉苹果树,如果树枝有分叉,一定是分两叉,即没有只有一个儿子的节点。
这棵树共 N 个节点,编号为 1 至 N,树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
这里的保留是指最终与1号点连通。
输入格式
第一行包含两个整数 N 和 Q,分别表示树的节点数以及要保留的树枝数量。
接下来 N−1 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。
输出格式
输出仅一行,表示最多能留住的苹果的数量。
数据范围
1≤Q<N≤100.
N≠1,
每根树枝上苹果不超过 30000 个。
输入样例:
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出样例:
21
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110, M = N * 2;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int f[N][N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{
for (int i = h[u]; ~i; i = ne[i])
{
if (e[i] == father) continue;
dfs(e[i], u);
for (int j = m; j; j -- )
for (int k = 0; k + 1 <= j; k ++ )
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[e[i]][k] + w[i]);
}
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
printf("%d\n", f[1][m]);
return 0;
}
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
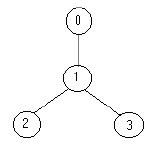
例如,下面的树:
只需要放置 1 名士兵(在节点 1 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 0 到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
0<N≤1500,
一个测试点所有 N 相加之和不超过 300650。
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx;
int f[N][2];
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][0] = 0, f[u][1] = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += f[j][1];
f[u][1] += min(f[j][0], f[j][1]);
}
}
int main()
{
while (cin >> n)
{
memset(h, -1, sizeof h);
idx = 0;
memset(st, 0, sizeof st);
for (int i = 0; i < n; i ++ )
{
int id, cnt;
scanf("%d:(%d)", &id, &cnt);
while (cnt -- )
{
int ver;
cin >> ver;
add(id, ver);
st[ver] = true;
}
}
int root = 0;
while (st[root]) root ++ ;
dfs(root);
printf("%d\n", min(f[root][0], f[root][1]));
}
return 0;
}
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。
第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。
对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
1≤n≤1500
输入样例:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
样例解释:
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1510;
int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][2] = w[u];
int sum = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(min(f[j][0], f[j][1]), f[j][2]);
sum += min(f[j][1], f[j][2]);
}
f[u][1] = 1e9;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
f[u][1] = min(f[u][1], sum - min(f[j][1], f[j][2]) + f[j][2]);
}
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
{
int id, cost, cnt;
cin >> id >> cost >> cnt;
w[id] = cost;
while (cnt -- )
{
int ver;
cin >> ver;
add(id, ver);
st[ver] = true;
}
}
int root = 1;
while (st[root]) root ++ ;
dfs(root);
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}
数位DP
数位dp是一种计数用的dp,一般就是要统计一个区间[le,ri]内满足一些条件数的个数。所谓数位dp,字面意思就是在数位上进行dp咯。数位还算是比较好听的名字,数位的含义:一个数有个位、十位、百位、千位......数的每一位就是数位啦!
之所以要引入数位的概念完全就是为了dp。数位dp的实质就是换一种暴力枚举的方式,使得新的枚举方式满足dp的性质,然后记忆化就可以了。
两种不同的枚举:对于一个求区间[le,ri]满足条件数的个数,最简单的暴力如下:
for(int i=le;i<=ri;i++)
if(right(i)) ans++;
然而这样枚举不方便记忆化,或者说根本无状态可言。
新的枚举:控制上界枚举,从最高位开始往下枚举,例如:ri=213,那么我们从百位开始枚举:百位可能的情况有0,1,2(觉得这里枚举0有问题的继续看)
然后每一位枚举都不能让枚举的这个数超过上界213(下界就是0或者1,这个次要),当百位枚举了1,那么十位枚举就是从0到9,因为百位1已经比上界2小了,后面数位枚举什么都不可能超过上界。所以问题就在于:当高位枚举刚好达到上界是,那么紧接着的一位枚举就有上界限制了。具体的这里如果百位枚举了2,那么十位的枚举情况就是0到1,如果前两位枚举了21,最后一位之是0到3(这一点正好对于代码模板里的一个变量limit 专门用来判断枚举范围)。最后一个问题:最高位枚举0:百位枚举0,相当于此时我枚举的这个数最多是两位数,如果十位继续枚举0,那么我枚举的就是以为数咯,因为我们要枚举的是小于等于ri的所以数,当然不能少了位数比ri小的咯!(这样枚举是为了无遗漏的枚举,不过可能会带来一个问题,就是前导零的问题,模板里用lead变量表示,不过这个不是每个题目都是会有影响的,可能前导零不会影响我们计数,具体要看题目)
由于这种新的枚举只控制了上界所以我们的Main函数总是这样:
int main()
{
long long le,ri;
while(~scanf("%lld%lld",&le,&ri))
printf("%lld\n",solve(ri)-solve(le-1));
}
统计[1,ri]数量和[1,le-1],然后相减就是区间[le,ri]的数量了,这里我写的下界是1,其实0也行,反正相减后就没了,注意题目中le的范围都是大于等于1的(不然le=0,再减一就废了)
一个基本的动态模板(先看后面的例题也行):dp思想,枚举到当前位置pos,状态为state(这个就是根据题目来的,可能很多,毕竟dp千变万化)的数量(既然是计数,dp值显然是保存满足条件数的个数)
typedef long long ll;
int a[20];
ll dp[20][state];//不同题目状态不同
ll dfs(int pos,/*state变量*/,bool lead/*前导零*/,bool limit/*数位上界变量*/)//不是每个题都要判断前导零
{
//递归边界,既然是按位枚举,最低位是0,那么pos==-1说明这个数我枚举完了
if(pos==-1) return 1;/*这里一般返回1,表示你枚举的这个数是合法的,那么这里就需要你在枚举时必须每一位都要满足题目条件,也就是说当前枚举到pos位,一定要保证前面已经枚举的数位是合法的。不过具体题目不同或者写法不同的话不一定要返回1 */
//第二个就是记忆化(在此前可能不同题目还能有一些剪枝)
if(!limit && !lead && dp[pos][state]!=-1) return dp[pos][state];
/*常规写法都是在没有限制的条件记忆化,这里与下面记录状态是对应,具体为什么是有条件的记忆化后面会讲*/
int up=limit?a[pos]:9;//根据limit判断枚举的上界up;这个的例子前面用213讲过了
ll ans=0;
//开始计数
for(int i=0;i<=up;i++)//枚举,然后把不同情况的个数加到ans就可以了
{
if() ...
else if()...
ans+=dfs(pos-1,/*状态转移*/,lead && i==0,limit && i==a[pos]) //最后两个变量传参都是这样写的
/*这里还算比较灵活,不过做几个题就觉得这里也是套路了
大概就是说,我当前数位枚举的数是i,然后根据题目的约束条件分类讨论
去计算不同情况下的个数,还有要根据state变量来保证i的合法性,比如题目
要求数位上不能有62连续出现,那么就是state就是要保存前一位pre,然后分类,
前一位如果是6那么这意味就不能是2,这里一定要保存枚举的这个数是合法*/
}
//计算完,记录状态
if(!limit && !lead) dp[pos][state]=ans;
/*这里对应上面的记忆化,在一定条件下时记录,保证一致性,当然如果约束条件不需要考虑lead,这里就是lead就完全不用考虑了*/
return ans;
}
ll solve(ll x)
{
int pos=0;
while(x)//把数位都分解出来
{
a[pos++]=x%10;//个人老是喜欢编号为[0,pos),看不惯的就按自己习惯来,反正注意数位边界就行
x/=10;
}
return dfs(pos-1/*从最高位开始枚举*/,/*一系列状态 */,true,true);//刚开始最高位都是有限制并且有前导零的,显然比最高位还要高的一位视为0嘛
}
int main()
{
ll le,ri;
while(~scanf("%lld%lld",&le,&ri))
{
//初始化dp数组为-1,这里还有更加优美的优化,后面讲
printf("%lld\n",solve(ri)-solve(le-1));
}
}
常用优化
memset(dp,-1,sizeof dp);放在多组数据外面。
这一点是一个数位特点,使用的条件是:约束条件是每个数自身的属性,而与输入无关。
具体的:上一题不要62和4,这个约束对每一个数都是确定的,就是说任意一个数满不满足这个约束都是确定,比如444这个数,它不满足约束条件,不管你输入的区间是多少你都无法改变这个数不满足约束这个事实,这就是数自身的属性(我们每组数据只是在区间计数而已,只能说你输入的区间不包含444的话,我们就不把它统计在内,而无法改变任何事实)。
由此,我们保存的状态就可以一直用(注意还有要limit,不同区间是会影响数位在有限制条件下的上限的)
这点优化就不给具体题目了,这个还有进一步的扩展。不过说几个我遇到的简单的约束:
-
1.求数位和是10的倍数的个数,这里简化为数位
sum%10这个状态,即dp[pos][sum]这里10 是与多组无关的,所以可以memset优化,不过注意如果题目的模是输入的话那就不能这样了。 -
2.求二进制1的数量与0的数量相等的个数,这个也是数自身的属性。
当然,相减也是个很好的优化方式!!!
代码实现
求给定区间 [X,Y] 中满足下列条件的整数个数:这个数恰好等于 K 个互不相等的 B 的整数次幂之和。
例如,设 X=15,Y=20,K=2,B=2,则有且仅有下列三个数满足题意:
17=24+20
18=24+21
20=24+22
输入格式
第一行包含两个整数 X 和 Y,接下来两行包含整数 K 和 B。
输出格式
只包含一个整数,表示满足条件的数的个数。
数据范围
1≤X≤Y≤231−1,
1≤K≤20,
2≤B≤10
输入样例:
15 20
2
2
输出样例:
3
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 35;
int K, B;
int f[N][N];
void init()
{
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) f[i][j] = 1;
else f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
}
int dp(int n)
{
if (!n) return 0;
vector<int> nums;
while (n) nums.push_back(n % B), n /= B;
int res = 0;
int last = 0;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
if (x) // 求左边分支中的数的个数
{
res += f[i][K - last];
if (x > 1)
{
if (K - last - 1 >= 0) res += f[i][K - last - 1];
break;
}
else
{
last ++ ;
if (last > K) break;
}
}
if (!i && last == K) res ++ ; // 最右侧分支上的方案
}
return res;
}
int main()
{
init();
int l, r;
cin >> l >> r >> K >> B;
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
科协里最近很流行数字游戏。
某人命名了一种不降数,这种数字必须满足从左到右各位数字呈非下降关系,如 123,446。
现在大家决定玩一个游戏,指定一个整数闭区间 [a,b],问这个区间内有多少个不降数。
输入格式
输入包含多组测试数据。
每组数据占一行,包含两个整数 a 和 b。
输出格式
每行给出一组测试数据的答案,即 [a,b] 之间有多少不降数。
数据范围
1≤a≤b≤231−1
输入样例:
1 9
1 19
输出样例:
9
18
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 15;
int f[N][N]; // f[i, j]表示一共有i位,且最高位填j的数的个数
void init()
{
for (int i = 0; i <= 9; i ++ ) f[1][i] = 1;
for (int i = 2; i < N; i ++ )
for (int j = 0; j <= 9; j ++ )
for (int k = j; k <= 9; k ++ )
f[i][j] += f[i - 1][k];
}
int dp(int n)
{
if (!n) return 1;
vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
int res = 0;
int last = 0;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
for (int j = last; j < x; j ++ )
res += f[i + 1][j];
if (x < last) break;
last = x;
if (!i) res ++ ;
}
return res;
}
int main()
{
init();
int l, r;
while (cin >> l >> r) cout << dp(r) - dp(l - 1) << endl;
return 0;
}
Windy 定义了一种 Windy 数:不含前导零且相邻两个数字之差至少为 2 的正整数被称为 Windy 数。
Windy 想知道,在 A 和 B 之间,包括 A 和 B,总共有多少个 Windy 数?
输入格式
共一行,包含两个整数 A 和 B。
输出格式
输出一个整数,表示答案。
数据范围
1≤A≤B≤2×109
输入样例1:
1 10
输出样例1:
9
输入样例2:
25 50
输出样例2:
20
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 11;
int f[N][10];
void init()
{
for (int i = 0; i <= 9; i ++ ) f[1][i] = 1;
for (int i = 2; i < N; i ++ )
for (int j = 0; j <= 9; j ++ )
for (int k = 0; k <= 9; k ++ )
if (abs(j - k) >= 2)
f[i][j] += f[i - 1][k];
}
int dp(int n)
{
if (!n) return 0;
vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
int res = 0;
int last = -2;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
for (int j = i == nums.size() - 1; j < x; j ++ )
if (abs(j - last) >= 2)
res += f[i + 1][j];
if (abs(x - last) >= 2) last = x;
else break;
if (!i) res ++ ;
}
// 特殊处理有前导零的数
for (int i = 1; i < nums.size(); i ++ )
for (int j = 1; j <= 9; j ++ )
res += f[i][j];
return res;
}
int main()
{
init();
int l, r;
cin >> l >> r;
cout << dp(r) - dp(l - 1) << endl;
return 0;
}
由于科协里最近真的很流行数字游戏。
某人又命名了一种取模数,这种数字必须满足各位数字之和 mod N 为 0。
现在大家又要玩游戏了,指定一个整数闭区间 [a.b],问这个区间内有多少个取模数。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含三个整数 a,b,N。
输出格式
对于每个测试数据输出一行结果,表示区间内各位数字和 mod N 为 0 的数的个数。
数据范围
1≤a,b≤231−1,
1≤N<100
输入样例:
1 19 9
输出样例:
2
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 11, M = 110;
int P;
int f[N][10][M];
int mod(int x, int y)
{
return (x % y + y) % y;
}
void init()
{
memset(f, 0, sizeof f);
for (int i = 0; i <= 9; i ++ ) f[1][i][i % P] ++ ;
for (int i = 2; i < N; i ++ )
for (int j = 0; j <= 9; j ++ )
for (int k = 0; k < P; k ++ )
for (int x = 0; x <= 9; x ++ )
f[i][j][k] += f[i - 1][x][mod(k - j, P)];
}
int dp(int n)
{
if (!n) return 1;
vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
int res = 0;
int last = 0;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
for (int j = 0; j < x; j ++ )
res += f[i + 1][j][mod(-last, P)];
last += x;
if (!i && last % P == 0) res ++ ;
}
return res;
}
int main()
{
int l, r;
while (cin >> l >> r >> P)
{
init();
cout << dp(r) - dp(l - 1) << endl;
}
return 0;
}
杭州人称那些傻乎乎粘嗒嗒的人为 62(音:laoer)。
杭州交通管理局经常会扩充一些的士车牌照,新近出来一个好消息,以后上牌照,不再含有不吉利的数字了,这样一来,就可以消除个别的士司机和乘客的心理障碍,更安全地服务大众。
不吉利的数字为所有含有 4 或 62 的号码。例如:62315,73418,88914 都属于不吉利号码。但是,61152 虽然含有 6 和 2,但不是 连号,所以不属于不吉利数字之列。
你的任务是,对于每次给出的一个牌照号区间 [n,m],推断出交管局今后又要实际上给多少辆新的士车上牌照了。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含一个整数对 n 和 m。
当输入一行为“0 0”时,表示输入结束。
输出格式
对于每个整数对,输出一个不含有不吉利数字的统计个数,该数值占一行位置。
数据范围
1≤n≤m≤109
输入样例:
1 100
0 0
输出样例:
80
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 35;
int f[N][10];
void init()
{
for (int i = 0; i <= 9; i ++ )
if (i != 4)
f[1][i] = 1;
for (int i = 1; i < N; i ++ )
for (int j = 0; j <= 9; j ++ )
{
if (j == 4) continue;
for (int k = 0; k <= 9; k ++ )
{
if (k == 4 || j == 6 && k == 2) continue;
f[i][j] += f[i - 1][k];
}
}
}
int dp(int n)
{
if (!n) return 1;
vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
int res = 0;
int last = 0;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
for (int j = 0; j < x; j ++ )
{
if (j == 4 || last == 6 && j == 2) continue;
res += f[i + 1][j];
}
if (x == 4 || last == 6 && x == 2) break;
last = x;
if (!i) res ++ ;
}
return res;
}
int main()
{
init();
int l, r;
while (cin >> l >> r, l || r)
{
cout << dp(r) - dp(l - 1) << endl;
}
return 0;
}
单身!
依然单身!
吉哥依然单身!
DS 级码农吉哥依然单身!
所以,他平生最恨情人节,不管是 214 还是 77,他都讨厌!
吉哥观察了 214 和 77 这两个数,发现:
2+1+4=7
7+7=7×2
77=7×11
最终,他发现原来这一切归根到底都是因为和 7 有关!
所以,他现在甚至讨厌一切和 7 有关的数!
什么样的数和 7 有关呢?
如果一个整数符合下面三个条件之一,那么我们就说这个整数和 7 有关:
整数中某一位是 7;
整数的每一位加起来的和是 7 的整数倍;
这个整数是 7 的整数倍。
现在问题来了:吉哥想知道在一定区间内和 7 无关的整数的平方和。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据占一行,包含两个整数 L 和 R。
输出格式
对于每组数据,请计算 [L,R] 中和 7 无关的数字的平方和,并将结果对 109+7 取模后输出。
数据范围
1≤T≤50,
1≤L≤R≤1018
输入样例:
3
1 9
10 11
17 17
输出样例:
236
221
0
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 20, P = 1e9 + 7;
struct F
{
int s0, s1, s2;
}f[N][10][7][7];
int power7[N], power9[N];
int mod(LL x, int y)
{
return (x % y + y) % y;
}
void init()
{
for (int i = 0; i <= 9; i ++ )
{
if (i == 7) continue;
auto& v = f[1][i][i % 7][i % 7];
v.s0 ++, v.s1 += i, v.s2 += i * i;
}
LL power = 10;
for (int i = 2; i < N; i ++, power *= 10)
for (int j = 0; j <= 9; j ++ )
{
if (j == 7) continue;
for (int a = 0; a < 7; a ++ )
for (int b = 0; b < 7; b ++ )
for (int k = 0; k <= 9; k ++ )
{
if (k == 7) continue;
auto &v1 = f[i][j][a][b], &v2 = f[i - 1][k][mod(a - j * power, 7)][mod(b - j, 7)];
v1.s0 = mod(v1.s0 + v2.s0, P);
v1.s1 = mod(v1.s1 + v2.s1 + j * (power % P) % P * v2.s0, P);
v1.s2 = mod(v1.s2 + j * j * (power % P) % P * (power % P) % P * v2.s0 + v2.s2 + 2 * j * power % P * v2.s1, P);
}
}
power7[0] = 1;
for (int i = 1; i < N; i ++ ) power7[i] = power7[i - 1] * 10 % 7;
power9[0] = 1;
for (int i = 1; i < N; i ++ ) power9[i] = power9[i - 1] * 10ll % P;
}
F get(int i, int j, int a, int b)
{
int s0 = 0, s1 = 0, s2 = 0;
for (int x = 0; x < 7; x ++ )
for (int y = 0; y < 7; y ++ )
if (x != a && y != b)
{
auto v = f[i][j][x][y];
s0 = (s0 + v.s0) % P;
s1 = (s1 + v.s1) % P;
s2 = (s2 + v.s2) % P;
}
return {s0, s1, s2};
}
int dp(LL n)
{
if (!n) return 0;
LL backup_n = n % P;
vector<int> nums;
while (n) nums.push_back(n % 10), n /= 10;
int res = 0;
LL last_a = 0, last_b = 0;
for (int i = nums.size() - 1; i >= 0; i -- )
{
int x = nums[i];
for (int j = 0; j < x; j ++ )
{
if (j == 7) continue;
int a = mod(-last_a * power7[i + 1], 7);
int b = mod(-last_b, 7);
auto v = get(i + 1, j, a, b);
res = mod(
res +
(last_a % P) * (last_a % P) % P * power9[i + 1] % P * power9[i + 1] % P * v.s0 % P +
v.s2 +
2 * last_a % P * power9[i + 1] % P * v.s1,
P);
}
if (x == 7) break;
last_a = last_a * 10 + x;
last_b += x;
if (!i && last_a % 7 && last_b % 7) res = (res + backup_n * backup_n) % P;
}
return res;
}
int main()
{
int T;
cin >> T;
init();
while (T -- )
{
LL l, r;
cin >> l >> r;
cout << mod(dp(r) - dp(l - 1), P) << endl;
}
return 0;
}
本文作者:PassName
本文链接:https://www.cnblogs.com/spaceswalker/p/15884839.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】凌霞软件回馈社区,携手博客园推出1Panel与Halo联合会员
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· C#高性能开发之类型系统:从 C# 7.0 到 C# 14 的类型系统演进全景
· 管理100个小程序-很难吗
· 基于Blazor实现的运输信息管理系统
· 如何统计不同电话号码的个数?—位图法
· 微信支付功能的设计实现与关键实践(UniApp+Java)全代码