动态规划——提高Ⅲ
状态机模型
我们知道,一般编写程序时都要画出流程图,按照流程图结构来编程,如果编写一个比较繁琐,容易思维混乱的程序时,我们可以利用有限状态机模型画出一个状态转移图,这样便可以利用画出的逻辑图来编写程序,简洁且不易出错。
那什么是有限状态机是什么意思呢?百度百科上这样解释:
有限状态机,(英语:Finite-state machine, FSM),又称有限状态自动机,简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。
没错,上面的东西肯定没几个人能看懂(用y总的话说叫这个翻译有点蛋疼),所以画个图(还是百度复制的)。
可能还是有些难懂,那就来几道详解例题:
例1.大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T 组数据。
接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。
第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数量。
每家店铺中的现金数量均不超过1000。
输出格式
对于每组数据,输出一行。
该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
数据范围
1≤T≤50,
1≤N≤105
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24
样例解释
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。
我们还是,用闫氏DP法操作。
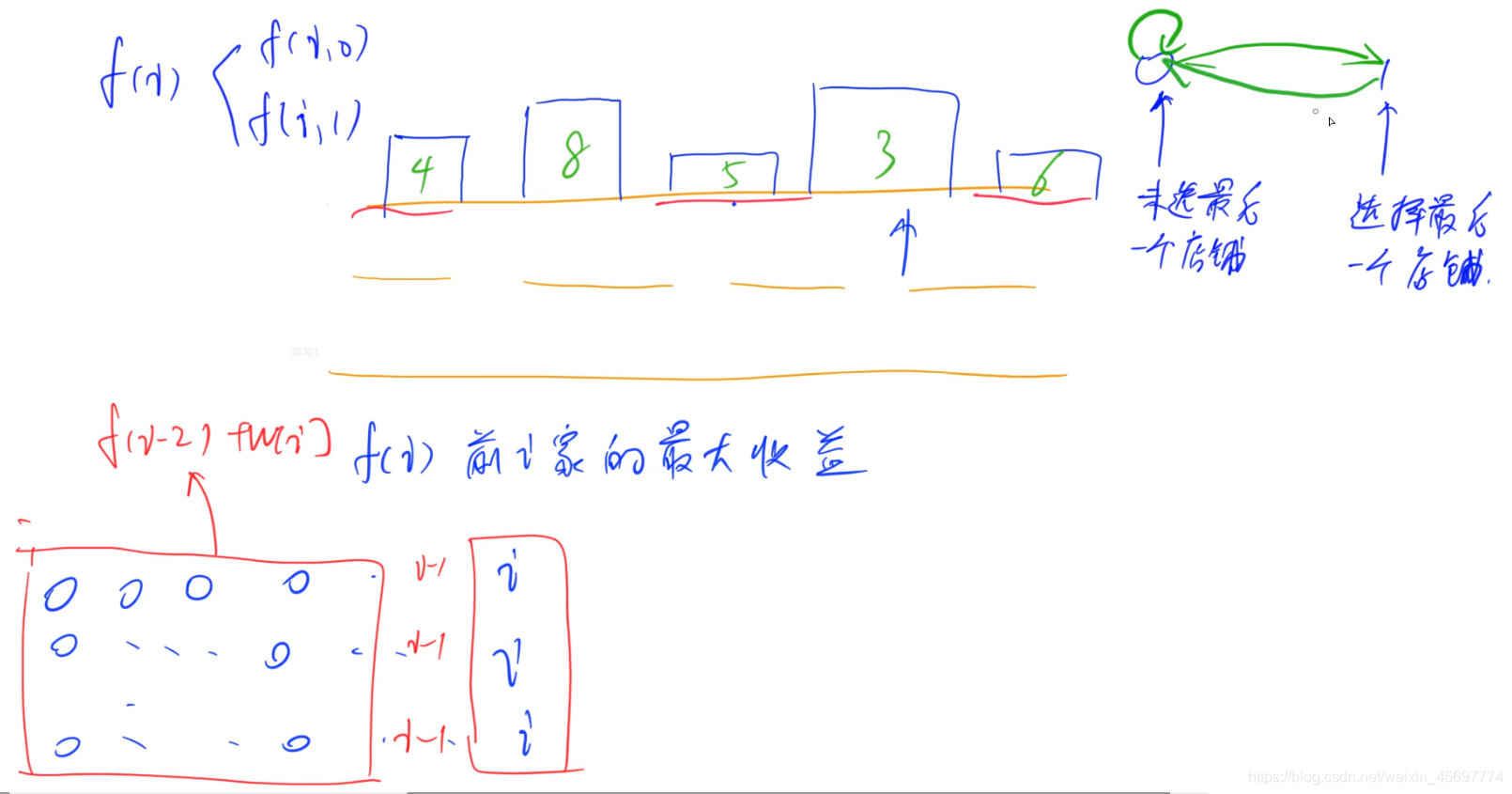
所谓的状态机,可以默认为搜索的方向数组,加到了动态规划上面.(个人理解)
我们发现,这道题目一共就两种状态.
-
不打劫
-
打劫
既然状态已经罗列好了,接下来就是状态之间的转移.
①考虑,当前不打劫,能否转移到下一个不打劫.
可以,因为这个商铺不打劫,那么下一个商铺当然也可以不打劫.
②考虑,当前不打劫,能否转移到下一个打劫.
可以,因为这个商铺没有打劫,那么下一个商铺打劫,不违反相邻两个商铺不能都打劫.
③考虑,当前打劫,能否转移到下一个不打劫.
可以,虽然当前商铺打劫,但是下一个商铺不打劫,所以满足题意.
④考虑,当前打劫,能否转移到下一个打劫.
不可以 ,因为两个相邻的商铺不能同时都打劫.
对于状态机而言,如果上一个状态合法,而且可以转移到当前状态,那么这个转移合法.
个人理解:状态机的转移类似于图论里的添边,如果这条边合理,就引入这条边,状态机的选定类似于状态分类,走哪些种类的路达到最后的目的地.
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int w[N], f[N][2];
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
for (int i = 1; i <= n; i ++ )
{
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + w[i];
}
printf("%d\n", max(f[n][0], f[n][1]));
}
return 0;
}
例2.股票买卖
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润,你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。
输入格式
第一行包含整数 N 和 k,表示数组的长度以及你可以完成的最大交易数量。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105,
1≤k≤100
输入样例1:
3 2
2 4 1
输出样例1:
2
输入样例2:
6 2
3 2 6 5 0 3
输出样例2:
7
样例解释
样例1:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
样例2:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.
画出状态机模型
这里由于题目要求只能进行k次交易,所以我们设置一个二维数组

然后辅以闫氏DP分析法

注意边界的设置:
-
初始化为0->该状态合法,最开始可以从这里转移过来
-
初始化为
-INF/INF表示不希望用到它,最开始不能从它转移过来
代码实现
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 110, INF = 0x3f3f3f3f;
int n, m;
int w[N];
int f[N][M][2];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
memset(f, -0x3f, sizeof f);
for (int i = 0; i <= n; i ++ ) f[i][0][0] = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
}
int res = 0;
for (int i = 0; i <= m; i ++ ) res = max(res, f[n][i][0]);
printf("%d\n", res);
return 0;
}
股票买卖升级版
给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
输入格式
第一行包含整数 N,表示数组长度。
第二行包含 N 个不超过 10000 的正整数,表示完整的数组。
输出格式
输出一个整数,表示最大利润。
数据范围
1≤N≤105
输入样例:
5
1 2 3 0 2
输出样例:
3
样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出],第一笔交易可得利润 2-1 = 1,第二笔交易可得利润 2-0 = 2,共得利润 1+2 = 3。
由于买完股票之后有一天的冷冻期, 所以我们把手里没股票根据题意拆成两种情况,然后分析所有的点与边。

初始化:我们最开始只能从手里无股票两天及以上的这一种情况出发,因为只有这一种可以开始拓展并且符合题意。注意我们必须初始化 f[0][2] = 0; f[0][0] = f[0][1] = -INF;,因为第一次购买股票是要花钱的,如果不将边界设置为-INF,由于取max操作会导致一直不买。
最后答案在f[n][1],f[n][2],f[n][1],f[n][2],f[n][1],f[n][2]之中取最大值,因为有可能股票一直下跌不买为最优,这样2就不会转移到1,出口就不再1了。
代码实现
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][3];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
f[0][0] = f[0][1] = -INF, f[0][2] = 0;
for (int i = 1; i <= n; i ++ )
{
f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
f[i][1] = f[i - 1][0] + w[i];
f[i][2] = max(f[i - 1][2], f[i - 1][1]);
}
printf("%d\n", max(f[n][1], f[n][2]));
return 0;
}
设计密码
你现在需要设计一个密码 S,S 需要满足:
S 的长度是 N;
S 只包含小写英文字母;
S 不包含子串 T;
例如:abc 和 abcde 是 abcde 的子串,abd 不是 abcde 的子串。
请问共有多少种不同的密码满足要求?
由于答案会非常大,请输出答案模 109+7 的余数。
输入格式
第一行输入整数N,表示密码的长度。
第二行输入字符串T,T中只包含小写字母。
输出格式
输出一个正整数,表示总方案数模 109+7 后的结果。
数据范围
1≤N≤50,
1≤|T|≤N,|T|是T的长度。
输入样例1:
2
a
输出样例1:
625
输入样例2:
4
cbc
输出样例2:
456924
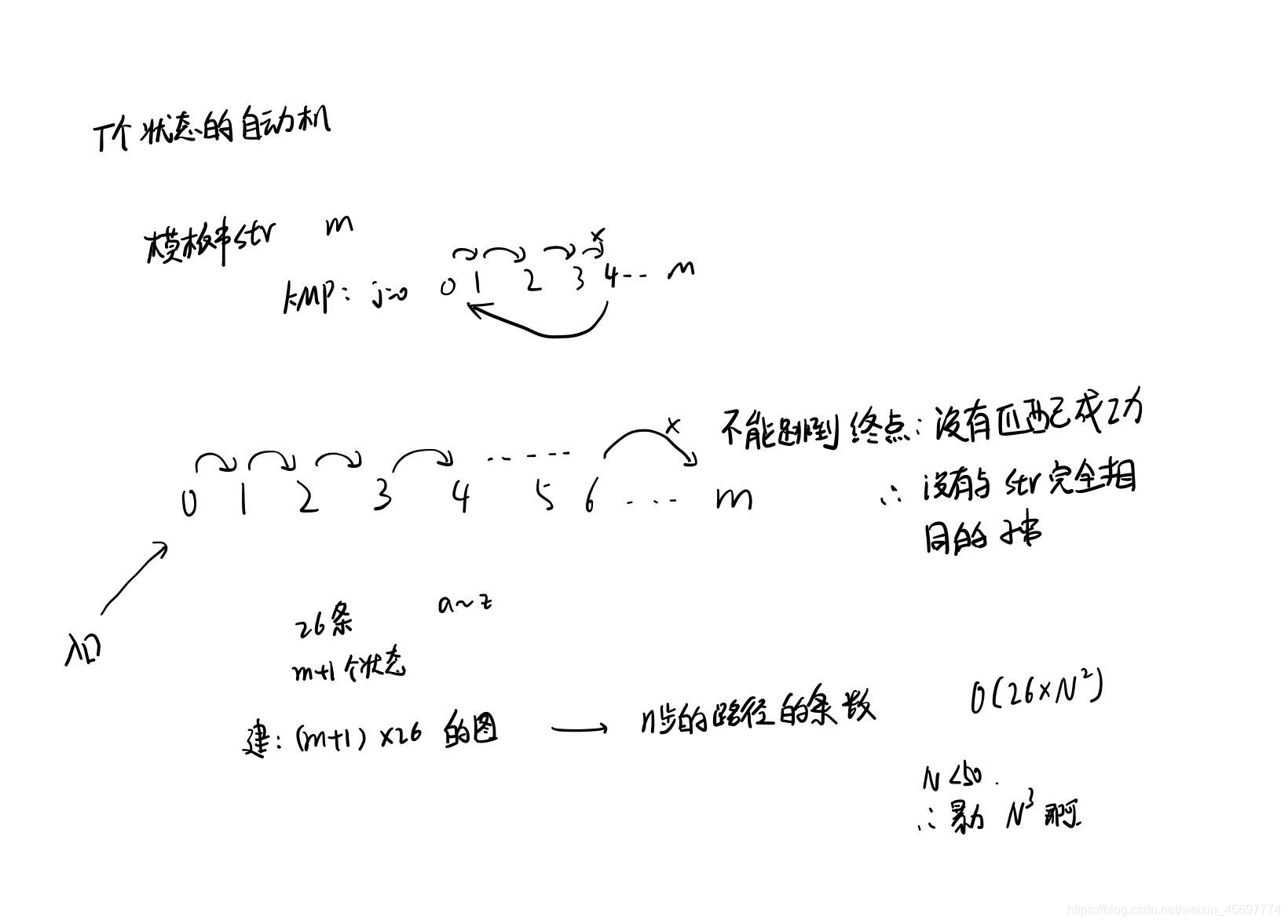
枚举j表示在子串中匹配的状态。
f[i][j]表示我们构造的密码的长度为i,当前需要构造的密码为第i+1位,密码在子串中匹配到了第j位的方案数
如果曾经有一个构造的字符串匹配到了第10位,那么f[i][10] 就会被更新,就不是0,然后枚举到10的时候我们就可以加起来表示由之前匹配到第10位的那一种情况转移过来的。
代码实现
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55, mod = 1e9 + 7;
int n, m;
char str[N];
int nxt[N];
int f[N][N];
int main()
{
cin >> n >> str + 1;
m = strlen(str + 1);
for (int i = 2, j = 0; i <= m; i ++ )
{
while (j && str[i] != str[j + 1]) j = nxt[j];
if (str[i] == str[j + 1]) j ++ ;
nxt[i] = j;
}
f[0][0] = 1;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
for (char k = 'a'; k <= 'z'; k ++ )
{
int u = j;
while (u && k != str[u + 1]) u = nxt[u];
if (k == str[u + 1]) u ++ ;
if (u < m) f[i + 1][u] = (f[i + 1][u] + f[i][j]) % mod;
}
int res = 0;
for (int i = 0; i < m; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
return 0;
}
修复DNA
生物学家终于发明了修复DNA的技术,能够将包含各种遗传疾病的DNA片段进行修复。
为了简单起见,DNA看作是一个由’A’, ‘G’ , ‘C’ , ‘T’构成的字符串。
修复技术就是通过改变字符串中的一些字符,从而消除字符串中包含的致病片段。
例如,我们可以通过改变两个字符,将DNA片段”AAGCAG”变为”AGGCAC”,从而使得DNA片段中不再包含致病片段”AAG”,”AGC”,”CAG”,以达到修复该DNA片段的目的。
需注意,被修复的DNA片段中,仍然只能包含字符’A’, ‘G’ , ‘C’ , ‘T’。
请你帮助生物学家修复给定的DNA片段,并且修复过程中改变的字符数量要尽可能的少。
输入格式
输入包含多组测试数据。
每组数据第一行包含整数N,表示致病DNA片段的数量。
接下来N行,每行包含一个长度不超过20的非空字符串,字符串中仅包含字符’A’, ‘G’ , ‘C’ , ‘T’,用以表示致病DNA片段。
再一行,包含一个长度不超过1000的非空字符串,字符串中仅包含字符’A’, ‘G’ , ‘C’ , ‘T’,用以表示待修复DNA片段。
最后一组测试数据后面跟一行,包含一个0,表示输入结束。
输出格式
每组数据输出一个结果,每个结果占一行。
输入形如”Case x: y”,其中x为测试数据编号(从1开始),y为修复过程中所需改变的字符数量的最小值,如果无法修复给定DNA片段,则y为”-1”。
数据范围
1≤N≤50
输入样例:
2
AAA
AAG
AAAG
2
A
TG
TGAATG
4
A
G
C
T
AGT
0
输出样例:
Case 1: 1
Case 2: 4
Case 3: -1
假设已经修改好了i ii位,在修改第i + 1 i+1i+1位的时候,进行状态转移。
-
状态表示:
f[i][j]表示 长度为 i 的DNA片段,在Trie图当中的状态为 j 的最小操作数. -
状态计算:
f[i+1][p]=min(f[i+1][p],f[i][j+k]==str[i+1])(k∈(A,G,C,T)
代码实现
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int tr[N][4], dar[N], idx;
int q[N], ne[N];
char str[N];
int f[N][N];
int get(char c)
{
if (c == 'A') return 0;
if (c == 'T') return 1;
if (c == 'G') return 2;
return 3;
}
void insert()
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int t = get(str[i]);
if (tr[p][t] == 0) tr[p][t] = ++ idx;
p = tr[p][t];
}
dar[p] = 1;
}
void build()
{
int hh = 0, tt = -1;
for (int i = 0; i < 4; i ++ )
if (tr[0][i])
q[ ++ tt] = tr[0][i];
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = 0; i < 4; i ++ )
{
int p = tr[t][i];
if (!p) tr[t][i] = tr[ne[t]][i];
else
{
ne[p] = tr[ne[t]][i];
q[ ++ tt] = p;
dar[p] |= dar[ne[p]];
}
}
}
}
int main()
{
int T = 1;
while (scanf("%d", &n), n)
{
memset(tr, 0, sizeof tr);
memset(dar, 0, sizeof dar);
memset(ne, 0, sizeof ne);
idx = 0;
for (int i = 0; i < n; i ++ )
{
scanf("%s", str);
insert();
}
build();
scanf("%s", str + 1);
m = strlen(str + 1);
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for (int i = 0; i < m; i ++ )
for (int j = 0; j <= idx; j ++ )
for (int k = 0; k < 4; k ++ )
{
int t = get(str[i + 1]) != k;
int p = tr[j][k];
if (!dar[p]) f[i + 1][p] = min(f[i + 1][p], f[i][j] + t);
}
int res = 0x3f3f3f3f;
for (int i = 0; i <= idx; i ++ ) res = min(res, f[m][i]);
if (res == 0x3f3f3f3f) res = -1;
printf("Case %d: %d\n", T ++, res);
}
return 0;
}
总结:闫氏DP分析法牛逼!!!
状态压缩DP
状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式
很多棋盘问题都运用到了状压,同时,状压也很经常和BFS及DP连用,例题里会给出介绍
有了状态,DP就比较容易了
举个例子:有一个大小为n*n的农田,我们可以在任意处种田,现在来描述一下某一行的某种状态:
设n = 9;
有二进制数 100011011(九位),每一位表示该农田是否被占用,1表示用了,0表示没用,这样一种状态就被我们表示出来了:见下表
| 列数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 二进制 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 是否用 | √ | × | × | × | √ | √ | × | √ | √ |
所以我们最多只需要 \(2^{n+1}-1\) 的十进制数就好(左边那个数的二进制形式是n个1)
现在我们有了表示状态的方法,但心里也会有些不安:上面用十进制表示二进制的数,枚举了全部的状态,DP起来复杂度岂不是很大?没错,状压其实是一种很暴力的算法,因为他需要遍历每个状态,所以将会出现2^n的情况数量,不过这并不代表这种方法不适用:一些题目可以依照题意,排除不合法的方案,使一行的总方案数大大减少从而减少枚举.
接下来还要用到位运算,关于位运算算法我会在后续的博客进行详细解释,如果想初步了解见动态规划初步
例题
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 n 和 k。
输出格式
共一行,表示方案总数,若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n2
输入样例:
3 2
输出样例:
16
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 12, M = 1 << 10, K = 110;
int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
LL f[N][K][M];
bool check(int state)
{
for (int i = 0; i < n; i ++ )
if ((state >> i & 1) && (state >> i + 1 & 1))
return false;
return true;
}
int count(int state)
{
int res = 0;
for (int i = 0; i < n; i ++ ) res += state >> i & 1;
return res;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < 1 << n; i ++ )
if (check(i))
{
state.push_back(i);
cnt[i] = count(i);
}
for (int i = 0; i < state.size(); i ++ )
for (int j = 0; j < state.size(); j ++ )
{
int a = state[i], b = state[j];
if ((a & b) == 0 && check(a | b))
head[i].push_back(j);
}
f[0][0][0] = 1;
for (int i = 1; i <= n + 1; i ++ )
for (int j = 0; j <= m; j ++ )
for (int a = 0; a < state.size(); a ++ )
for (int b : head[a])
{
int c = cnt[state[a]];
if (j >= c)
f[i][j][a] += f[i - 1][j - c][b];
}
cout << f[n + 1][m][0] << endl;
return 0;
}
农夫约翰的土地由 M×N 个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
输入格式
第 1 行包含两个整数 M 和 N。
第 2..M+1 行:每行包含 N 个整数 0 或 1,用来描述整个土地的状况,1 表示该块土地肥沃,0 表示该块土地不育。
输出格式
输出总种植方法对 108 取模后的值。
数据范围
1≤M,N≤12
输入样例:
2 3
1 1 1
0 1 0
输出样例:
9
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
bool check(int state)
{
for (int i = 0; i + 1 < m; i ++ )
if ((state >> i & 1) && (state >> i + 1 & 1))
return false;
return true;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < m; j ++ )
{
int t;
cin >> t;
w[i] += !t * (1 << j);
}
for (int i = 0; i < 1 << m; i ++ )
if (check(i))
state.push_back(i);
for (int i = 0; i < state.size(); i ++ )
for (int j = 0; j < state.size(); j ++ )
{
int a = state[i], b = state[j];
if (!(a & b))
head[i].push_back(j);
}
f[0][0] = 1;
for (int i = 1; i <= n + 1; i ++ )
for (int j = 0; j < state.size(); j ++ )
if (!(state[j] & w[i]))
for (int k : head[j])
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
cout << f[n + 1][0] << endl;
return 0;
}
司令部的将军们打算在 N×M 的网格地图上部署他们的炮兵部队。
一个 N×M 的地图由 N 行 M 列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P 表示),如下图。
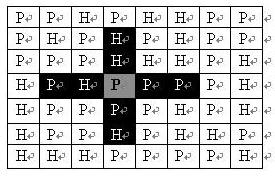
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。
从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 N 和 M;
接下来的 N 行,每一行含有连续的 M 个字符(P 或者 H),中间没有空格。按顺序表示地图中每一行的数据。
输出格式
仅一行,包含一个整数 K,表示最多能摆放的炮兵部队的数量。
数据范围
N≤100,M≤10
输入样例:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例:
6
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 10, M = 1 << 10;
int n, m;
int g[1010];
int f[2][M][M];
vector<int> state;
int cnt[M];
bool check(int state)
{
for (int i = 0; i < m; i ++ )
if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1)))
return false;
return true;
}
int count(int state)
{
int res = 0;
for (int i = 0; i < m; i ++ )
if (state >> i & 1)
res ++ ;
return res;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < m; j ++ )
{
char c;
cin >> c;
g[i] += (c == 'H') << j;
}
for (int i = 0; i < 1 << m; i ++ )
if (check(i))
{
state.push_back(i);
cnt[i] = count(i);
}
for (int i = 1; i <= n; i ++ )
for (int j = 0; j < state.size(); j ++ )
for (int k = 0; k < state.size(); k ++ )
for (int u = 0; u < state.size(); u ++ )
{
int a = state[j], b = state[k], c = state[u];
if (a & b | a & c | b & c) continue;
if (g[i] & b | g[i - 1] & a) continue;
f[i & 1][j][k] = max(f[i & 1][j][k], f[i - 1 & 1][u][j] + cnt[b]);
}
int res = 0;
for (int i = 0; i < state.size(); i ++ )
for (int j = 0; j < state.size(); j ++ )
res = max(res, f[n & 1][i][j]);
cout << res << endl;
return 0;
}
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟, 小鸟们的飞行轨迹均为形如 y=ax2+bx 的曲线,其中 a,b 是 Kiana 指定的参数,且必须满足 a<0。
当小鸟落回地面(即 x 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 n 只绿色的小猪,其中第 i 只小猪所在的坐标为 (xi,yi)。
如果某只小鸟的飞行轨迹经过了 (xi, yi),那么第 i 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 (xi, yi),那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3) 和 (3,3),Kiana 可以选择发射一只飞行轨迹为 y=−x2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana 来说都很难,所以 Kiana 还输入了一些神秘的指令,使得自己能更轻松地完成这个这个游戏。
这些指令将在输入格式中详述。
假设这款游戏一共有 T 个关卡,现在 Kiana 想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。
由于她不会算,所以希望由你告诉她。
注意:本题除 NOIP 原数据外,还包含加强数据。
输入格式
第一行包含一个正整数 T,表示游戏的关卡总数。
下面依次输入这 T 个关卡的信息。
每个关卡第一行包含两个非负整数 n,m,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。
接下来的 n 行中,第 i 行包含两个正实数 (xi,yi),表示第 i 只小猪坐标为 (xi,yi),数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0,表示 Kiana 输入了一个没有任何作用的指令。
如果 m=1,则这个关卡将会满足:至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。
保证 1≤n≤18,0≤m≤2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整,例如 :⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
数据范围
凑活别太小就行
输入样例:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出样例:
1
1
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 18, M = 1 << 18;
const double eps = 1e-8;
int n, m;
PDD q[N];
int path[N][N];
int f[M];
int cmp(double x, double y)
{
if (fabs(x - y) < eps) return 0;
if (x < y) return -1;
return 1;
}
int main()
{
int T;
cin >> T;
while (T -- )
{
cin >> n >> m;
for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
memset(path, 0, sizeof path);
for (int i = 0; i < n; i ++ )
{
path[i][i] = 1 << i;
for (int j = 0; j < n; j ++ )
{
double x1 = q[i].x, y1 = q[i].y;
double x2 = q[j].x, y2 = q[j].y;
if (!cmp(x1, x2)) continue;
double a = (y1 / x1 - y2 / x2) / (x1 - x2);
double b = y1 / x1 - a * x1;
if (cmp(a, 0) >= 0) continue;
int state = 0;
for (int k = 0; k < n; k ++ )
{
double x = q[k].x, y = q[k].y;
if (!cmp(a * x * x + b * x, y)) state += 1 << k;
}
path[i][j] = state;
}
}
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 0; i + 1 < 1 << n; i ++ )
{
int x = 0;
for (int j = 0; j < n; j ++ )
if (!(i >> j & 1))
{
x = j;
break;
}
for (int j = 0; j < n; j ++ )
f[i | path[x][j]] = min(f[i | path[x][j]], f[i] + 1);
}
cout << f[(1 << n) - 1] << endl;
}
return 0;
}
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 n 个深埋在地下的宝藏屋,也给出了这 n 个宝藏屋之间可供开发的 m 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。
但是,每个宝藏屋距离地面都很远,也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。
已经开凿出的道路可以任意通行不消耗代价。
每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。
另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是:
这条道路的长度 × 从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋)。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代价最小,并输出这个最小值。
输入格式
第一行两个用空格分离的正整数 n 和 m,代表宝藏屋的个数和道路数。
接下来 m 行,每行三个用空格分离的正整数,分别是由一条道路连接的两个宝藏屋的编号(编号为 1∼n),和这条道路的长度 v。
输出格式
输出共一行,一个正整数,表示最小的总代价。
数据范围
1≤n≤12,
0≤m≤1000,
v≤5∗105
输入样例:
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
输出样例:
4
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 12, M = 1 << 12, INF = 0x3f3f3f3f;
int n, m;
int d[N][N];
int f[M][N], g[M];
int main()
{
scanf("%d%d", &n, &m);
memset(d, 0x3f, sizeof d);
for (int i = 0; i < n; i ++ ) d[i][i] = 0;
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
a --, b --;
d[a][b] = d[b][a] = min(d[a][b], c);
}
for (int i = 1; i < 1 << n; i ++ )
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
for (int k = 0; k < n; k ++ )
if (d[j][k] != INF)
g[i] |= 1 << k;
}
memset(f, 0x3f, sizeof f);
for (int i = 0; i < n; i ++ ) f[1 << i][0] = 0;
for (int i = 1; i < 1 << n; i ++ )
for (int j = (i - 1); j; j = (j - 1) & i)
if ((g[j] & i) == i)
{
int remain = i ^ j;
int cost = 0;
for (int k = 0; k < n; k ++ )
if (remain >> k & 1)
{
int t = INF;
for (int u = 0; u < n; u ++ )
if (j >> u & 1)
t = min(t, d[k][u]);
cost += t;
}
for (int k = 1; k < n; k ++ ) f[i][k] = min(f[i][k], f[j][k - 1] + cost * k);
}
int res = INF;
for (int i = 0; i < n; i ++ ) res = min(res, f[(1 << n) - 1][i]);
printf("%d\n", res);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号