贪心算法（进阶）
前言
很多人觉得贪心算法就是个基础算法，十分的简单，实际上想真正学好贪心是很难的。y总说过，贪心的不确定性让贪心的难度超越了图论和动态规划。接下来这些贪心的内容可能会颠覆你的世界观（AcWing的同学可以划走了）。
区间问题
区间问题是贪心算法的一个小版块，一个看似简单实际恶心的玩意。它的方法就是做题。
给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，
使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 N，表示区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两
个端点。
输出格式
输出一个整数，表示所需的点的最小数量。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10^9
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);
sort(range, range + n);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ )
if (range[i].l > ed)
{
res ++ ;
ed = range[i].r;
}
printf("%d\n", res);
return 0;
}
给定 N 个闭区间 [ai,bi]，请你在数轴上选择若干区间，使
得选中的区间之间互不相交（包括端点）。
输出可选取区间的最大数量。
输入格式
第一行包含整数 N，表示区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两
个端点。
输出格式
输出一个整数，表示可选取区间的最大数量。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10^9
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);
sort(range, range + n);
int res = 0, ed = -2e9;
for (int i = 0; i < n; i ++ )
if (ed < range[i].l)
{
res ++ ;
ed = range[i].r;
}
printf("%d\n", res);
return 0;
}
给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使
得每组内部的区间两两之间（包括端点）没有交集，并使得组
数尽可能小。
输出最小组数。
输入格式
第一行包含整数 N，表示区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两
个端点。
输出格式
输出一个整数，表示最小组数。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10^9
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return l < W.l;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
priority_queue<int, vector<int>, greater<int>> heap;
for (int i = 0; i < n; i ++ )
{
auto r = range[i];
if (heap.empty() || heap.top() >= r.l) heap.push(r.r);
else
{
heap.pop();
heap.push(r.r);
}
}
printf("%d\n", heap.size());
return 0;
}
给定 N 个闭区间 [ai,bi] 以及一个线段区间 [s,t]，请你选
择尽量少的区间，将指定线段区间完全覆盖。
输出最少区间数，如果无法完全覆盖则输出 −1。
输入格式
第一行包含两个整数 s 和 t，表示给定线段区间的两个端点
。
第二行包含整数 N，表示给定区间数。
接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两
个端点。
输出格式
输出一个整数，表示所需最少区间数。
如果无解，则输出 −1。
数据范围
1≤N≤10^5,
−10^9≤ai≤bi≤10^9,
−10^9≤s≤t≤10^9
输入样例：
1 5
3
-1 3
2 4
3 5
输出样例：
2
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W)const
{
return l < W.l;
}
}range[N];
int main()
{
int st, ed;
scanf("%d%d", &st, &ed);
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i ++ )
{
int j = i, r = -2e9;
while (j < n && range[j].l <= st)
{
r = max(r, range[j].r);
j ++ ;
}
if (r < st)
{
res = -1;
break;
}
res ++ ;
if (r >= ed)
{
success = true;
break;
}
st = r;
i = j - 1;
}
if (!success) res = -1;
printf("%d\n", res);
return 0;
}
Huffman树
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。
目的：
找出存放一串字符所需的最少的二进制编码
构造方法：
首先统计出每种字符出现的频率！（也可以是概率）//权值
构建方式
对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：
-
在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
-
在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；
-
重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。
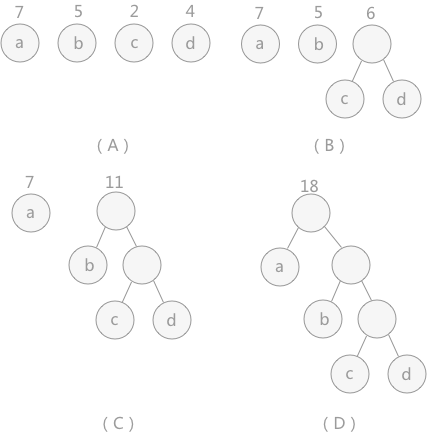
图 中，（A）给定了四个结点a，b，c，d，权值分别为7，5，2，4；第一步如（B）所示，找出现有权值中最小的两个，2 和 4 ，相应的结点 c 和 d 构建一个新的二叉树，树根的权值为 2 + 4 = 6，同时将原有权值中的 2 和 4 删掉，将新的权值 6 加入；进入（C），重复之前的步骤。直到（D）中，所有的结点构建成了一个全新的二叉树，这就是哈夫曼树。
在一个果园里，达达已经将所有的果子打了下来，而且按果子
的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并，达达可以把两堆果子合并到一起，消耗的体力等
于两堆果子的重量之和。
可以看出，所有的果子经过 n−1 次合并之后，就只剩下一堆
了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之
和。
因为还要花大力气把这些果子搬回家，所以达达在合并果子时
要尽可能地节省体力。
假定每个果子重量都为 1，并且已知果子的种类数和每种果子
的数目，你的任务是设计出合并的次序方案，使达达耗费的体
力最少，并输出这个最小的体力耗费值。
例如有 3 种果子，数目依次为 1，2，9。
可以先将 1、2 堆合并，新堆数目为 3，耗费体力为 3。
接着，将新堆与原先的第三堆合并，又得到新的堆，数目为
12，耗费体力为 12。
所以达达总共耗费体力=3+12=15。
可以证明 15 为最小的体力耗费值。
输入格式
输入包括两行，第一行是一个整数 n，表示果子的种类数。
第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i
种果子的数目。
输出格式
输出包括一行，这一行只包含一个整数，也就是最小的体力耗
费值。
输入数据保证这个值小于 231。
数据范围
1≤n≤10000,
1≤ai≤20000
输入样例：
3
1 2 9
输出样例：
15
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
priority_queue<int, vector<int>, greater<int>> heap;
while (n -- )
{
int x;
scanf("%d", &x);
heap.push(x);
}
int res = 0;
while (heap.size() > 1)
{
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
res += a + b;
heap.push(a + b);
}
printf("%d\n", res);
return 0;
}
加强代码：
#include <cstdio>
#include <queue>
#define int long long
using namespace std;
queue <int> q1;
queue <int> q2;
int to[100005];
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
signed main() {
int n;
read(n);
for (int i = 1; i <= n; ++i) {
int a;
read(a);
to[a] ++;
}
for (int i = 1; i <= 100000; ++i) {
while(to[i]) {
to[i] --;
q1.push(i);
}
}
int ans = 0;
for (int i = 1; i < n; ++i) {
int x , y;
if((q1.front() < q2.front() && !q1.empty()) || q2.empty()) {
x = q1.front();
q1.pop();
}
else {
x = q2.front();
q2.pop();
}
if((q1.front() < q2.front() && !q1.empty()) || q2.empty()) {
y = q1.front();
q1.pop();
}
else {
y = q2.front();
q2.pop();
}
ans += x + y;
q2.push(x + y);
}
printf("%lld" , ans);
return 0;
}
排序不等式
1.什么是排序不等式？
大数乘大数加上小数乘小数，大于大数乘小数加小数乘大数，这就叫排序不等式。
当有两组数字Xn和Yn，我们按从小到大分别排序如下：
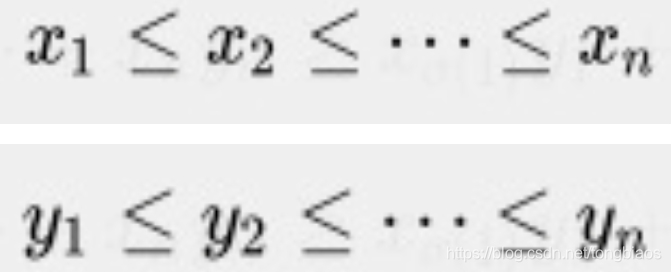
那么有如下结论：
简单说就是按照从小到大的“顺序”相乘的和最大；按照相反顺序，也就是“逆序”相乘的和最小；混乱顺序则处于二者之间。
2.资源配置的“零阶道理”
排序不等式，是资源配置的“零阶道理”。是最底层的“不平等关系”。而正是因为这个逻辑，“效率”和“公平”本质上是矛盾的。
有 n 个人排队到 1 个水龙头处打水，第 i 个人装满水桶所
需的时间是 ti，请问如何安排他们的打水顺序才能使所有人
的等待时间之和最小？
输入格式
第一行包含整数 n。
第二行包含 n 个整数，其中第 i 个整数表示第 i 个人装满
水桶所花费的时间 ti。
输出格式
输出一个整数，表示最小的等待时间之和。
数据范围
1≤n≤10^5,
1≤ti≤10^4
输入样例：
7
3 6 1 4 2 5 7
输出样例：
56
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010;
int n;
int t[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &t[i]);
sort(t, t + n);
reverse(t, t + n);
LL res = 0;
for (int i = 0; i < n; i ++ ) res += t[i] * i;
printf("%lld\n", res);
return 0;
}
绝对值不等式
在不等式应用中，经常涉及质量、面积、体积等，也涉及某些数学对象（如实数、向量）的大小或绝对值。它们都是通过非负数来度量的。
公式：||a|-|b|| ≤|a±b|≤|a|+|b|
在一条数轴上有 N 家商店，它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商
店都要运送一车商品。
为了提高效率，求把货仓建在何处，可以使得货仓到每家商店
的距离之和最小。
输入格式
第一行输入整数 N。
第二行 N 个整数 A1∼AN。
输出格式
输出一个整数，表示距离之和的最小值。
数据范围
1≤N≤100000,
0≤Ai≤40000
输入样例：
4
6 2 9 1
输出样例：
12
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int q[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
sort(q, q + n);
int res = 0;
for (int i = 0; i < n; i ++ ) res += abs(q[i] - q[n / 2]);
printf("%d\n", res);
return 0;
}
推公式
农民约翰的 N 头奶牛（编号为 1..N）计划逃跑并加入马戏
团，为此它们决定练习表演杂技。
奶牛们不是非常有创意，只提出了一个杂技表演：
叠罗汉，表演时，奶牛们站在彼此的身上，形成一个高高的垂
直堆叠。
奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。
这 N 头奶牛中的每一头都有着自己的重量 Wi 以及自己的强
壮程度 Si。
一头牛支撑不住的可能性取决于它头上所有牛的总重量（不包
括它自己）减去它的身体强壮程度的值，现在称该数值为风险
值，风险值越大，这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序，使得所有奶牛的风险值中的最大
值尽可能的小。
输入格式
第一行输入整数 N，表示奶牛数量。
接下来 N 行，每行输入两个整数，表示牛的重量和强壮程
度，第 i 行表示第 i 头牛的重量 Wi 以及它的强壮程度
Si。
输出格式
输出一个整数，表示最大风险值的最小可能值。
数据范围
1≤N≤50000,
1≤Wi≤10,000,
1≤Si≤1,000,000,000
输入样例：
3
10 3
2 5
3 3
输出样例：
2
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 50010;
int n;
PII cow[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int s, w;
scanf("%d%d", &w, &s);
cow[i] = {w + s, w};
}
sort(cow, cow + n);
int res = -2e9, sum = 0;
for (int i = 0; i < n; i ++ )
{
int s = cow[i].first - cow[i].second, w = cow[i].second;
res = max(res, sum - s);
sum += w;
}
printf("%d\n", res);
return 0;
}
