基础数学数论问题
质数和约数
这个章节没啥说的,就是几个函数。
bool is_prime(int x)//判断质数函数
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
void divide(int x)//分解质因数函数
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}
inline int get_primes(int n)//计算1到n之间质数个数
{
int cnt=0;
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue;
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
return cnt;
}
vector<int> get_divisors(int x)//计算x的约数
{
vector<int> res;
int j=0;
for(int i=1;i<=x/i;i++)
if(x%i==0){
res.push_back(i);
if(i!=x/i) res.push_back(x/i);
}
sort(res.begin(),res.end());
return res;//存放进了res数组,输出方式如下
/*
vector<int>::iterator it;
for(it=res.begin();it!=res.end();it++)
cout<<*it<<" ";
*/
//等价于for(auto x : res) cout<<x<< ' ';
}
long long solve(long long n)//计算n的约数总个数
{
long long prime[100100];
bool IsPrime[100100];
long long num;
num=0;
memset(IsPrime,false,sizeof(IsPrime));
for(long long i=2;i<=100000;i++){
if(IsPrime[i]) continue;
prime[num++]=i;
for(long long j=i+i;j<=100000;j+=i)
IsPrime[j]=true;
}
long long ans=1,sum;
for(int i=0;i<num&&prime[i]*prime[i]<=n;i++)
{
long long tmp=prime[i];
sum=0;
if(n%tmp==0)
{
while(n%tmp==0)
{
n/=tmp;
sum++;
}
ans*=(sum+1LL);
}
}
if(n>1) ans*=2;
return ans;
}
埃氏筛
埃拉托色尼筛选法(the Sieve of Eratosthenes)简称埃氏筛法,是古希腊数学家埃拉托色尼(Eratosthenes 274B.C.~194B.C.)提出的一种筛选法。 是针对自然数列中的自然数而实施的,用于求一定范围内的质数,它的容斥原理之完备性条件是 \(p=H~\)。
代码样例
#include <iostream>
using namespace std;
void FilterPrime(int n){
bool* isPrimes = new bool[n+1];
for(int i=2;i<=n;++i)
isPrimes[i] = true;
isPrimes[2] = true;
for(int j=2;j<=n;++j)
if(isPrimes[j]==true)
for(int m=2;j*m<=n;++m)
isPrimes[j*m] = false;
for(int k=2;k<=n;++k)
if(isPrimes[k]==true)
cout<<k<<"是素数"<<endl;
delete [] isPrimes;
}
int main(){
int num;
cin>>num;
FilterPrime(num);
system("pause");
return 0;
}
欧拉筛
欧拉筛法是用线性时间求取给定范围内的素数的个数,当然素数的值也是可以记录的,适用于大范围性的素数求取,如果只是判断某一个素数,欧拉筛就显得大材小用了(费空间资源),这时候可以考虑Miller-Rabin 素数测试。
欧拉函数的时间复杂度趋于O(N)的,即使是1e8也不在话下
讲解欧拉筛之前回顾一下埃拉托斯特尼筛法
埃拉托斯特尼筛法:原理就是先找出一个素数然后把这个素数的倍数都标记为合数(一个正整数的所有倍数一定是合数,除了1),在下一次遇到被标记的数时直接跳过。
例如:
第一次遍历遇到素数2,所以(4,6,8,10…)被标记为合数
第二次遍历遇到素数3,所以(9,12,15…)被标记为合数
第三次遍历遇到合数4,因为已经被2的倍数标记所以直接跳过。
然后按照上面方法一直遍历到最后就筛选出了所有素数。
#include <cstring>
using namespace std;
int prime[1100000],primesize,phi[11000000];
bool isprime[11000000];
void getlist(int listsize)
{
memset(isprime,1,sizeof(isprime));
isprime[1]=false;
for(int i=2;i<=listsize;i++)
{
if(isprime[i])prime[++primesize]=i;
for(int j=1;j<=primesize&&i*prime[j]<=listsize;j++)
{
isprime[i*prime[j]]=false;
if(i%prime[j]==0)break;
}
}
}
欧拉函数
对于一个正整数n,小于n且和n互质的正整数(包括1)的个数,记作 φ(n) 。
欧拉函数的通式:φ(n)=n(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)……(1-1/pn)
其中p1, p2……pn为n的所有质因数,n是不为0的整数。φ(1)=1(唯一和1互质的数就是1本身)。
所有的质数的欧拉函数值都比本身小一。
φ(n)=n-1(n为质数)
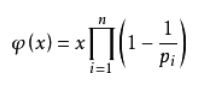
函数性质:
(1) p^k型欧拉函数:
若N是质数p(即N=p), φ(n)= φ(p)=p-p^(k-1)=p-1。
若N是质数p的k次幂(即N=pk),φ(n)=pk-p(k-1)=(p-1)p(k-1)。
(2)mn型欧拉函数
设n为正整数,以φ(n)表示不超过n且与n互素的正整数的个数,称为n的欧拉函数值。若m,n互质,φ(mn)=(m-1)(n-1)=φ(m)φ(n)。
(3)特殊性质:
若n为奇数时,φ(2n)=φ(n)。
对于任何两个互质 的正整数a,n(n>2)有:a^φ(n)=1 mod n (恒等于)此公式即 欧拉定理
当n=p 且 a与素数p互质(即:gcd(a,p)=1)则上式有: a^(p-1)=1 mod n (恒等于)此公式即 费马小定理
inline long long eular(long long n)//计算φ(n)
{
long long ans = n;
for(int i=2; i*i <= n; ++i)
{
if(n%i == 0)
{
ans = ans/i*(i-1);
while(n%i == 0)
n/=i;
}
}
if(n > 1) ans = ans/n*(n-1);
return ans;
}
输出1—n之间所有的欧拉函数值
#include<bits/stdc++.h>
using namespace std;
long long int phi[10000000];
void Euler(){
phi[1]=1;
for(long long int i=2;i<3e4;i++)
if(!phi[i])//没有被筛过说明是质数
for(long long int k=i;k<3e4;k+=i){
if(!phi[k]) phi[k]=k;
phi[k]=phi[k]/i*(i-1);//欧拉函数公式的实现
}
return ;
}
int main(){
int n;
cin>>n;
Euler();
for(int i=1;i<=n;i++)
cout<<phi[i]<<' ';
}
快速幂
首先,有这样一个公式
\((a^b)%c=((a%c)^b)%c\)
\((a*b)%c=((a%c)*(b%c))%c\)
长得好奇怪。。但其实和实数运算法则一样。。
这样就有下面的第一步优化,为了使求出来的值不超long long
int ans = 1;
a = a % c; //加上这一句
for(int i = 1;i<=b;i++)ans = ans * a;
ans = ans % c;
(但是这样也还是会超。。)
再看一下上面的公式,既然先相乘再取余与先取余再相乘再取余一样,那就可以给每一步的结果ans取余。
int ans = 1;
a = a % c;
for(int i = 1;i<=b;i++)ans = (ans * a) % c;//这里再取了一次余
ans = ans % c;
这时的时间复杂度为O(b)
虽然现在不会溢出,但是当b很大的时候还是会超时
然后,有这样一个公式
ab%c==((a2)b/2)%c == ((a^2 % c)b/2)%c b为偶数
ab%c==(a*(a2)b/2)%c == (a*(a^2 % c)b/2)%c b为奇数
这样,就可以进一步优化为:
int ans = 1;
a = a % c;
k = (a*a) % c; //相当于用k代替了a2
if(b%2==1)
ans = (ans * a) % c; //如果是奇数,要多求一步,可以提前算到ans中
for(int i = 1;i<=b/2;i++) ans = (ans * k) % c;
ans = ans % c;
这时的时间复杂度是O(b/2)
还是远远不够啊。。
但是,由上面的一次优化可以发现,我们已经把ab%c转换成了k(b/2)%c
而K^(b/2)%c是可以继续迭代下去的
例如,
下一步再令 \(x=(k*k)%c 偶数就是求 x^b/4 % c 奇数就是 (x^b/4 % c*a)% c\)
再下一步令 \(y=(x*x)%c 偶数就是求 y^b/8 % c 奇数就是 (y^b/8 % c*a)% c\)
\(...... 直到指数b ==0\)
当然,对于奇数的情形会多出一项a % c,所以为了完成迭代,当b是奇数时,我们通过ans = (ans * a) % c; 来弥补多出来的这一项
int ans = 1;
a = a % c;
while(b>0)
{
if(b % 2 == 1)ans = (ans * a) % c; //奇数,补一项
b = b/2;
a = (a * a) % c;
}
cout<<ans<<endl;
这时的时间复杂度是O(logb)
就是完整的快速幂算法!
#include<iostream>
#include<cstdio>
using namespace std;
long long int a,b,c;
long long int ans=1,bent;
int main()
{
scanf("%d%d%d",&a,&b,&c);
bent=a;
while(b)
{
if(b&1)
ans=(ans*bent)%c;
bent=(bent*bent)%c;
b/=2;
}
printf("%d",ans);
return 0;
}
最终版本
int power(int a,int n){
int tp=1;
while(n){
if(n&1)tp=1ll*tp*a%mod;
a=1ll*a*a%mod,
n>>=1;
}
return tp;
}
扩展欧几里得算法
扩展欧几里得算法是欧几里得算法(又叫辗转相除法)的扩展。除了计算a、b两个整数的最大公约数,此算法还能找到整数x、y(其中一个很可能是负数)。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数——这是众所周知的。然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。
给定 n 对正整数 ai,bi,对于每对数,求出一组 xi,yi,使
其满足 ai*xi+bi*yi=gcd(ai,bi)。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 ai,bi。
输出格式
输出共 n 行,对于每组 ai,bi,求出一组满足条件的 xi,yi,每组结果占一行。
本题答案不唯一,输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤105,
1≤ai,bi≤2×109
输入样例:
2
4 6
8 18
输出样例:
-1 1
-2 1
#include <iostream>
#include <algorithm>
using namespace std;
int exgcd(int a, int b, int &x, int &y)
//求 ax + by = c 的一组解
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
int x, y;
exgcd(a, b, x, y);
printf("%d %d\n", x, y);
}
return 0;
}
给定 n 组数据 ai,bi,mi,对于每组数求出一个 xi,使其满足 ai×xi≡bi(modmi),如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组数据 ai,bi,mi。
输出格式
输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105,
1≤ai,bi,mi≤2×109
输入样例:
2
2 3 6
4 3 5
输出样例:
impossible
-3
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, b, m;
scanf("%d%d%d", &a, &b, &m);
int x, y;
int d = exgcd(a, m, x, y);
if (b % d) puts("impossible");
else printf("%d\n", (LL)b / d * x % m);
}
return 0;
}
中国剩余定理
这玩意太变态了,随便一个模板都是紫题,我就直接粘几道题算了。
中国剩余定理
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn,求一
个最小的非负整数 x,满足 ∀i∈[1,n],x≡mi(mod
ai)。
输入格式
第 1 行包含整数 n。
第 2…n+1 行:每 i+1 行包含两个整数 ai 和 mi,
数之间用空格隔开。
输出格式
输出最小非负整数 x,如果 x 不存在,则输出 −1。
如果存在 x,则数据保证 x 一定在 64 位整数范围内。
数据范围
1≤ai≤2^31−1,
0≤mi<ai
1≤n≤25
输入样例:
2
8 7
11 9
输出样例:
31
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
int n;
cin >> n;
LL x = 0, m1, a1;
cin >> m1 >> a1;
for (int i = 0; i < n - 1; i ++ )
{
LL m2, a2;
cin >> m2 >> a2;
LL k1, k2;
LL d = exgcd(m1, m2, k1, k2);
if ((a2 - a1) % d)
{
x = -1;
break;
}
k1 *= (a2 - a1) / d;
k1 = (k1 % (m2/d) + m2/d) % (m2/d);
x = k1 * m1 + a1;
LL m = abs(m1 / d * m2);
a1 = k1 * m1 + a1;
m1 = m;
}
if (x != -1) x = (a1 % m1 + m1) % m1;
cout << x << endl;
return 0;
}
扩展中国剩余定理
给定 n 组非负整数 ai, bi,求解关于 x 的方程组的最小
非负整数解。
x ≡ b1 (mod a1)
x ≡ b2 (mod a2)
.......
x ≡ bn (mod an)
输入格式
输入第一行包含整数 n。
接下来 nn 行,每行两个非负整数 ai, bi
输出格式
输出一行,为满足条件的最小非负整数 x。
输入样例
3
11 6
25 9
33 17
输出样例
809
#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long lt;
lt read()
{
lt f=1,x=0;
char ss=getchar();
while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
return f*x;
}
const int maxn=100010;
int n;
lt ai[maxn],bi[maxn];
lt mul(lt a,lt b,lt mod)
{
lt res=0;
while(b>0)
{
if(b&1) res=(res+a)%mod;
a=(a+a)%mod;
b>>=1;
}
return res;
}
lt exgcd(lt a,lt b,lt &x,lt &y)
{
if(b==0){x=1;y=0;return a;}
lt gcd=exgcd(b,a%b,x,y);
lt tp=x;
x=y; y=tp-a/b*y;
return gcd;
}
lt excrt()
{
lt x,y,k;
lt M=bi[1],ans=ai[1];//第一个方程的解特判
for(int i=2;i<=n;i++)
{
lt a=M,b=bi[i],c=(ai[i]-ans%b+b)%b;//ax≡c(mod b)
lt gcd=exgcd(a,b,x,y),bg=b/gcd;
if(c%gcd!=0) return -1; //判断是否无解,然而这题其实不用
x=mul(x,c/gcd,bg);
ans+=x*M;//更新前k个方程组的答案
M*=bg;//M为前k个m的lcm
ans=(ans%M+M)%M;
}
return (ans%M+M)%M;
}
int main()
{
n=read();
for(int i=1;i<=n;++i)
bi[i]=read(),ai[i]=read();
printf("%lld",excrt());
return 0;
}
范德蒙德卷积
\(范德蒙卷积公式:\)
\(对于所有的正整数(m_1,m_2,n\),有\)
\([\sum_{k = 0}^n\dbinom{m_1}{k}\dbinom{m_2}{n - k} = \dbinom{m_1+m_2}{n}\]\)
\(首先考虑(\dbinom{m_1+m_2}{n}\)的组合意义:\)
\(大小为(|m_1 + m_2|\)的集合中选择大小为(|n|\)的集合的个数.\)
\(我们将其中(m_1\)个元素涂上A颜色,剩下的元素涂上B颜色.(A集合包含了所有颜色为A的元素,B集合同理)\)
\(然后将(|n|\)子集分为n+1类\)
\((|C_0| , |C_1| , |C_2|...|C_n|\)\)
\((C_k\)表示k个A颜色,n - k个B颜色的(|n|\)子集个数.\)
\(那么就有\)
\(\[\dbinom{m_1+m_2}{n} = \sum_{i = 0}^n{|C_i|}\]\)
\(考虑如何计算\(C_k\).\)
\(因为有K个A颜色,n - k个B颜色,所以相当于,从A集合中选择K个元素,从B集合选择n - k个元素\)
\(所以就有\(|C_k| = \dbinom{m_1}{k}\dbinom{m_2}{n - k}\)\)
\(带入到上面的式子就成为\)
\(\[\dbinom{m_1+m_2}{n} = \sum_{i = 0}^n{\dbinom{m_1}{i}\dbinom{m_2}{n - i}}\]\)
隔板法
隔板法就是在n个元素间的(n-1)个空插入k-1个板子,把n个元素分成k组的方法。
应用隔板法必须满足的3个条件:
n个元素是相同的
k个组是互异的
每组至少分得一个元素
公式
将n个相同的求放到m个不同的盒子里的个数为:\(Cm−1n−1\)
例如,把10个相同的球放入3个不同的箱子,每个箱子至少一个,问有几种情况? \(Cm−1n−1=C29\)
隔板法应用
普通隔板法
例1.求方程x+y+z=10的正整数解的个数。
分析:将10个求排成一排,球与球之间形成9个空隙,将两个隔板插入这些空隙中(每空至多插一块隔板),规定由隔板分成的左、中、右三部分的球数分别为x、y、z的值,则隔板法与解的个数之间建立了一一对应关系,故解的个数为C(n-1, m-1) = C(9, 2) = 36.
添元素隔板法
例2. 求方程 x+y+z=10的非负整数解的个数。
分析:注意到x、y、z可以为零,故例1解法中的限定“每空至多插一块隔板”就不成立了,怎么办呢?只要添加三个球,给x、y、z各添加一个球,这样原问题就转化为求 x+y+z=13的正整数解的个数了,则问题就等价于把13个相同小球放入3个不同箱子,每个箱子至少一个,有几种情况?易得解的个数为C(n+m-1,m-1)=C(12,2)=66(个)。
例3.把10个相同的小球放到3个不同的箱子,第一个箱子至少1个,第二个箱子至少3个,第3个箱子可以为空,有几种情况?
我们可以在第二个箱子先放入10个小球中的2个,小球剩8个放3个箱子,然后在第三个箱子放入8个小球之外的1个小球(即补充了一个球),则问题转化为把9个相同小球放3不同箱子,每箱至少1个,几种方法?C(8,2)=28
减元素隔板法
例4. 将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数。
分析:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个球,再把剩下的球分成4组,每组至少1个,由例1知方法有C(13,3)=286(种)。
添板插板法
例5.有一类自然数序列,从第三个数字开始,每个数字都恰好是它前面两个数字之和,直至不能再写为止,如1 4 5 9,5 8 13等等,这类数共有几个?
分析:因为前2位唯一确定了整个序列,只要求出前两位的所有情况即可,设前两位为a和b
显然a + b <= 9,且a不为0.
设1代表9个1,_代表8个空位.
我们要把9分成两组,但b可以为0,我们先给b一个1,然后就相当于把10个球放入(a, b)两不同的盒子里,每个盒子至少放一个,C(9, 1),但这是错误的,为什么?因为1不一定要全部放入。其实解决这个问题可以这么想,我们引入一个盒子c放a、b取完后剩下的1,所以保证c中球数大于0,需要再增加一个球,题目等价于,11个球放入3个不同的箱子,每个箱子至少放一个,C(10, 2).
例5另一种解法:
显然a + b <= 9,且a不为0.
设1代表9个1,代表8个空位.
之前我们可以在9个空位中插入2个板,分成3组,第一组取到a个1,第二组取到b个1,但此时第二组始终不能取空。若在末尾添加两个空,第二组就能取到空,所以共有C(10, 2).
选板法
例6.有10粒糖,如果每天至少吃一粒(多不限),吃完为止,求有多少种不同吃法?
分析:o代表10个糖,_ 代表9个空,所以10块糖,9个空,插入9块隔板,每个板都可以选择放或不放,相邻两板间的糖一天吃掉,这样共有
2^9=512啦.
分类插板法
例7.小梅有15块糖,如果每天至少吃3块,吃完为止,那么共有多少种不同的吃法?
分析:
此问题不能用插板法的原因在于没有规定一定要吃几天,因此我们需要对吃的天数进行分类讨论
最多吃5天,最少吃1天
1: 吃1天或是5天,各一种吃法 一共2种情况
2:吃2天,每天预先吃2块,即问11块糖,每天至少吃1块,吃2天,几种情况? C(10, 1)=10
3:吃3天,每天预先吃2块,即问9块糖,每天至少1块,吃3天? C(8 ,2)=28
4:吃4天,每天预先吃2块,即问7块糖,每天至少1块,吃4天?c(6 ,3)=20
所以一共是 2+10+28+20=60 种 .
逐步插板法
我觉得叫逐步插空法更好,为什么?看例题
例8.在一张节目单中原有6个节目,若保持这些节目相对次序不变,再添加3个节目,共有几种情况?
分析:可以用一个节目去插7个空位,再用第二个节目去插8个空位,用最后个节目去插9个空位,所以一共是C(7, 1)×C(8, 1)×C(9, 1)=504种.
杨辉三角
杨辉三角(欧洲叫帕斯卡三角)是一个很奇妙的东西,它是我国数学家杨辉在1261年发现的,欧洲的帕斯卡于1654年发现,比我国的巨佬数学家杨辉晚了393年。(在此show一下我的爱国情怀)
铺垫知识
(1)二项式系数
二项式系数,定义为(1+x)n展开之后x的系数。
通常来讲,二项式系数代表的是从n件物品中,无序地选取k件的方法总数,如果你读过我全排列的博客链接,那么你会发现,这就是我们定义的“组合数”。
证明也比较简单:
我们假设上述的n=4,k=2,通过组合数公式可以得出组合数为6.
假如我们把\((1+x)4\)展开并标记每一个x,就会得到:
\((1+x1)(1+x2)(1+x3)(1+x4)\)
上式等于:
\((1+x1)⋯(1+x4)=⋯+x1x2+x1x3+x1x4+x2x3+x2x4+x3x4+⋯\)
我们发现,假如把标记去掉,这个x2的系数正好等于6.
也就证明了:\((1+x)n\)中\(xk\)的系数正好等于从n个元素中选取k个元素的组合数\((Ckn)\).
杨辉三角性质
杨辉三角(帕斯卡三角),是二项式系数在三角形中的几何排列。我们看一发杨辉三角的图,并在此图上进行后续的讲解
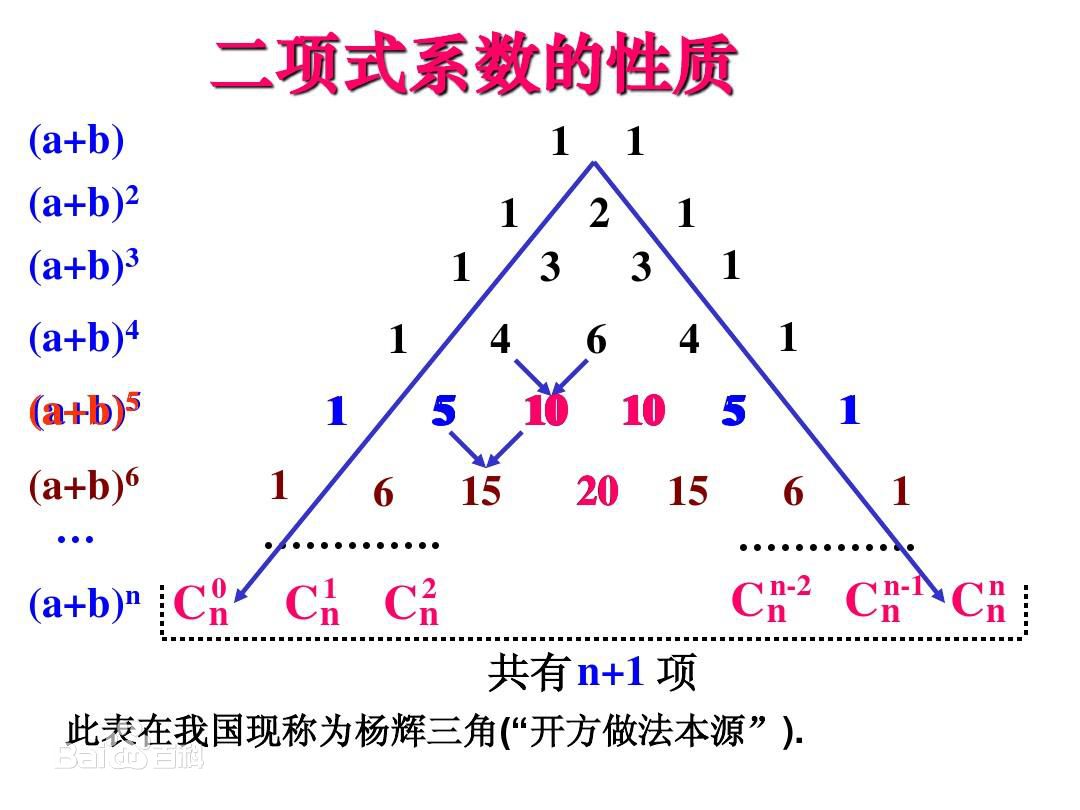
我们从这张杨辉三角示意图上发现,杨辉三角的每行行首与每行结尾的数都为1.而且,每个数等于其左上及其右上二数的和。这样我们发现,杨辉三角左右对称。
那么我们就可以通过这些基本概念把这个杨辉三角同我们所说的组合数即二项式系数联系在一起:
通过刚才的知识铺垫,我们发现,第i行的第j个数,我们可以用Cji来表示从i个元素中选取j个元素的组合数。(注意,这里的第i行是从0计数)并且,由于对称性,我们可以发现,杨辉三角中第n行的第m个数恒等于本行的第n-m+1个数。
与二项式系数知识点进行结合,我们会发现(1+x)n展开后,各次数的系数正好对应第n行的每一项。
杨辉三角代码实现的递推公式
在很多题目中,我们常常需要用打表的形式先处理出杨辉三角矩阵,然后再以此为基础进行程序求解。那么我们打表的时候如果手存表格的话,不仅浪费考试时间,而且保证不了空间范围和正确性,这个时候需要我们使用递推的手段用程序处理出表格。
根据杨辉三角的性质,我们推出以下的递推公式:(如果看完了上面这些,这个还看不懂的话,就退役吧)
C[i][j]=C[i−1][j]+C[i−1][j−1];
杨辉三角的基本知识点大约是这个样子。
高斯消元
这玩意同样也很恶心,我就直接记记原理算了。
1.把某一个方程的两边同乘一个非零的数
2.交换某两个方程的位置
3.把某行的若干倍加到另一行上
代码实现:
输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例:
\(a_{11}x_1+a_{12}x_2+......a_{1n}+x_n=b_1\)
\(a_{21}x_1+a_{22}x_2+......a_{1n}+x_n=b_2\)
……………………
\(a_{m1}x_1+a_{m2}x_2+......a_{mn}+x_n=b_m\)
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个实数,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出 Infinite group solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数,绝对值均不超过 100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 110;
const double eps = 1e-8;
int n;
double a[N][N];
int gauss() // 高斯消元,答案存于a[i][n]中,0 <= i < n
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ ) // 找绝对值最大的行
if (fabs(a[i][c]) > fabs(a[t][c]))
t = i;
if (fabs(a[t][c]) < eps) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]); // 将绝对值最大的行换到最顶端
for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c]; // 将当前行的首位变成1
for (int i = r + 1; i < n; i ++ ) // 用当前行将下面所有的列消成0
if (fabs(a[i][c]) > eps)
for (int j = n; j >= c; j -- )
a[i][j] -= a[r][j] * a[i][c];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; i ++ )
if (fabs(a[i][n]) > eps)
return 2; // 无解
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] -= a[i][j] * a[j][n];
return 0; // 有唯一解
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n + 1; j ++ )
scanf("%lf", &a[i][j]);
int t = gauss();
if (t == 2) puts("No solution");
else if (t == 1) puts("Infinite group solutions");
else
{
for (int i = 0; i < n; i ++ )
{
if (fabs(a[i][n]) < eps) a[i][n] = 0; // 去掉输出 -0.00 的情况
printf("%.2lf\n", a[i][n]);
}
}
return 0;
}
输入一个包含 n 个方程 n 个未知数的异或线性方程组。
方程组中的系数和常数为 0 或 1,每个未知数的取值也为 0 或 1。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR),M[i][j] 表示第 i 个式子中 x[j] 的系数,B[i] 是第 i 个方程右端的常数,取值均为 0 或 1。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n+1 个整数 0 或 1,表示一个方程的 n 个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共 n 行,其中第 i 行输出第 i 个未知数的解。
如果给定线性方程组存在多组解,则输出 Multiple sets of solutions。
如果给定线性方程组无解,则输出 No solution。
数据范围
1≤n≤100
输入样例:
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例:
1
0
0
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n;
int a[N][N];
int gauss()
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ )
if (a[i][c])
t = i;
if (!a[t][c]) continue;
for (int i = c; i <= n; i ++ ) swap(a[r][i], a[t][i]);
for (int i = r + 1; i < n; i ++ )
if (a[i][c])
for (int j = n; j >= c; j -- )
a[i][j] ^= a[r][j];
r ++ ;
}
if (r < n)
{
for (int i = r; i < n; i ++ )
if (a[i][n])
return 2;
return 1;
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] ^= a[i][j] * a[j][n];
return 0;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n + 1; j ++ )
cin >> a[i][j];
int t = gauss();
if (t == 0)
{
for (int i = 0; i < n; i ++ ) cout << a[i][n] << endl;
}
else if (t == 1) puts("Multiple sets of solutions");
else puts("No solution");
return 0;
}
组合数
要不,给个计算公式然后上几道例题???
\(C_n^m=n(n-1)......(n-m+1)/m!\)
组合数的计算说实话,水.........我就不写了。
卢卡斯定理
求\(C_{n+m}^n mod\) \(p\),p为质数,其中 C 为组合数。
输入格式
第一行一个整数 T,表示数据组数。
对于每组数据:
一行,三个整数 n, m, p。
输出格式
对于每组数据,输出一行,一个整数,表示所求的值。
#include<iostream>
#include<algorithm>
#include<cstdio>
#define ed 100005
using namespace std;
int k,n,m,p;
long long a[ed],b[ed];
long long lucas(int x,int y)
{
if(x<y) return 0;
else if(x<p) return b[x]*a[y]*a[x-y]%p;
else return lucas(x/p,y/p)*lucas(x%p,y%p)%p;
}
int main()
{
scanf("%d",&k);
while(k)
{
scanf("%d%d%d",&n,&m,&p);
a[0]=a[1]=b[0]=b[1]=1;
for(int i=2;i<=n+m;i++) b[i]=b[i-1]*i%p;
for(int i=2;i<=n+m;i++) a[i]=(p-p/i)*a[p%i]%p;
for(int i=2;i<=n+m;i++) a[i]=a[i-1]*a[i]%p;
printf("%lld\n",lucas(n+m,m));
k--;
}
return 0;
}
第二种计算方式:
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = 1, j = a; i <= b; i ++, j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
扩展卢卡斯定理
求\(C_n^m mod\) \(p\),其中 C 为组合数。
输入格式
一行三个整数 n,m,p含义由题所述。
输出格式
一行一个整数,表示答案。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define int long long
using namespace std;
const int MAXN=1000010;
inline int qpow(int x,int k,int p){
int s=1;
while(k){
if(k&1) s=s*x%p;
k>>=1;
x=x*x%p;
}
return s;
}
inline int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1; y=0;
return a;
}
int t=exgcd(b,a%b,y,x);
y-=a/b*x;
return t;
}
inline int mod_fact(int n,int &e,int p,int MOD){
if(!n) return 1;
int res=1;
for(int i=2;i<=MOD;++i) //暴力累乘一个循环
if(i%p) res=res*i%MOD;
res=qpow(res,n/MOD,MOD); //共有n/MOD个循环
e+=n/p;
for(int i=2;i<=n%MOD;++i)
if(i%p) res=res*i%MOD; //乘上循环外面的数
return res*mod_fact(n/p,e,p,MOD)%MOD; //递归处理n/p个p的倍数
}
inline int C(int n,int m,int p,int MOD){
if(m>n) return 0;
int e1=0,e2=0,e3=0;
int a1=mod_fact(n,e1,p,MOD),a2=mod_fact(m,e2,p,MOD),a3=mod_fact(n-m,e3,p,MOD);
if(e1-e2-e3>0){
int temp=pow(p,e1-e2-e3);
if(temp>=MOD) return 0; //p^(e1-e2-e3)是p^ai的倍数
a1=a1*temp%MOD;
}
int x,y; exgcd(a2*a3%MOD,MOD,x,y);
return a1*x%MOD;
}
int n,m,p,a[110],b[110],cnt;
signed main()
{
scanf("%lld%lld%lld",&n,&m,&p);
int k=sqrt(p),x=p;
for(int i=2;i<=k;++i)
if(x%i==0){
int t=1;
while(x%i==0)
x/=i,t*=i;
a[++cnt]=t;
b[cnt]=C(n,m,i,t);
}
if(x!=1){
a[++cnt]=x;
b[cnt]=C(n,m,x,x);
}
int A=a[1],B=b[1];
for(int i=2;i<=cnt;++i){
int k1,k2;
int g=exgcd(A,a[i],k1,k2);
int t=A;
A=A*a[i]/g;
B=(t*k1%A*(b[i]-B)/g%A+B)%A;
}
printf("%lld\n",(B+A)%A);
return 0;
}
给定 n 个 0 和 n 个 1,它们将按照某种顺序排成长度为
2n 的序列,求它们能排列成的所有序列中,能够满足任意前
缀序列中 0 的个数都不少于 1 的个数的序列有多少个。
输出的答案对 10^9+7 取模。
输入格式
共一行,包含整数 n。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤105
输入样例:
3
输出样例:
5
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
int a = n * 2, b = n;
int res = 1;
for (int i = a; i > a - b; i -- ) res = (LL)res * i % mod;
for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;
res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
cout << res << endl;
return 0;
}
输入 a,b,求 \(C_a^b\) 的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数 a 和 b。
输出格式
共一行,输出 Cba 的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int n, int p)
{
int res = 0;
while (n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < a.size(); i ++ )
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
puts("");
return 0;
}
函数法计算组合(高精):
#include<bits/stdc++.h>
int ans[1001],a[100000][1001],m[1001],n[1001],nm[1001],ln=0,lm=0,lnm=0,w,nmm[1001],f=1,k,t;
using namespace std;
inline void zuhe(int &mm,int &nn){
int i,g=0,j;
a[0][1]=1;
for(i=1;i<=mm;i++){
g=0;
for(j=1;j<=1000;j++){
a[i][j]=a[i-1][j]*i+g;
g=a[i][j]/10;
a[i][j]=a[i][j]%10;
}
}
for(i=1;i<=1000;i++)
{
m[i]=a[mm][i];
if(m[i]>0) lm=i;
n[i]=a[nn][i];
if(n[i]>0) ln=i;
nm[i]=a[mm-nn][i];
if(nm[i]>0) lnm=i;
}
g = 0;
for(i=1;i<=lnm+1;i++)
{
for(j=1;j<=ln+1;j++)
{
w=i+j-1;
nmm[w]=nmm[w]+nm[i]*n[j]+g;
g=nmm[w]/10;
nmm[w]=nmm[w]%10;
}
}
while(f==1)
{
for(i=1;i<=lm;i++)
{
m[i]=m[i]-nmm[i];
if(m[i]<0)
{
m[i+1]=m[i+1]-1;
m[i]=m[i]+10;
}
}
k=1;
while(ans[k]==9)
{
ans[k]=0;
k++;
}
ans[k]++;
f=0;
for(i=1;i<=lm;i++) if(m[i]>0) f=1;
}
k=1000;
while(ans[k]==0) k--;
if(k>5) t=k+1-5; else t=1;
nn=t,mm=k;
return ;
}
int main(){
//先输入大的,再输入小的
int a,b;
cin>>a>>b;
zuhe(a,b);
for(int i=b;i>=a;i--) cout<<ans[i];
}
容斥原理
对容斥原理的描述
容斥原理是一种重要的组合数学方法,可以让你求解任意大小的集合,或者计算复合事件的概率。
容斥原理可以描述如下:
要计算几个集合并集的大小,我们要先将所有单个集合的大小计算出来,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推,一直计算到所有集合相交的部分。
关于集合的原理公式
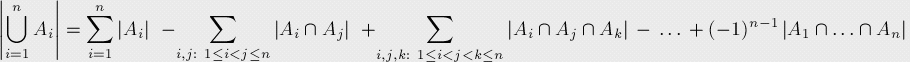
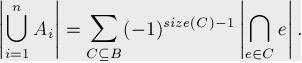
关于维恩图的原理
用维恩图来表示集合A、B和C:
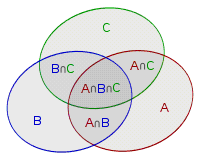
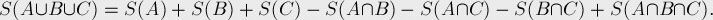
关于概率论的原理
设事件,代表发生某些事件的概率(即发生其中至少一个事件的概率),则:
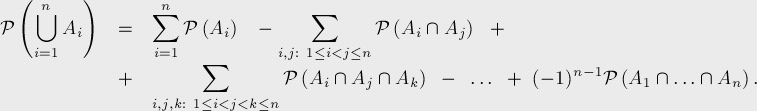
这个公式也可以用B代表Ai的集合:
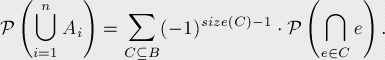
代码实现
给定一个整数 n 和 m 个不同的质数 p1,p2,…,pm。
请你求出 1∼n 中能被 p1,p2,…,pm 中的至少一个数整除的
整数有多少个。
输入格式
第一行包含整数 n 和 m。
第二行包含 m 个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
数据范围
1≤m≤16,
1≤n,pi≤109
输入样例:
10 2
2 3
输出样例:
7
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
int p[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i ++ ) cin >> p[i];
int res = 0;
for (int i = 1; i < 1 << m; i ++ )
{
int t = 1, s = 0;
for (int j = 0; j < m; j ++ )
if (i >> j & 1)
{
if ((LL)t * p[j] > n)
{
t = -1;
break;
}
t *= p[j];
s ++ ;
}
if (t != -1)
{
if (s % 2) res += n / t;
else res -= n / t;
}
}
cout << res << endl;
return 0;
}
博弈论
一、巴什博弈(Bash Game)
int Bash_Game(int n,int m)//是否先手有必赢策略
{
if (n%(m+1)!=0) return 1;
return 0;
}
二、尼姆博弈(Nimm Game)
int Nimm_Game(int n)//假设n个数存在数组f[]中,有必胜策略返回1
{
int flag=0;
for(int i=1;i<=n;i++)
flag^=f[i];
if(flag) return 1;
return 0;
}
三、威佐夫博奕(Wythoff Game)
int Wythoff_Game(int a,int b)
{
if(a>b)
swap(a,b);
double x=(sqrt(5.0)-1.0)/2.0;
int k=ceil(1.0*a*x);
if(a+k==b)
return 0;//奇异局势,后手胜!
else
return 1;//非奇异局势,先手胜!
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号